hdu 6069 Counting Divisors (唯一正整数分解定理+素数筛)

题意：定义d(x)是数字x正因子的个数，给你l,r,k,求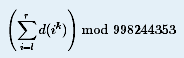

思路：任何一个大于1的自然数，都可以唯一分解成有限个质数的乘积，这里均为质数，其诸指数是正整数。那么它的正因数个数为，那么 ，由于​k​​)=(kc​1​​+1)(kc​2​​+1)...(kc​m​​+1)。l 和 r 的是到10的12次方，一个非质数肯定能由 √r 以下的质数表示出来，所以我们可以将0~10^6的素数筛出来，枚举 2~√r 的所有素数p，再枚举区间[l,r]中所有p的倍数，将其分解质因数，如果最后剩下的数大于1说明是大于√r的质数

代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#define ll long long

using namespace std;

const ll mod = 998244353;
const int maxn = 1e6+10;
bool isprime[maxn];
ll prime[maxn];
ll data[maxn];
ll fac[maxn];
int tot;

void get_prime()
{
    memset(isprime,true,sizeof(isprime));
    tot=0;
    for(ll i=2;i<maxn;i++)
    {
        if(isprime[i])
        {
            prime[tot++]=i;
            for(ll j=i*i;j<maxn;j+=i)
            {
                isprime[j]=false;
            }
        }
    }
}

int main()
{
    get_prime();
    int t;
    cin>>t;
    while(t--)
    {
        ll l,r,k;
        cin>>l>>r>>k;
        for(ll i=0;i<(r-l+1);i++)
        {
            data[i]=i+l;
            fac[i]=1;
        }
        for(int i=0;i<tot&&prime[i]*prime[i]<=r;i++)
        {
            ll p=l-l%prime[i];
            if(p<l) p=p+prime[i];
            for(ll j=p;j<=r;j=j+prime[i])
            {
                ll cnt=0;
                ll wei=j-l;
                while(data[wei]%prime[i]==0)
                {
                    cnt++;
                    data[wei]=data[wei]/prime[i];
                }
                fac[wei]=(fac[wei]*(cnt*k%mod+1))%mod;
            }
        }
        ll ans=0;
        for(int i=0;i<(r-l+1);i++)
        {
            if(data[i]>1) fac[i]=fac[i]*(k+1)%mod;
            ans=(ans+fac[i])%mod;
        }
        cout<<ans<<endl;
    }
}

(∑i=lrd(ik))mod99824435

(∑i=lrd(ik))mod9982443

(∑i=lrd(ik))mod998244353