A. Distance and Axis (codeforces1401A) (数学+思维）

A. Distance and Axis

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

We have a point AA with coordinate x=nx=n on OXOX-axis. We'd like to find an integer point BB (also on OXOX-axis), such that the absolute difference between the distance from OO to BB and the distance from AA to BB is equal to kk.

The description of the first test case.

Since sometimes it's impossible to find such point BB, we can, in one step, increase or decrease the coordinate of AA by 11. What is the minimum number of steps we should do to make such point BB exist?

Input

The first line contains one integer tt (1≤t≤60001≤t≤6000) — the number of test cases.

The only line of each test case contains two integers nn and kk (0≤n,k≤1060≤n,k≤106) — the initial position of point AA and desirable absolute difference.

Output

For each test case, print the minimum number of steps to make point BB exist.

Example

input

Copy

6
4 0
5 8
0 1000000
0 0
1 0
1000000 1000000

output

Copy

0
3
1000000
0
1
0

Note

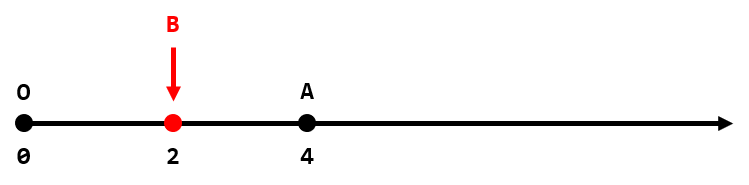
In the first test case (picture above), if we set the coordinate of BB as 22 then the absolute difference will be equal to |(2−0)−(4−2)|=0|(2−0)−(4−2)|=0 and we don't have to move AA. So the answer is 00.

In the second test case, we can increase the coordinate of AA by 33 and set the coordinate of BB as 00 or 88. The absolute difference will be equal to |8−0|=8|8−0|=8, so the answer is 33.

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define scanf scanf_s

int T;
int n, k;

int main() {
    cin >> T;
    while (T--) {
        scanf("%d%d", &n, &k);
        //(Xa-Xb)-Xb = k     ==> xb = (k-xa)/2 //B在OA之间 //需要判断奇偶
        // Xb - (Xb-Xa) = k  ==> Xa = k // B在A的右边 // 此时a的左边由n变化到k

    
        if (k > n) {
            printf("%d
", k - n);
        }
        else {
            if ((n - k) % 2 == 0) {
                printf("%d
", 0);
            }
            else if ((n - k) % 2 == 1) {
                printf("%d
", 1);
            }
        }
    }

    return 0;
}