CodeForces

先上题目：

E. Pashmak and Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Pashmak's homework is a problem about graphs. Although he always tries to do his homework completely, he can't solve this problem. As you know, he's really weak at graph theory; so try to help him in solving the problem.

You are given a weighted directed graph with n vertices and m edges. You need to find a path (perhaps, non-simple) with maximum number of edges, such that the weights of the edges increase along the path. In other words, each edge of the path must have strictly greater weight than the previous edge in the path.

Help Pashmak, print the number of edges in the required path.

Input

The first line contains two integers n, m (2 ≤ n ≤ 3·105; 1 ≤ m ≤ min(n·(n - 1), 3·105)). Then, m lines follows. The i-th line contains three space separated integers: ui, vi, wi (1 ≤ ui, vi ≤ n; 1 ≤ wi ≤ 105) which indicates that there's a directed edge with weight wi from vertex ui to vertex vi.

It's guaranteed that the graph doesn't contain self-loops and multiple edges.

Output

Print a single integer — the answer to the problem.

Sample test(s)

input

3 3
1 2 1
2 3 1
3 1 1

output

1

input

3 3
1 2 1
2 3 2
3 1 3

output

3

input

6 7
1 2 1
3 2 5
2 4 2
2 5 2
2 6 9
5 4 3
4 3 4

output

6

Note

In the first sample the maximum trail can be any of this trails: .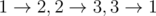

In the second sample the maximum trail is .

In the third sample the maximum trail is .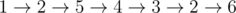

　　题意：给你一个有向图，问你最长的路径有多长，这条最长路径需要满足每一小段都要比前面的那一小段严格大。

　　做法：经过分析，我们可以发现需要先贪心一下，先从权值比较小的边开始计算，然后再进行dp，转移方程是dp[v]=max(dp[u]+1,dp[v])，u是起点,v是终点，dp[k]保存以k为终点的路径的最长长度。这里需要处理一下权值相等的情况保证他们不会干扰就可以了。这里用的方法是借鉴别人的代码的，对于长度相同的边，我们先记录下排除长度长度相同的边得等到的最大值，然后在赋值给dp[k]。

上代码：

#include <bits/stdc++.h>
#define MAX 300002
#define ll long long
using namespace std;

typedef struct edge{
    ll u,v,w;

    bool operator < (const edge& o)const{
        return w<o.w;
    }
}edge;
edge e[MAX];
int n,m,maxn;
int dp[MAX],f[MAX];

int main()
{
    //freopen("data.txt","r",stdin);
    ios::sync_with_stdio(false);
    while(cin>>n>>m){
        memset(dp,0,sizeof(dp));
        memset(f,0,sizeof(f));
        for(int i=0;i<m;i++){
            cin>>e[i].u>>e[i].v>>e[i].w;
        }
        sort(e,e+m);
        maxn=0;
        for(int i=0;i<m;i++){
            int j;
            for(j=i;j<m;j++) if(e[i].w!=e[j].w) break;
            for(int k=i;k<j;k++){
                f[e[k].v]=max(dp[e[k].u]+1,f[e[k].v]);
            }
            for(int k=i;k<j;k++){
                dp[e[k].v]=max(f[e[k].v],dp[e[k].v]);
            }
            i=j-1;
        }
        for(int i=1;i<=n;i++) maxn=max(dp[i],maxn);
        cout<<maxn<<endl;
    }
    return 0;
}