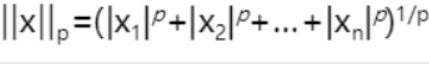python 数据分析--数值计算工具Numpy

说明：本文只做Numpy的学习记录
参考内容：
（1）微信公众号：数据分析--1480 https://mp.weixin.qq.com/s/54fQScsNn9Sg-G02CEoaOw
（2）从零开始学Python数据分析与挖掘／刘顺祥著．—北京：清华大学出版社，2018
（3）从零开始学Python数据分析（视频教学版）作者：罗攀 出版社：机械工业出版社 出版时间：2018-07

1. 使用numpy构建数组和矩阵

1.1 创建数组或矩阵

import numpy as np

# 单个列表或元组创建一维数组
arr1 = np.array([1,2.5,3.2,4.1])
print(arr1)

arr2 = np.array((10,20,30,40,50))
print(arr2)

# 创建3x3的二维矩阵
arr3 = np.array([[0,1,2,3],[4,5,6,7],[8,9,10,11]])
print(arr3)

# 查看数组和矩阵维度
print(arr1.shape)
print(arr2.shape)
print(arr3.shape)

# 查看数组的数据类型
print(arr1.dtype)
print(arr2.dtype)
print(arr3.dtype)

[1.  2.5 3.2 4.1]
[10 20 30 40 50]
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(4,)
(5,)
(3, 4)
float64
int32
int32

1.2 获取元素

使用索引的方式获取元素，一维数组和元组列表类似，在二维数组中，位置索引必须写成[rows,cols]的形式，方括号的前半部分用于控制二维数组的行索引，后半部分用于控制数组的列索引。

# 获取一维数组元素
print(arr1[0])

# 获取二维数组中的第1,2行元素
print(arr3[[0,1],:],'
') 

#获取二维数组第2,3,4列元素
print(arr3[:,[1,2,3]],'
')

#第1行第3个和第3行第4个
print(arr3[[0,2],[2,3]],'
')  

#获取某几行某几列元素
print(arr3[[0,2],:][:,[2,3]],'
') #第1行3,4列和第3行3,4列

#上面的操作可以使用np.ix_函数替换
print(arr3[np.ix_([0,2],[2,3])],'
')

1.0
[[0 1 2 3]
 [4 5 6 7]] 

[[ 1  2  3]
 [ 5  6  7]
 [ 9 10 11]] 

[ 2 11] 

[[ 2  3]
 [10 11]] 

[[ 2  3]
 [10 11]] 

1.3 数据的存储和加载

1.3.1 数据的存储

通过使用numpy模块中的savetxt函数实现python数据的写出，函数语法如下：
np.savetxt(fname, X, fmt='%.18e', delimiter=' ', newline=' ', header='', footer='', comments='# ')

fname= r'E:/Data/2/npsavetxt.csv'
arr  = np.arange(12).reshape(4,3)
np.savetxt(fname, arr, delimiter=',')

1.3.2 数据加载

numpy模块还提供了读取数据与写数据的函数，方便我们将外部数据文件读入到Python的工作环境中。这里推荐两个读数据的函数：

#读入数据

arr = np.genfromtxt(fname= r'E:/Data/2/npsavetxt.csv', delimiter=',')
arr2 = np.loadtxt(fname= r'E:/Data/2/npsavetxt.csv', delimiter=',')

print(arr)
print(arr2)

[[ 0.  1.  2.]
 [ 3.  4.  5.]
 [ 6.  7.  8.]
 [ 9. 10. 11.]]
[[ 0.  1.  2.]
 [ 3.  4.  5.]
 [ 6.  7.  8.]
 [ 9. 10. 11.]]

fname：指定外部文件的路径
delimiter：指定文件中数据列的分隔符
skiprows：指定读数时跳过的行数
skip_header：指定跳过首行
usecols：指定读取的数据列

1.4 改变数组的形状

数组形状处理的手段主要有reshape、resize、ravel、flatten、vstack、hstack、row_stack和colum_stack，下面通过简单的案例来解释这些“方法”或函数的区别。

# reshape 改变的是副本
print(arr3)
print(arr3.shape) #3x4 =12 12个元素可以改为2x6

print(arr3.reshape(2,6))
print(arr3.shape)
print(arr3)

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(3, 4)
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]
(3, 4)
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]

#  resize 是真正的改变
# 为了便于比较，使得操作不去改变arr3,重新创建和arr3一样数值的数arr4
# 创建3x3的二维矩阵
arr4 = np.array([[0,1,2,3],[4,5,6,7],[8,9,10,11]])
print(arr4)
print(arr4.shape)

print(arr4.resize(2,6))
print(arr4.shape) 
print(arr4)

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(3, 4)
None
(2, 6)
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]

# 多维数组降为一维数组，利用ravel、flatten和reshape三种方法均可以轻松解决：
arr5 = np.array([[1,10,100],[2,20,200],[3,30,300]])

#按行降维
print(arr5.ravel()) 
print(arr5.flatten())
print(arr5.reshape(-1))
print('
')

# 按列降维
print(arr5.ravel(order = 'F')) 
print(arr5.flatten(order = 'F'))
print(arr5.reshape(-1,order = 'F'))

[  1  10 100   2  20 200   3  30 300]
[  1  10 100   2  20 200   3  30 300]
[  1  10 100   2  20 200   3  30 300]


[  1   2   3  10  20  30 100 200 300]
[  1   2   3  10  20  30 100 200 300]
[  1   2   3  10  20  30 100 200 300]

# 通过flatten方法实现的降维返回的是复制，因为对降维后的元素做修改，并没有影响到原数组。
# 相反，ravel方法与reshape方法返回的则是视图，通过对视图的改变，是会影响到原数组。

# 更改预览值
arr5.flatten()[0] = 2000
print('flatten方法：
',arr5)
arr5.ravel()[1] = 1000
print('ravel方法：
',arr5)
arr5.reshape(-1)[2] = 3000
print('reshape方法：
',arr5)

flatten方法：
 [[   1 1000  100]
 [   2   20  200]
 [   3   30  300]]
ravel方法：
 [[   1 1000  100]
 [   2   20  200]
 [   3   30  300]]
reshape方法：
 [[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]]

#vstack用于垂直方向（纵向）的数组堆叠，其功能与row_stack函数一致，
#而hstack则用于水平方向（横向）的数组合并，其功能与colum_stack函数一致

arr6 = np.array([1,2,3])
print('vstack纵向合并数组：
',np.vstack([arr5,arr6]))
print('row_stack纵向合并数组：
',np.row_stack([arr5,arr6]))
arr7 = np.array([[5],[15],[25]])
print('hstack横向合并数组：
',np.hstack([arr5,arr7]))
print('column_stack横向合并数组：
',np.column_stack([arr5,arr7]))
print(arr5)
print('垂直方向计算数组的和：
',np.sum(arr5,axis = 0))
print('水平方向计算数组的和：
',np.sum(arr5, axis = 1))

vstack纵向合并数组：
 [[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]
 [   1    2    3]]
row_stack纵向合并数组：
 [[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]
 [   1    2    3]]
hstack横向合并数组：
 [[   1 1000 3000    5]
 [   2   20  200   15]
 [   3   30  300   25]]
column_stack横向合并数组：
 [[   1 1000 3000    5]
 [   2   20  200   15]
 [   3   30  300   25]]
[[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]]
垂直方向计算数组的和：
 [   6 1050 3500]
水平方向计算数组的和：
 [4001  222  333]

2. 数组的基本运算

2.1 四则运算

四则运算中的符号分别是“+-*/”，对应的numpy模块函数分别是np.add、np. subtract、np.multiply和np.divide

a = np.array([10,20,30,40])
b = np.array([1,2,5,10])

print("加法：
", np.add(a,b) )
print("减法：
", np.subtract(a,b))
print("乘法：
", np.multiply(a,b) )
print("除法：
", np.divide(a,b))

加法：
 [11 22 35 50]
减法：
 [ 9 18 25 30]
乘法：
 [ 10  40 150 400]
除法：
 [10. 10.  6.  4.]

2.2 求余、整除、指数运算

print("求余数：
", np.fmod(a,b))
print("整除：
", np.modf(a/b)[1])
print("指数：
", np.power(a,b) )
 

求余数：
 [0 0 0 0]
整除：
 [10. 10.  6.  4.]
指数：
 [        10        400   24300000 1073741824]

2.3 比较运算

运用比较运算符可以返回bool类型的值，即True和False。一般有两种情况会普遍使用到比较运算符，一个是从数组中查询满足条件的元素，另一个是根据判断的结果执行不同的操作。

arr7 = np.array([[1,2,10],[10,8,3],[7,6,5]])
arr8 = np.array([[2,2,2],[3,3,3],[4,4,4]])
arr9 = np.array([3,10,23,7,16,9,17,22,4,8,15])

# 取子集
print('从arr7中取出arr7大于arr8的所有元素：
',arr7[arr7>arr8])
print('从arr9中取出大于10的元素：
',arr9[arr9>10])

# 判断操作
print('将arr7中大于7的元素改成5，其余的不变：
',np.where(arr7>7,5,arr7))
print('将arr9中大于10 的元素改为1，否则改为0：
',np.where(arr9>10,1,0))

从arr7中取出arr7大于arr8的所有元素：
 [10 10  8  7  6  5]
从arr9中取出大于10的元素：
 [23 16 17 22 15]
将arr7中大于7的元素改成5，其余的不变：
 [[1 2 5]
 [5 5 3]
 [7 6 5]]
将arr9中大于10 的元素改为1，否则改为0：
 [0 0 1 0 1 0 1 1 0 0 1]

2.4 广播运算

前面所介绍的各种数学运算符都是基于相同形状的数组，当数组形状不同时，也能够进行数学运算的功能称为数组的广播。但是数组的广播功能必须遵守一定的规则：

• 各输入数组的维度可以不相等，但必须确保从右到左的对应维度值相等。
• 如果对应维度值不相等，就必须保证其中一个为1。
• 各输入数组都向其shape最长的数组看齐，shape中不足的部分都通过在前面加1补齐。

#对应位置相加，没有广播
# 各输入数组维度一致，对应维度值相等
arr10 = np.arange(12).reshape(3,4)
arr11 = np.arange(101,113).reshape(3,4)
print(arr10)
print(arr11)
print('3×4的二维矩阵运算：
',arr10 + arr11)

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
[[101 102 103 104]
 [105 106 107 108]
 [109 110 111 112]]
3×4的二维矩阵运算：
 [[101 103 105 107]
 [109 111 113 115]
 [117 119 121 123]]

# 广播第1条、各输入数组维度不一致，对应维度值相等
arr12 = np.arange(60).reshape(5,4,3)
arr10 = np.arange(12).reshape(4,3)
# print(arr10)
# print(arr12)
print('最终得到5×4×3的数组：
',arr12 + arr10)
#虽然维数不一样，但末尾的两个维度值是一样的，都是4和3，所以，结果是1个三维数组（5个二维数组）和1个两维数组的和。

最终得到5×4×3的数组：
 [[[ 0  2  4]
  [ 6  8 10]
  [12 14 16]
  [18 20 22]]

 [[12 14 16]
  [18 20 22]
  [24 26 28]
  [30 32 34]]

 [[24 26 28]
  [30 32 34]
  [36 38 40]
  [42 44 46]]

 [[36 38 40]
  [42 44 46]
  [48 50 52]
  [54 56 58]]

 [[48 50 52]
  [54 56 58]
  [60 62 64]
  [66 68 70]]]

# 广播第2条,各输入数组维度不一致，对应维度值不相等，但其中有一个为1
arr12 = np.arange(60).reshape(5,4,3) # 5个4*3 的二维矩阵
arr13 = np.arange(4).reshape(4,1)   #  4*1的一维列矩阵，加到4*3 的每列上。
# print(arr13)
# print(arr12)
print('维数不一致，维度值也不一致，但维度值至少一个为1：
',arr12 + arr13)

维数不一致，维度值也不一致，但维度值至少一个为1：
 [[[ 0  1  2]
  [ 4  5  6]
  [ 8  9 10]
  [12 13 14]]
  
 [[12 13 14]
  [16 17 18]
  [20 21 22]
  [24 25 26]]

 [[24 25 26]
  [28 29 30]
  [32 33 34]
  [36 37 38]]

 [[36 37 38]
  [40 41 42]
  [44 45 46]
  [48 49 50]]

 [[48 49 50]
  [52 53 54]
  [56 57 58]
  [60 61 62]]]

# 广播第3条, 加1补齐
arr14 = np.array([5,15,25])
# print(arr14)
# print(arr10)
print('arr14的维度自动补齐为(1,3)：
',arr10 + arr14)
# 将arr14的三个元素分别与arr10的3列元素分别相加

arr14的维度自动补齐为(1,3)：
 [[ 5 16 27]
 [ 8 19 30]
 [11 22 33]
 [14 25 36]]

3. numpy中常用的数学和统计函数

numpy模块的核心就是基于数组的运算，相比于列表或其他数据结构，数组的运算效率是最高的。在统计分析和挖掘过程中，经常会使用到numpy模块的函数。

轴的概念： 统计函数都有axis参数，该参数的目的就是在统计数组元素时需要按照不同的轴方向计算，如果axis=1，则表示按水平方向计算统计值，即计算每一行的统计值；如果axis=0，则表示按垂直方向计算统计值，即计算每一列的统计值。

arr = np.array([[1,10,100],[2,20,200],[3,30,300]])
print(arr)

print("垂直方向计算数组的和:
",np.sum(arr, axis=0))

print("水平方向计算数组的和:
",np.sum(arr, axis=1))

[[  1  10 100]
 [  2  20 200]
 [  3  30 300]]
垂直方向计算数组的和:
 [  6  60 600]
水平方向计算数组的和:
 [111 222 333]

4. 线性代数的相关计算

数据挖掘的理论背后几乎离不开有关线性代数的计算问题，如矩阵乘法、矩阵分解、行列式求解等。Numpy的子模块linalg可以解决各种线性代数相关的计算。

4.1 零、一、单位矩阵

print(np.zeros(10))
print(np.ones(10))
print(np.eye(3))

[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

4.2 行列式、矩阵乘法、对角线

arr1 = np.array([[1,2],[3,4]])
arr2 =  np.array([[1,1],[1,2]])
print("arr1 : 
",arr1)
print("arr2 : 
",arr2)

# 计算行列式
print("arr1 的行列式为：
", np.linalg.det(arr1))
print("arr2 的行列式为：
", np.linalg.det(arr2))

# 矩阵乘法
print("arr1 * arr2 : 
" , np.dot(arr1,arr2))
print("arr2 * arr1 : 
" , np.dot(arr2,arr1))

# 计算主对角线元素
print("arr1 的主对角线元素：
",np.diag(arr1))
print("arr1 的主对角线元素之和：
",np.trace(arr1))

arr1 : 
 [[1 2]
 [3 4]]
arr2 : 
 [[1 1]
 [1 2]]
arr1 的行列式为：
 -2.0000000000000004
arr2 的行列式为：
 1.0
arr1 * arr2 : 
 [[ 3  5]
 [ 7 11]]
arr2 * arr1 : 
 [[ 4  6]
 [ 7 10]]
arr1 的主对角线元素：
 [1 4]
arr1 的主对角线元素之和：
 5

4.3 转置矩阵、可逆矩阵

arr1 = np.array([[1,2],[3,4]])
arr2 =  np.array([[1,1],[1,2]])

# 转置矩阵
print("arr1 的转置矩阵为：
",np.transpose(arr1)) 

# 计算可逆矩阵(二阶主对换，副变号)
print("arr1 的可逆矩阵为：
", np.linalg.inv(arr1))
print("arr2 的可逆矩阵为：
", np.linalg.inv(arr2))

arr1 的转置矩阵为：
 [[1 3]
 [2 4]]
arr1 的可逆矩阵为：
 [[-2.   1. ]
 [ 1.5 -0.5]]
arr2 的可逆矩阵为：
 [[ 2. -1.]
 [-1.  1.]]

4.4 特征值和特征向量

# 特征值和特征向量 （Aε = λε）
arr3 =  np.array([[2,-1,-1],[0,-1,0],[0,2,1]]) 

print("arr3 的特征值和特征向量为:
", np.linalg.eig(arr3))   

arr3 的特征值和特征向量为:
 (array([ 2.,  1., -1.]), array([[ 1.        ,  0.70710678,  0.        ],
       [ 0.        ,  0.        ,  0.70710678],
       [ 0.        ,  0.70710678, -0.70710678]]))

4.5 多元一次方程求解

《九章算术》中有一题是这样描述的：今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗；问上、中、下禾实秉各几何？

# AX = b     np.linalg.solve
A = np.array([[3,2,1],[2,3,1],[1,2,3]])
b = np.array([39,34,26])
X = np.linalg.solve(A,b)
print("三元一次方程组的解为：
",X) 

三元一次方程组的解为：
 [9.25 4.25 2.75]

4.6 多元线性回归模型的解

多元线性回归模型一般用来预测连续的因变量，如根据天气状况预测游客数量、根据网站的活动页面预测支付转化率、根据城市人口的收入、教育水平、寿命等预测犯罪率等。该模型可以写成Y=Xβ+ε，其中Y为因变量，X为自变量，ε为误差项。要想根据已知的X来预测Y的话，必须得知道偏回归系数β的值。偏回归系数的求解方程，即β=(X'X)-1X’Y)。

# 计算偏回归系数
X = np.array([[1,1,4,3],[1,2,7,6],[1,2,6,6],[1,3,8,7],[1,2,5,8],[1,3,7,5],[1,6,10,12],[1,5,7,7],[1,6,3,4],[1,5,7,8]])
Y = np.array([3.2,3.8,3.7,4.3,4.4,5.2,6.7,4.8,4.2,5.1])

X_trans_X_inverse = np.linalg.inv(np.dot(np.transpose(X),X))
beta = np.dot(np.dot(X_trans_X_inverse,np.transpose(X)),Y)
print('偏回归系数为：
',beta)
print("线性回归模型为：Y = %.3f + %.3fx1 + %.3fx2 + %.3fx3" %(beta[0],beta[1],beta[2],beta[3]))

偏回归系数为：
 [1.78052227 0.24720413 0.15841148 0.13339845]
线性回归模型为：Y = 1.781 + 0.247x1 + 0.158x2 + 0.133x3

4.7 范数的计算

范数常常用来度量某个向量空间（或矩阵）中的每个向量的长度或大小，它具有三方面的约束条件，分别是非负性、齐次性和三角不等性。最常用的范数就是p范数，其公示可表示为：

# 范数的计算
arr17 = np.array([1,3,5,7,9,10,-12])
# 一范数
res1 = np.linalg.norm(arr17, ord = 1)
print('向量的一范数：
',res1)
# 二范数
res2 = np.linalg.norm(arr17, ord = 2)
print('向量的二范数：
',res2)
# 无穷范数
res3 = np.linalg.norm(arr17, ord = np.inf)
print('向量的无穷范数：
',res3)

向量的一范数：
 47.0
向量的二范数：
 20.223748416156685
向量的无穷范数：
 12.0

5. 伪随机数

numpy模块中的子模块random，包含了各种常见的随机数生成函数，如下图所示：

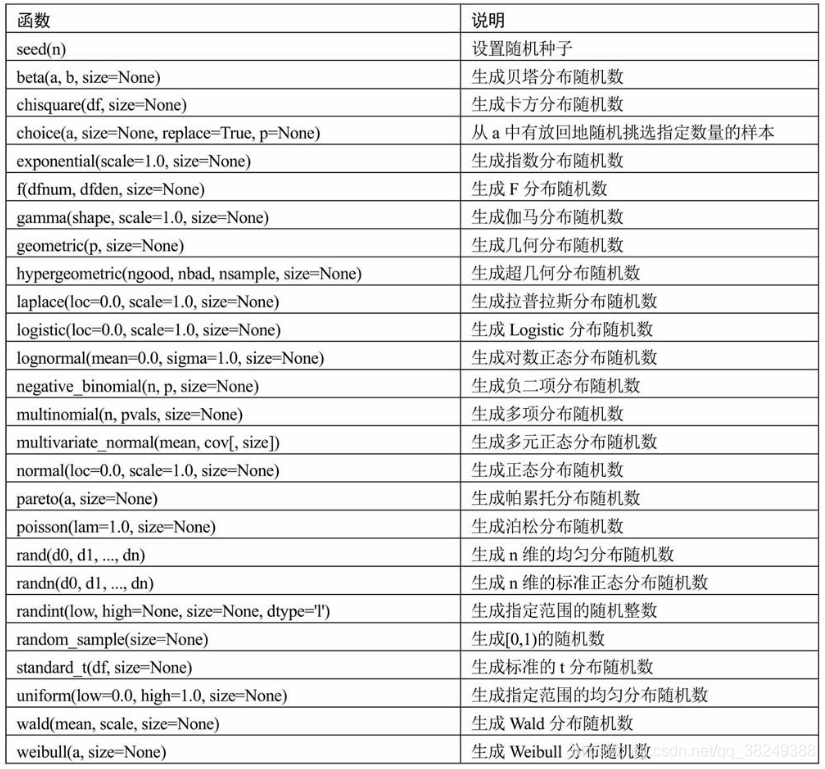
5.1 离散分布

有时候为了保证每次产生的随机数相同，就需要设置固定的随机数种子，随机数种子的设定可通过seed函数。

5.1.1 二项分布

在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。二项分布的典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率。

import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成随机数
np.random.seed(123)
 
# 二项分布
rn1 = np.random.binomial(n = 10, p= 0.2, size = 10)
rn2 = np.random.binomial(n = 10, p = 0.2, size = (3,5)) 
print(rn1)
print(rn2)
# 绘图
plt.style.use('ggplot')
sns.distplot(rn1, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'black','label':'binomial1 ','linestyle':'-'})
sns.distplot(rn2, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'red','label':'binomial2','linestyle':'--'})
# 呈现图例
plt.legend()
# 呈现图形
plt.show()

[3 1 1 2 3 2 5 3 2 2]
[[1 3 2 0 2]
 [3 1 1 2 2]
 [2 3 3 2 3]]

5.1.2 泊松分布

该分布适合于描述单位时间（或空间）内随机事件发生的次数。如某一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台的候客人数，机器出现的故障数。

import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成随机数
np.random.seed(1)
 
# 泊松分布
rn1 = np.random.poisson (lam = 6, size = 10 )
rn2 = np.random.poisson(lam = (10,50,20), size = (5,3)) 
print(rn1)
print(rn2)
# 绘图
plt.style.use('ggplot')
sns.distplot(rn1, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'black','label':'poisson1 ','linestyle':'-'})
sns.distplot(rn2, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'red','label':'poisson2','linestyle':'--'})
# 呈现图例
plt.legend()
# 呈现图形
plt.show()

[2 3 7 7 4 6 5 6 2 4]
[[11 52 13]
 [12 34 22]
 [17 61 19]
 [16 55 26]
 [12 45 22]]

5.2 连续分布

5.2.1 正太分布

正太分布也称为高斯分布，呈现两头低，中间高，左右对称的倒钟型，是连续分布中应用最频繁的一种分布。

import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成各种正态分布随机数
np.random.seed(1234)
# 正太分布（均值， 方差, 个数）
rn1 = np.random.normal(loc = 0, scale = 1, size = 1000)
rn2 = np.random.normal(loc = 0, scale = 2, size = 1000)
rn3 = np.random.normal(loc = 2, scale = 3, size = 1000)
rn4 = np.random.normal(loc = 5, scale = 3, size = 1000)
 
# 绘图
plt.style.use('ggplot')
sns.distplot(rn1, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'black','label':'u=0,s=1','linestyle':'-'})
sns.distplot(rn2, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'red','label':'u=0,s=2','linestyle':'--'})
sns.distplot(rn3, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'blue','label':'u=2,s=3','linestyle':':'})
sns.distplot(rn4, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'purple','label':'u=5,s=3','linestyle':'-.'})
# 呈现图例
plt.legend()
# 呈现图形
plt.show()

呈现的是不同均值和标准差下的正态分布概率密度曲线。当均值相同时，标准差越大，密度曲线越矮胖；当标准差相同时，均值越大，密度曲线越往右移。

5.2.2 指数分布

import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成各种指数分布随机数
np.random.seed(1234)
re1 = np.random.exponential(scale = 0.5, size = 1000)
re2 = np.random.exponential(scale = 1, size = 1000)
re3 = np.random.exponential(scale = 1.5, size = 1000)
# 绘图
sns.distplot(re1, hist = False, kde = False, fit = stats.expon, 
             fit_kws = {'color':'black','label':'lambda=0.5','linestyle':'-'})
sns.distplot(re2, hist = False, kde = False, fit = stats.expon, 
             fit_kws = {'color':'red','label':'lambda=1','linestyle':'--'})
sns.distplot(re3, hist = False, kde = False, fit = stats.expon, 
             fit_kws = {'color':'blue','label':'lambda=1.5','linestyle':':'})
# 呈现图例
plt.legend()
# 呈现图形
plt.show()

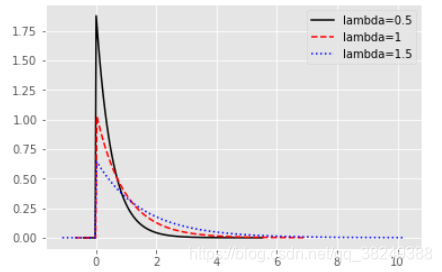
通过图形可知，指数分布的概率密度曲线呈现在y=0的右半边，而且随着lambda参数的增加，概率密度曲线表现得越矮，同时右边的“尾巴”会更长而厚。

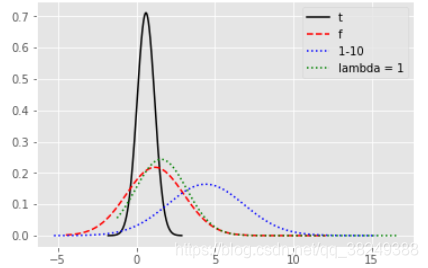
5.2.3 其它常用的分布

import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成随机数
np.random.seed(1234)
 
# 自由度为2的t分布
rn1 = np.random.standard_t(df = 3, size = (2,3))
 
# 自由度为2和5的f分布
rn2 = np.random.f(dfnum = 2,dfden = 5,size=(3,5)) 

# 1-10 之间的均匀分布，并四舍五入取整
rn3 = np.round(np.random.uniform(size=(3,4), low = 1, high = 10), 0)


# 绘图
plt.style.use('ggplot')
sns.distplot(rn1, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'black','label':'t ','linestyle':'-'})
sns.distplot(rn2, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'red','label':'f ','linestyle':'--'})
sns.distplot(rn3, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {'color':'blue','label':'1-10 ','linestyle':':'})

# 呈现图例
plt.legend()
# 呈现图形
plt.show()