【CS224n-2019学习笔记】Lecture 1: Introduction and Word Vectors

 附上斯坦福cs224n-2019链接：https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1194/

文章目录

• 1.课程简单介绍
• 1.1 本课程目标
• 1.2 今年的课程与以往的不同
• 1.3 作业计划
• 2.人类语言和词义
• 2.1 我们应该如何表示一个单词的词义(word meaning)
• 2.2 我们如何在计算机中得到一个可用的词义(word meaning)
• 2.2.1 常见的解决方案:例如，使用WordNet
• 2.2.1.1 WordNet含义
• 2.2.1.2 WordNet等这类资源存在的问题
• 2.2.2 使用离散符号表示词，比如one-hot表示
• 2.2.2.1 one-hot表示
• 2.2.2.2 使用离散符号表示词存在的问题
• 2.2.2.3 可以尝试的解决办法
• 2.2.3 使用词的上下文(context)来表示词
• 2.2.3.1 分布式语义(Distributional semantics)
• 2.2.3.2 词向量
• 2.2.3.3 Word meaning as a neural word vector –visualization
• 3.Word2vec介绍
• 3.1 Word2vec概述
• 3.1.1 简介
• 3.1.2 窗口和$P(w^{t+j}|w^t)$计算过程示例
• 3.2 目标函数(objective function)
• 3.2.1 目标函数推导
• 3.2.2 目标函数
• 3.3 如何训练模型
• 3.3.1 模型训练示例
• 3.3.2 模型训练：计算**所有**词向量的梯度
• 4.Word2vec目标函数梯度
• 4.1 补充知识
• 4.1.1 链式法则
• 4.1.2 向量求导
• 4.2 白板推导
• 4.3 计算梯度
• 4.4 关于Word2vec的细节
• 5.优化基础
• 5.1 梯度下降法介绍
• 5.1.1 示例
• 5.1.2 梯度更新
• 5.2 梯度下降法分类
• 6.词向量的简单演示

1.课程简单介绍

1.1 本课程目标

1. An understanding of the effective modern methods for deep learning

• Basics first, then key methods used in NLP: Recurrent networks, attention, etc.

2. A big picture understanding of human languages and the difficulties in understanding and producing them
3. An understanding of and ability to build systems (in PyTorch) for some of the major problems in NLP:

• Word meaning, dependency parsing, machine translation, question answering

1.2 今年的课程与以往的不同

1. Lectures (including guest lectures) covering new material: character models, transformers, safety/fairness, multitask learn.
2. 5x one-week assignments instead of 3x two-week assignments
3. Assignments covering new material (NMT with attention, ConvNets, subwordmodeling)
4. Using PyTorchrather than TensorFlow
5. Gentler but earlier ramp-up
6. First assignment is easy, but due one week from today!

1.3 作业计划

1. HW1 is hopefully an easy on ramp –an IPythonNotebook
2. HW2 is pure Python (numpy) but expects you to do (multivariate) calculus so you really understand the basics
3. HW3 introduces PyTorch
4. HW4 and HW5 use PyTorch on a GPU (Microsoft Azure)

• Libraries like PyTorch, Tensorflow(and Chainer, MXNet, CNTK, Keras, etc.) are becoming the standard tools of DL
  5.For FP, you either

• Do the default project, which is SQuAD question answering

   Open-ended but an easier start; a good choice for most
  

• Propose a custom final project, which we approve

  You will receive feedback from a mentor(TA/prof/postdoc/PhD) 
  

2.人类语言和词义

2.1 我们应该如何表示一个单词的词义(word meaning)

首先我们来看一下韦伯斯特词典对于meaning的定义：

• the idea that is represented by a word, phrase, etc.
• the idea that a person wants to express by using words, signs, etc.
• the idea that is expressed in a work of writing, art, etc.

然后看一下最常见的思考meaning的语言学方式：

denotational semantics是指称语义的意思，在视频中教授解释说，指称语义的想法是把meaning视为事物的代表(也就是signifier“能指”，一种符号),比如我们说到“椅子”，那么椅子这个词的meaning就指示了我们现实世界中的椅子这种物体(signified“所指”，想法或者事物)

我们现在知道了词义的概念，下一步就是想我们如何在计算机中得到一个可用的词义。

2.2 我们如何在计算机中得到一个可用的词义(word meaning)

2.2.1 常见的解决方案:例如，使用WordNet

2.2.1.1 WordNet含义

WordNet是一个包含同义词集列表和上义词(“is a”关系)的库。

2.2.1.2 WordNet等这类资源存在的问题

1. Great as a resource but missing nuance(细微差别)

• e.g. “proficient” is listed as a synonym for “good”. This is only correct in some contexts.

2. Missing new meanings of words

• e.g., wicked, badass, nifty, wizard, genius, ninja, bombest
• Impossible to keep up-to-date!

3. Subjective
4. Requires human labor to create and adapt
5. Can’t compute accurate word similarity

2.2.2 使用离散符号表示词，比如one-hot表示

2.2.2.1 one-hot表示

在传统的NLP中，我们视单词为离散的符号。one-hot的意思就是一个词向量中只有1个位置为1，剩下的位置全部为0，因此也可以翻译作独热。

词向量的维度 = 词表(不含重复词)中单词的数量(比如, 500,000)。

比如hotel,conference,motel的一个本地表示(localist representation)是：
motel = [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
hotel = [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]

2.2.2.2 使用离散符号表示词存在的问题

Example: in web search, if user searches for “Seattle motel”, we would like to match documents containing “Seattle hotel”.

但是我们上面也看到了motel和hotel的表示，可以发现：

• 这两个向量是正交的，也就是说点积为0;
• 因此，在one-hot向量中没有一个自然的相似的概念。也就是说使用one-hot向量很难度量词之间的相似度。

2.2.2.3 可以尝试的解决办法

1. 可以依靠WordNet的同义词集列表去得到相似度？

• 但众所周知，很失败:比如同义词集不完整等等，其实我觉得还是因为上面提到的WordNet存在的问题，比如很难及时更新等。

2. 试着在向量本身中去编码相似度。

2.2.3 使用词的上下文(context)来表示词

2.2.3.1 分布式语义(Distributional semantics)

1. 分布式语义:一个单词的词义是由频繁出现在它附近的词给出的(A word’s meaning is given by the words that frequently appear close-by);

对于分布式语义的评价：

• “You shall know a word by the company it keeps”(J. R. Firth 1957: 11)
• One of the most successful ideas of modern statistical NLP!

2. 当一个词w出现在一段文本中，它的上下文(context)就是这段文本中在它附近一个固定窗口(window)内出现的词的集合(When a word w appears in a text, its context is the set of words that appear nearby (within a fixed-size window).）
3. 基于以上理论，我们就可以使用w的多个上下文来建立w的表示。比如：
   

2.2.3.2 词向量

我们为每个单词构建一个稠密的向量，使其与出现在类似上下文中的单词的向量相似。

Note:

• 词向量有时也称作是词嵌入 或者 词表示。他们都是一种分布式表示。
• one-hot表示，有时也称作离散/稀疏 表示；
• 分布式表示(distributed representation)，称作稠密 表示(dense representation)

2.2.3.3 Word meaning as a neural word vector –visualization

3.Word2vec介绍

3.1 Word2vec概述

3.1.1 简介

Word2vec (Mikolovet al. 2013)是一个学习词语向量表示(词向量)的框架。

Word2vec的主要想法(Idea):

• 我们有一个大型的的文本语料库
• 在一个固定词汇表中的每个单词都由一个向量表示(is represented by a vector)
• 遍历文本中的每个位置t，其中有一个中心词(center word)c和上下文(outside,“外部”)单词o
• 使用单词向量c和o的相似度来计算P(o|c),反之亦然
• 不断调整单词向量来最大化这个概率

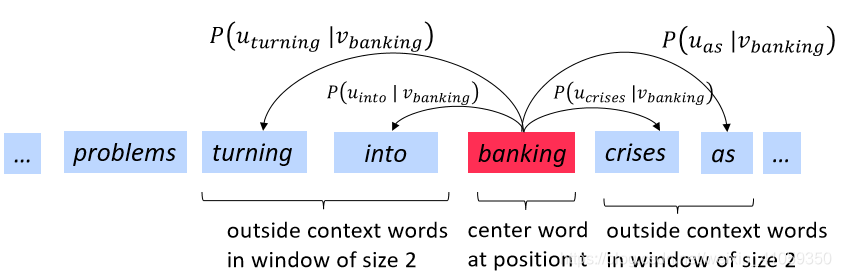
3.1.2 窗口和$P(w^{t+j}|w^t)$计算过程示例

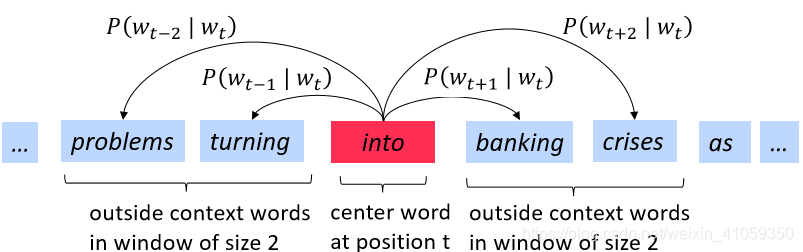
3.2 目标函数(objective function)

3.2.1 目标函数推导

对于每个位置t=1,…,T，给定一个中心词$w^t$,预测一个固定大小的窗口(大小为m)内的上下文单词：
$$Likelyhood=L(\theta )=\stackrel{T\prod }{t=1}\stackrel{\prod }{-m⩽j⩽m，j�=0}P(w^{t+j}|w^t;\theta )$$

• 最大化上面这个函数就可以达到我们的目的，即最大化预测精度
• $\theta$代表所有待优化的变量

但是上面这种形式(连乘)不适合求导，因此需要做一定的转换，log转换可以把连乘变成累加，并且不改变原函数的单调性。于是最终的目标函数为：
$$J(\theta )=-\genfrac{}{}{0ex}{}{1}{T}logL(\theta )=-\genfrac{}{}{0ex}{}{1}{T}\stackrel{T\sum }{t=1}\stackrel{\sum }{-m⩽j⩽m，j�=0}logP(w^{t+j}|w^t;\theta )$$

• 这样最大化预测精度的问题就转变成了最小化目标函数的问题，即最小化目标函数等价于最大化预测精度

3.2.2 目标函数

• 现在我们要最小化目标函数J(θ)：
  $$J(\theta )=-\genfrac{}{}{0ex}{}{1}{T}\stackrel{T\sum }{t=1}\stackrel{\sum }{-m⩽j⩽m，j�=0}logP(w^{t+j}|w^t;\theta )$$
• 还有一个问题，我们如何计算$P(w^{t+j}|w^t;\theta )$。因为在遍历过程中，每个单词有时是中心词，有时是上下文。
• 解决方案：对每个单词w使用两个向量表示：
  • 当w是中心词的时候，用向量$v^w$表示
  • 当w是上下文词的时候，用向量$u^w$表示
• 然后对于一个中心词c和一个上下文词o，计算公式：
  $$P(o|c)=\genfrac{}{}{0ex}{}{exp(u^o{v}^c)}{{\sum }^{w\in V}exp(u^w{v}^c)}$$
• 向量示例如下：
  
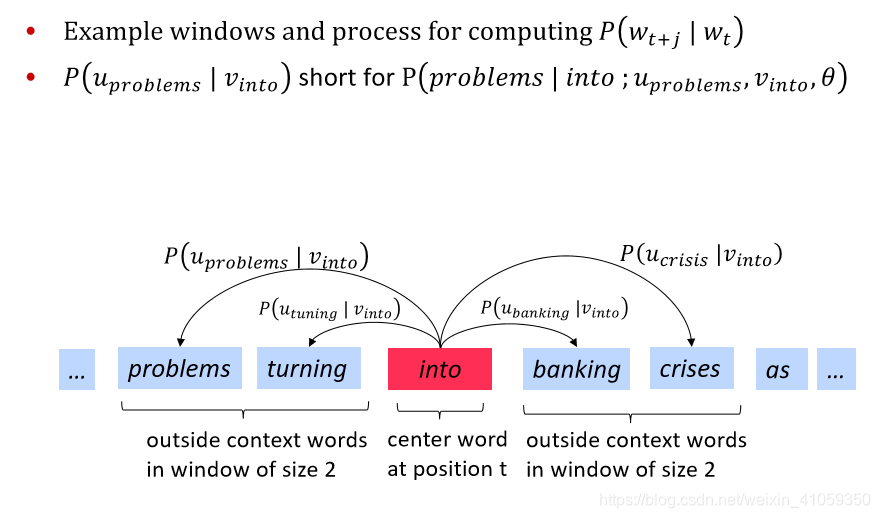
  Note:
• 上述计算公式是softmax函数，一般形式是：
  $$softmax(x^i)=\genfrac{}{}{0ex}{}{exp(x^i)}{{\sum }^{j=1}exp(x^j)}$$
• softmax函数将任意值$x^i$映射到一个概率分布$p^i$
  • “max”:是因为会放大较大的$x^i$的概率
  • “soft”:是因为也会给较小的$x^i$赋一些概率值
  • softmax函数经常用在深度学习中

3.3 如何训练模型

3.3.1 模型训练示例

通常训练一个模型的时候，我们需要调整参数，最小化损失函数。

• 例子：下面是对于一个简单凸函数的两个参数的优化，等高线表示目标函数的值
  

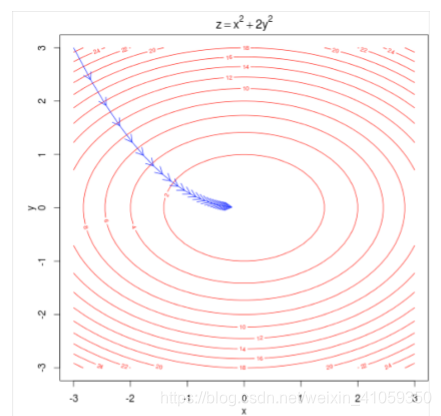
3.3.2 模型训练：计算所有词向量的梯度

• 前面说了，θ是一个长向量，代表了模型中的所有参数
• 在这里，词向量是d维，共有V个词：
  
  • 注意，每个词有两个向量，分别是作为中心词、上下文词时的向量
  • 沿着梯度的反方向，优化以上参数

4.Word2vec目标函数梯度

4.1 补充知识

4.1.1 链式法则

用于复合函数求导，有$y=f(u),u=g(x)$，则：
$$\genfrac{}{}{0ex}{}{dy}{dx}=\genfrac{}{}{0ex}{}{dy}{du}\genfrac{}{}{0ex}{}{du}{dx}$$

4.1.2 向量求导

$$\genfrac{}{}{0ex}{}{\partial x^{T}a}{\partial x}=\genfrac{}{}{0ex}{}{\partial a^{T}x}{\partial x}=a$$

• 其中，x、a默认为列向量
• 上式求导为标量对向量求导，分子布局：n维行向量，分母布局：n维列向量（默认布局）${}^{[2]}$（关于具体的推导步骤：见评论区链接）

4.2 白板推导

有了上述补充知识之后，就开始进行求偏导数的白板推导，视频中教授只对一个中心词进行了求导演示，以下是我跟着视频推导的过程(感兴趣的可以看看这部分视频，讲解非常清晰)：

• 上面演示了损失函数对一个中心词的求导，另外还需要推导损失函数对于上下文词的求导，感兴趣的可以自己试一下。最终推出对θ中每个向量元素的偏导数。
• 我的推导如下：
  

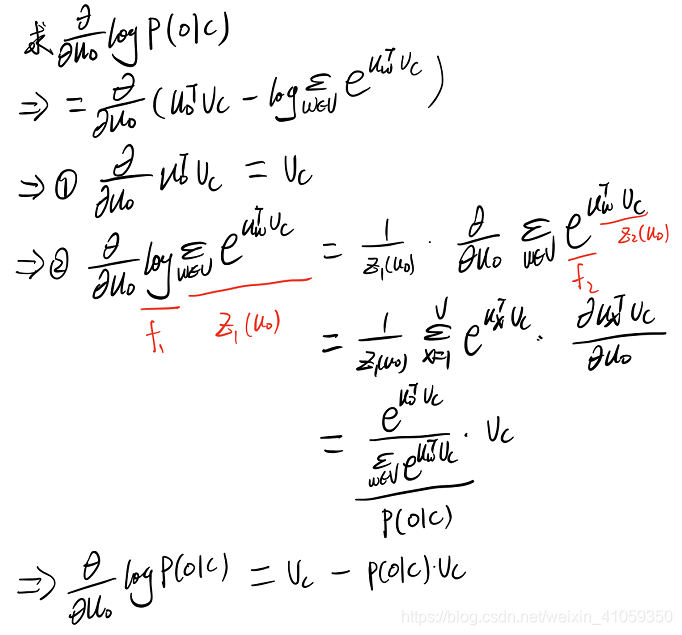
4.3 计算梯度

• 遍历每一个在一个固定窗口内的中心词的梯度
• 同样也需要上下文词的梯度
• 通常，在每个窗口内，我们会更新这个窗口内用到的所有参数，比如：
  

4.4 关于Word2vec的细节

为什么同一个词需要两个向量？

• 更易进行优化
• 在训练完成后将两者取平均，即为该词的词向量

有两种模型：

• Skip-gram(SG):通过中心词预测上下文词
• Continuous Bag of Words(CBOW):使用窗口内的所有上下文词预测中心词
• 本文上面讲述的是Skip-gram模型

其他令训练更有效的手段：

• 负采样(negative sampling)
• 本文上面讲的是很简单的训练方法

5.优化基础

5.1 梯度下降法介绍

5.1.1 示例

• 假设我们有一个损失函数$J(\theta )$，要最小化
• 梯度下降法就是一种可以最小化$J(\theta )$的算法
• 主要想法：
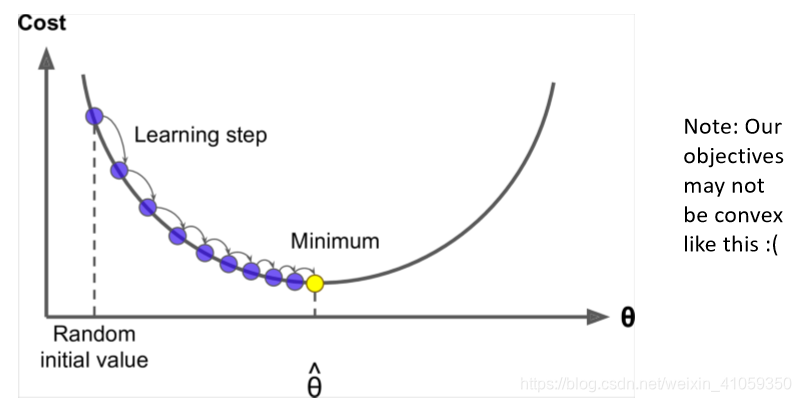
  • 对于当前的θ值，计算J(θ)对于θ的梯度，然后将θ沿着梯度的反方向走一小步。重复此步骤，直至满足停止条件。
    

5.1.2 梯度更新

• 矩阵形式更新：
  $${\theta }^{new}={\theta }^{old}-\alpha \nabla \theta J(\theta )$$
• 单个参数更新，要注意参数必须同时更新：
  $${\theta }^j={\theta }^j-\alpha \genfrac{}{}{0ex}{}{\partial }{\partial {\theta }^j}J(\theta )$$
• α称为学习率(learning rate)

5.2 梯度下降法分类

根据每次迭代时使用的样本量大致分为：

• 批量梯度下降法(Batch GD，BGD)：每次迭代使用全部的样本对参数进行更新
• 随机梯度下降法(Stochastic，SGD)：每次迭代使用一个样本对参数进行更新
• 小批量梯度下降法(Mini-Batch GD，MBGD)：每次迭代使用batch_size个样本对参数进行更新

更加详细的介绍见批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解

6.词向量的简单演示

教授利用Glove词向量做了一些简单展示：

• 相似词：找和某个词向量最相似的那个词，model.most_similar(“banana”)
• 词类比：比如king之于man，等于queen之于woman，也是词在向量空间king-man+woman=queen
• 可视化：将词向量利用PCA降到二维，并进行可视化，可以发现相似概念的词距离很接近，最终结果如下所示：
  

---

参考资料：
1.2019斯坦福公开课CS224N-P1
2.矩阵向量求导-求导定义与求导布局