机器学习-牛顿方法&指数分布族&GLM

本节内容

• 牛顿方法
• 指数分布族
• 广义线性模型

之前学习了梯度下降方法，关于梯度下降（gradient descent），这里简单的回顾下【参考感知机学习部分提到的梯度下降(gradient descent)】。在最小化损失函数时，采用的就是梯度下降的方法逐步逼近最优解，规则为其实梯度下降属于一种优化方法，但梯度下降找到的是局部最优解。如下图：

本节首先讲解的是牛顿方法（NewTon’s Method）。牛顿方法也是一种优化方法，它考虑的是全局最优。接着还会讲到指数分布族和广义线性模型。下面来详细介绍。

1.牛顿方法

现在介绍另一种最小化损失函数ℓ(θ)的方法——牛顿方法,参考Approximations Of Roots Of Functions – Newton’s Method
。它与梯度下降不同，其基本思想如下：

假设一个函数我们需要求解此时的x值。如下图所示：

图1 f(x0)=0,a1,a2,a3...逐步接近x0

在a1点的时候，f(x)切线的目标函数由于(a2,0)在这条线上，所以我们有

同理，在a2点的时候，切线的目标函数由于(a3,0)在这条线上，所以我们有

假设在第n次迭代，有那么此时有下面这个递推公式：

其中n>=2。

最后得到的公式也就是牛顿方法的学习规则，为了和梯度下降对比，我们来替换一下变量，公式如下：

那么问题来了，怎么将牛顿方法应用到我们的问题上，最小化损失函数l(theta),(或者是求极大似然估计的极大值)呢？

对于机器学习问题，现在我们优化的目标函数为极大似然估计l,当极大似然估计函数取值最大时，其导数为 0，这样就和上面函数f取 0 的问题一致了，令极大似然函数的求解更新规则是：

对于l,当一阶导数为零时，有极值；此时，如果二阶导数大于零，则l有极小值，如果二阶导数小于零，则有极大值。

上面的式子是当参数θ为实数时的情况，下面我们要求出一般式。当参数为向量时，更新规则变为如下公式：

其中和之前梯度下降中提到的一样，是梯度，H是一个n*n矩阵，H是函数的二次导数矩阵，被成为Hessian矩阵。其某个元素H_ij计算公式如下：

和梯度下降相比，牛顿方法的收敛速度更快，通常只要十几次或者更少就可以收敛，牛顿方法也被称为二次收敛（quadratic convergence），因为当迭代到距离收敛值比较近的时候，每次迭代都能使误差变为原来的平方。缺点是当参数向量较大的时候，每次迭代都需要计算一次 Hessian 矩阵的逆，比较耗时。

2.指数分布族（The exponential family）

指数分布族是指可以表示为指数形式的概率分布。指数分布的形式如下：

其中，η成为分布的自然参数（nature parameter）；T(y)是充分统计量（sufficient statistic），通常 T(y)=y。当参数 a、b、T 都固定的时候，就定义了一个以η为参数的函数族。

下面介绍两种分布，伯努利分布和高斯分布，分别把它们表示成指数分布族的形式。

伯努利分布

伯努利分布是对0，1问题进行建模的，对于有下面将其推导成指数分布族形式：

将其与指数族分布形式对比，可以看出：

表明伯努利分布也是指数分布族的一种。从上述式子可以看到，η的形式与logistic函数（sigmoid）一致，这是因为 logistic模型对问题的前置概率估计其实就是伯努利分布。

高斯分布

下面对高斯分布进行推导，推导公式如下（为了方便计算，我们将方差σ设置为1）：

将上式与指数族分布形式比对，可知：

两个典型的指数分布族，伯努利和高斯分布。其实大多数概率分布都可以表示成指数分布族形式，如下所示：

• 伯努利分布（Bernoulli）：对 0、1 问题进行建模；
• 多项式分布（Multinomial）：多有 K 个离散结果的事件建模；
• 泊松分布（Poisson）：对计数过程进行建模，比如网站访问量的计数问题，放射性衰变的数目，商店顾客数量等问题；
• 伽马分布（gamma）与指数分布（exponential）：对有间隔的正数进行建模，比如公交车的到站时间问题；
• β 分布：对小数建模；
• Dirichlet 分布：对概率分布进建模；
• Wishart 分布：协方差矩阵的分布；
• 高斯分布（Gaussian）；

下面来介绍下广义线性模型（Generalized Linear Model, GLM）。

3.广义线性模型（Generalized Linear Model, GLM）

你可能会问，指数分布族究竟有何用？其实我们的目的是要引出GLM，通过指数分布族引出广义线性模型。

仔细观察伯努利分布和高斯分布的指数分布族形式中的η变量。可以发现，在伯努利的指数分布族形式中，η与伯努利分布的参数φ是一个logistic函数（下面会介绍logistic回归的推导）。此外，在高斯分布的指数分布族表示形式中，η与正态分布的参数μ相等，下面会根据它推导出普通最小二乘法（Ordinary Least Squares）。通过这两个例子，我们大致可以得到一个结论，η以不同的映射函数与其它概率分布函数中的参数发生联系，从而得到不同的模型，广义线性模型正是将指数分布族中的所有成员（每个成员正好有一个这样的联系）都作为线性模型的扩展，通过各种非线性的连接函数将线性函数映射到其他空间，从而大大扩大了线性模型可解决的问题。

下面我们看 GLM 的形式化定义，GLM 有三个假设：

• （1）；给定样本Χ与参数θ，样本分类γ服从指数分布族中的某个分布；
• （2）给定一个Χ，我们需要的目标函数为
• （3）。 

 依据这三个假设，我们可以推导出logistic模型与普通最小二乘模型。首先根据伯努利分布推导Logistic模型，推导过程如下:

公式第一行来自假设(2)，公式第二行通过伯努利分布计算得出，第三行通过伯努利的指数分布族表示形式得出，然后在公式第四行，根据假设三替换变量得到。

同样，可以根据高斯分布推导出普通最小二乘，如下：

公式第一行来自假设（2），第二行是通过高斯分布计算得出，第三行是通过高斯分布的指数分布族形式表示得出，第四行即为假设（3）。

其中，将η与原始概率分布中的参数联系起来的函数成为正则相应函数（canonical response function），如即是正则响应函数。正则响应函数的逆成为正则关联函数（canonical link function）。

所以，对于广义线性模型，需要决策的是选用什么样的分布，当选取高斯分布时，我们就得到最小二乘模型，当选取伯努利分布时，我们得到 logistic 模型，这里所说的模型是假设函数 h 的形式。

最后总结一下：广义线性模型通过假设一个概率分布，得到不同的模型，而梯度下降和牛顿方法都是为了求取模型中的线性部分的参数θ的。

多分类模型-Softmax Regression

下面再给出GLM的一个例子——Softmax Regression.

假设一个分类问题，y可取k个值，即y∈{1,2,...k}。现在考虑的不再是一个二分类问题，现在的类别可以是多个。如邮件分类：垃圾邮件、个人邮件、工作相关邮件。下面要介绍的是多项式分布（multinomial distribution）。

多项式分布推导出的GLM可以解决多类分类问题，是 logistic 模型的扩展。对于多项式分布中的各个y的取值，我们可以使用k个参数φ1,φ2,...,φk来表示这k个取值的概率。即

但是，这些参数可能会冗余，更正式的说可能不独立，因为，知道了前k-1个，就可以通过计算出第k个概率。所以，我们只假定前k-1个结果的概率参数φ1,φ2,...,φk-1，第k个输出的概率通过下面的式子计算得出：

为了使多项式分布能够写成指数分布族的形式，我们首先定义 T(y)，如下所示：

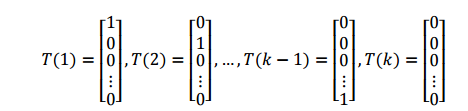
和之前的不一样，这里我们的T(y)不等γ，T(y)现在是一个k-1维的向量，而不是一个真实值。接下来，我们将使用表示T(y)的第i个元素。

下面我们引入指数函数I，使得：

这样，T(y)向量中的某个元素还可以表示成：

举例来说，当y=2时，。根据公式 15，我们还可以得到：

下面，二项分布转变为指数分布族的推导如下：

其中，最后一步的各个变量如下：

由η的表达式可知：

为了方便，再定义：

于是，可以得到：

将上式代入到，得到：

从而，我们就得到了连接函数，有了连接函数后，就可以把多项式分布的概率表达出来:

注意到，上式中的每个参数η_i都是一个可用线性向量表示出来的，因而这里的θ其实是一个二维矩阵。

于是，我们可以得到假设函数 h 如下：

那么就建立了假设函数，最后就获得了最大似然估计

对该式子可以使用梯度下降算法或者牛顿方法求得参数θ后，使用假设函数h对新的样例进行预测，即可完成多类分类任务。这种多种分类问题的解法被称为 softmax regression。

ηk=log

hθ(x

hθ(x)=