HDU3191 How Many Paths Are There

~~~~~~HDU3191 How Many Paths Are There ~~~~~~

大致题意：

给出一个有向图，求其次短路径数。

思路：

1. 首先，用一个邻接矩阵储存图，
   
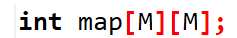
   再用几个数组记录标程
2. [0]表示最短路，[1]表示次短路。初始化图为-1，输入图，完成图的构建
3. 

在进行 dijkstra 的过程中记录两个数组：dist0 和 dist1，分别表示最短路和次短路的答案。每次更新时需要依次判断是否可以更新次短路和最短路的值。由于需要计算次短路，所以调整后的 dijkstra 算法需要至少循环 2n 次才可以获得最终答案。

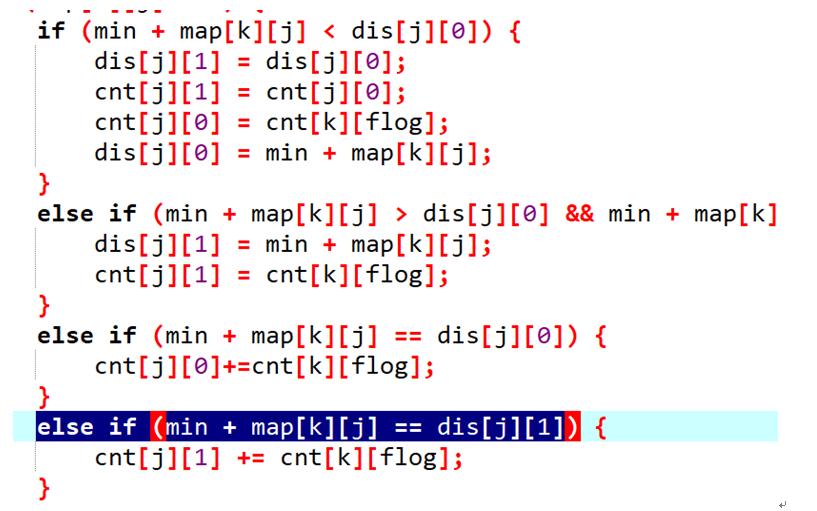
4.if (min + map[k][j] < dis[j][0]) 表示可以更新最短，那么同时次短也会被原来的最短所更新掉，产生了两个新状态，都要添加到队列中。

else if (min + map[k][j] == dis[j][0]) 表示最短路径增多了。

else if (min + map[k][j] > dis[j][0] && min + map[k][j] < dis[j][1])表示可以更新次短路，状态有改变，需要将新状态添加到队列中。

else if (min + map[k][j] == dis[j][1])表示次短路径增多了。

#include<iostream>
#include<string.h>
using namespace std;
#define M 51
#define inf 0x3f3f3f3f
int map[M][M];
int dis[M][2];
int vis[M][2];
int cnt[M][2];
int n, m, s, e;
void dij() {
    for(int i=0;i<n;i++){
        cnt[i][0]=0;
        cnt[i][1]=0;
        vis[i][0]=0;
        vis[i][1]=0;
    }
    //cout<<cnt[2][0]<<cnt[2][1];
//    vis[s][0]= 1;
//    
    for (int i = 0; i < n; i++) {
        //dis[i][0] = map[s][i];
        dis[i][0]=inf;
        dis[i][1] = inf;
    }
    dis[s][0]=0;
    cnt[s][0]=1;
    int min = inf;
    int k;
    int flog;
    for (int i = 0; i < n*2; i++) {
        min = inf;
        for (int j = 0; j < n; j++) {
            if (dis[j][0] < min && !vis[j][0]) {
                k = j;
                flog=0;
                min = dis[j][0];
            }else if(!vis[j][1]&&dis[j][1]<min){
                k=j;
                flog=1;
                min=dis[i][1];
            }

        }//cout << 1;
        if(min==inf) break; 
        vis[k][flog] = 1;
        for (int j = 0; j < n; j++) {
            //if (!vis[j]&&map[k][j]<inf) {
            if (map[k][j]!=-1) {
                if (min + map[k][j] < dis[j][0]) {
                    dis[j][1] = dis[j][0];
                    cnt[j][1] = cnt[j][0];
                    cnt[j][0] = cnt[k][flog];
                    dis[j][0] = min + map[k][j];
                }
                else if (min + map[k][j] > dis[j][0] && min + map[k][j] < dis[j][1]) {
                    dis[j][1] = min + map[k][j];
                    cnt[j][1] = cnt[k][flog];
                }
                else if (min + map[k][j] == dis[j][0]) {
                    cnt[j][0]+=cnt[k][flog];
                }
                else if (min + map[k][j] == dis[j][1]) {
                    cnt[j][1] += cnt[k][flog];
                }


            }

        }
    }
    cout << dis[e][1] << " " << cnt[e][1];
}
int main() {

    while (~scanf("%d%d%d%d", &n, &m, &s, &e)) {
        int x, y, z;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                map[i][j] = -1;
            }
        }
        for (int i = 0; i < m; i++) {
            scanf("%d%d%d", &x, &y, &z);
            map[x][y] = z;

        }

        dij();

    }
    return 0;
}