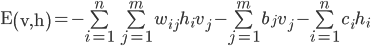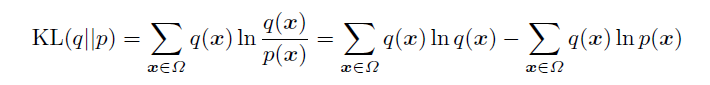受限玻尔兹曼机二

博主falao_beiliu写的一篇非常好的文章。
这里为方便自己以后速查，做个导航。

---

原文目录：

1. 限制波尔兹曼机RBM使用方法
2. 限制波尔兹曼机RBM能量模型
3. 从能量模型到概率
4. 求解极大似然
5. 用到的抽样方法
6. 马尔科夫蒙特卡罗简介
7. 参考文献

原文链接：

https://blog.csdn.net/mytestmy/article/details/9150213

---

阅读原文之后的一些简单概括：
(1) 每一层的每一个unit是如何激活的？

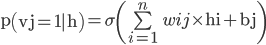
利用上面的公式得到的是某个单元状态为1的输出概率。那么怎样才能确定这个单元的状态是1呢？
它通过产生一个0~1的随机，如果这个随机数小于上面得到的概率值，这个单元的状态就确定为1，反之这认为这个单元的状态为0.举个栗子，P(h_i=1|v) = 0.7， 随机数为0.5， 0.7>0.5，我们就认为这个单元的状态为1.

(2) 能量模型
三个概念: 状态，能量，概率
一个物体处在一个什么的状态，如在RBM里就是一个单元是0还是1；
处于某一个状态的能量，用E表示；
处在这个状态下的概率是多少,用P表示，P=f(E)$P=f(E)$,其中f$f$是能量函数。
P=f(E)$P=f(E)$就是能量模型。

(3) 能量函数的理解
能量函数的定义如下

“每个可视节点和隐藏节点之间的连接结构都有一个能量，通俗来说就是可视节点的每一组取值和隐藏节点的每一组取值都有一个能量，如果可视节点的一组取值（也就是一个训练样本的值）为(1,0,1,0,1,0)，隐藏节点的一组取值（也就是这个训练样本编码后的值）为(1,0,1)，然后分别代入上面的公式，就能得到这个连接结构之间的能量”。

(4)可视节点和隐藏节点的联合分布
在统计热力学中，当系统与外界处于热平衡时，一个状态i发生的概率为

Pi=1Z×e−Eikb×T$$P_i=\frac{1}{Z}\times e^{\frac{-E_i}{kb\times T}}$$

定义可视节点和隐藏节点的联合概率

p(v,h)=e−E(v,h)∑v,he−E(v,h)$$p(v,h)=\frac{e^{-E(v,h)}}{\sum _{v,h}{e}^{-E(v,h)}}$$

从联合概率密度可以得到其他的概率：

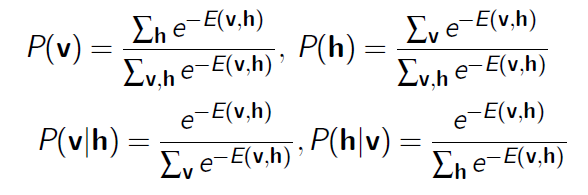
(5) RBM干了些什么事情？
上面定义能量函数和一个联合概率。换句话说，我们已经把每一种输入与一个概率想对应了。然而这个概率并不是数据原本的概率分布，而是我们想象的，能够最大可能拟合输入数据的概率分布。

(6) kl距离
引用作者的原话：

假设Ω表示样本空间，q是输入样本的分布，即q(x)表示训练样本x的概率，
q是要拟合的那个样本表示分布的概率；
假设p是RBM网络表示的Gibbs分布的边缘分布（只跟可视节点有关，隐藏节点是通过积分去掉了，可以理解为可视节点的各个状态的分布）；
输入样本的集合是S，那现在就可以定义样本表示的分布和RBM网络表示的边缘分布的KL距离

KL距离描述了两个分布的相似程度，KL距离大于零。KL距离越小，两个分布越相似。
上式中第一项是熵，由输入决定；第二项无法直接求解。

(7) 通过极大似然估计求解参数