---------------------siwuxie095
Dijkstra 算法
这里介绍 Dijkstra 算法,它是一个应用最为广泛的、名气也是
最大的单源最短路径算法
Dijkstra 算法有一定的局限性:它所处理的图中不能有负权边
「前提:图中不能有负权边」
换句话说,如果一张图中,但凡有一条边的权值是负值,那么
使用 Dijkstra 算法就可能得到错误的结果
不过,在实际生活中所解决的问题,大部分的图是不存在负权
边的
如:有一个路线图,那么从一点到另外一点的距离肯定是一个
正数
所以,虽然 Dijkstra 算法有局限性,但是并不影响在实际问题
的解决中非常普遍的来使用它
看如下实例:
(1)初始

左边是一张连通带权有向图,右边是起始顶点 0 到各个顶点的
当前最短距离的列表,起始顶点 0 到自身的距离是 0
(2)将顶点 0 进行标识,并作为当前顶点

对当前顶点 0 的所有相邻顶点依次进行松弛操作,同时更新列表
从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 2,
就可以说,起始顶点 0 到顶点 2 的最短路径即 0 -> 2
因为:图中没有负权边,即便存在从顶点 1 到顶点 2 的边,也不
可能通过松弛操作使得从起始顶点 0 到顶点 2 的距离更小
图中没有负权边保证了:对当前顶点的所有相邻顶点依次进行松
弛操作后,只要能从列表的未标识顶点中找到当前最短距离最小
的顶点,就能确定起始顶点到该顶点的最短路径
(3)将顶点 2 进行标识,并作为当前顶点

(4)对当前顶点 2 的相邻顶点 1 进行松弛操作,同时更新列表

(5)对当前顶点 2 的相邻顶点 4 进行松弛操作,同时更新列表

(6)对当前顶点 2 的相邻顶点 3 进行松弛操作,同时更新列表

从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 1,
就可以说,起始顶点 0 到顶点 1 的最短路径即 0 -> 2 -> 1
(7)将顶点 1 进行标识,并作为当前顶点

(8)对当前顶点 1 的相邻顶点 4 进行松弛操作,同时更新列表

从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 4,
就可以说,起始顶点 0 到顶点 4 的最短路径即 0 -> 2 -> 1 -> 4
(9)将顶点 4 进行标识,并作为当前顶点

当前顶点 4 没有相邻顶点,不必进行松弛操作
从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 3,
就可以说,起始顶点 0 到顶点 3 的最短路径即 0 -> 2 -> 3
(10)将顶点 3 进行标识,并作为当前顶点

对当前顶点 3 的相邻顶点 4 进行松弛操作,发现不能通过
松弛操作使得从起始顶点 0 到顶点 4 的路径更短,所以保
持原有最短路径不变
至此,列表中不存在未标识顶点,Dijkstra 算法结束,找
到了一棵以顶点 0 为根的最短路径树
Dijkstra 算法的过程总结:
第一步:从起始顶点开始
第二步:对当前顶点进行标识
第三步:对当前顶点的所有相邻顶点依次进行松弛操作
第四步:更新列表
第五步:从列表的未标识顶点中找到当前最短距离最小
的顶点,作为新的当前顶点
第六步:重复第二步至第五步,直到列表中不存在未标
识顶点
其实 Dijkstra 算法主要做两件事情:
(1)从列表中找最值
(2)更新列表
显然,借助最小索引堆作为辅助数据结构,就可以非常
容易地实现这两件事情
最后,Dijkstra 算法的时间复杂度:O(E*logV)
程序:
Edge.h:
|
#ifndef EDGE_H #define EDGE_H
#include <iostream> #include <cassert> using namespace std;
//边信息:两个顶点和权值 template<typename Weight> class Edge {
private:
int a, b; //边的两个顶点a和b(如果是有向图,就默认从顶点a指向顶点b) Weight weight; //边上的权值
public:
Edge(int a, int b, Weight weight) { this->a = a; this->b = b; this->weight = weight; }
//默认构造函数 Edge(){}
~Edge(){}
int v(){ return a; }
int w(){ return b; }
Weight wt() { return weight; }
//知道边的一个顶点x,返回另一个顶点 int other(int x) { assert(x == a || x == b); return x == a ? b : a; }
//友元函数重载 friend ostream &operator<<(ostream &os, const Edge &e) { os << e.a << "-" << e.b << ": " << e.weight; return os; }
bool operator<(Edge<Weight> &e) { return weight < e.wt(); }
bool operator<=(Edge<Weight> &e) { return weight <= e.wt(); }
bool operator>(Edge<Weight> &e) { return weight > e.wt(); }
bool operator>=(Edge<Weight> &e) { return weight >= e.wt(); }
bool operator==(Edge<Weight> &e) { return weight == e.wt(); } };
#endif |
SparseGraph.h:
|
#ifndef SPARSEGRAPH_H #define SPARSEGRAPH_H
#include "Edge.h" #include <iostream> #include <vector> #include <cassert> using namespace std;
// 稀疏图 - 邻接表 template<typename Weight> class SparseGraph {
private:
int n, m; //n 和 m 分别表示顶点数和边数 bool directed; //directed表示是有向图还是无向图 vector<vector<Edge<Weight> *>> g; //g[i]里存储的就是和顶点i相邻的所有边指针
public:
SparseGraph(int n, bool directed) { this->n = n; this->m = 0; this->directed = directed; //g[i]初始化为空的vector for (int i = 0; i < n; i++) { g.push_back(vector<Edge<Weight> *>()); } }
~SparseGraph() {
for (int i = 0; i < n; i++) { for (int j = 0; j < g[i].size(); j++) { delete g[i][j]; } } }
int V(){ return n; } int E(){ return m; }
void addEdge(int v, int w, Weight weight) { assert(v >= 0 && v < n); assert(w >= 0 && w < n);
g[v].push_back(new Edge<Weight>(v, w, weight)); //(1)顶点v不等于顶点w,即不是自环边 //(2)且不是有向图,即是无向图 if (v != w && !directed) { g[w].push_back(new Edge<Weight>(w, v, weight)); }
m++; }
//hasEdge()判断顶点v和顶点w之间是否有边 //hasEdge()的时间复杂度:O(n) bool hasEdge(int v, int w) { assert(v >= 0 && v < n); assert(w >= 0 && w < n);
for (int i = 0; i < g[v].size(); i++) { if (g[v][i]->other(v) == w) { return true; } }
return false; }
void show() {
for (int i = 0; i < n; i++) { cout << "vertex " << i << ": "; for (int j = 0; j < g[i].size(); j++) { cout << "{to:" << g[i][j]->w() << ",wt:" << g[i][j]->wt() << "} "; } cout << endl; } }
//邻边迭代器(相邻,即 adjacent) // //使用迭代器可以隐藏迭代的过程,按照一定的 //顺序访问一个容器中的所有元素 class adjIterator { private:
SparseGraph &G; //图的引用,即要迭代的图 int v; //顶点v int index; //相邻顶点的索引
public:
adjIterator(SparseGraph &graph, int v) : G(graph) { this->v = v; this->index = 0; }
//要迭代的第一个元素 Edge<Weight> *begin() { //因为有可能多次调用begin(), //所以显式的将index设置为0 index = 0; //如果g[v]的size()不为0 if (G.g[v].size()) { return G.g[v][index]; }
return NULL; }
//要迭代的下一个元素 Edge<Weight> *next() { index++; if (index < G.g[v].size()) { return G.g[v][index]; }
return NULL; }
//判断迭代是否终止 bool end() { return index >= G.g[v].size(); } }; };
#endif |
DenseGraph.h:
|
#ifndef DENSEGRAPH_H #define DENSEGRAPH_H
#include "Edge.h" #include <iostream> #include <vector> #include <cassert> using namespace std;
// 稠密图 - 邻接矩阵 template<typename Weight> class DenseGraph {
private:
int n, m; //n 和 m 分别表示顶点数和边数 bool directed; //directed表示是有向图还是无向图 vector<vector<Edge<Weight> *>> g; //二维矩阵,存储边指针
public:
DenseGraph(int n, bool directed) { this->n = n; this->m = 0; this->directed = directed; //二维矩阵:n行n列,全部初始化为NULL for (int i = 0; i < n; i++) { g.push_back(vector<Edge<Weight> *>(n, NULL)); } }
~DenseGraph() { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (g[i][j] != NULL) { delete g[i][j]; } } } }
int V(){ return n; } int E(){ return m; }
//在顶点v和顶点w之间建立一条边 void addEdge(int v, int w, Weight weight) { assert(v >= 0 && v < n); assert(w >= 0 && w < n);
//如果顶点v和顶点w之间已经存在一条边,就删掉, //之后按照传入权值重建一条边,即直接覆盖 if (hasEdge(v, w)) { delete g[v][w];
//如果是无向图,还要删除和主对角线对称的值 if (!directed) { delete g[w][v]; }
m--; }
g[v][w] = new Edge<Weight>(v, w, weight);
//如果是无向图,还要在和主对角线对称处添加值 if (!directed) { g[w][v] = new Edge<Weight>(w, v, weight); }
m++; }
//hasEdge()判断顶点v和顶点w之间是否有边 //hasEdge()的时间复杂度:O(1) bool hasEdge(int v, int w) { assert(v >= 0 && v < n); assert(w >= 0 && w < n); return g[v][w] != NULL; }
void show() {
for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (g[i][j]) { cout << g[i][j]->wt() << " "; } else { cout << "NULL "; } } cout << endl; } }
//邻边迭代器(相邻,即 adjacent) class adjIterator { private:
DenseGraph &G; //图引用,即要迭代的图 int v; //顶点v int index; //相邻顶点的索引
public:
adjIterator(DenseGraph &graph, int v) : G(graph) { this->v = v; this->index = -1; }
//要迭代的第一个元素 Edge<Weight> *begin() { //找第一个权值不为NULL的元素,即为要迭代的第一个元素 index = -1; return next(); }
//要迭代的下一个元素 Edge<Weight> *next() { for (index += 1; index < G.V(); index++) { if (G.g[v][index]) { return index; } }
return NULL; }
//判断迭代是否终止 bool end() { return index >= G.V(); } }; };
#endif |
ReadGraph.h:
|
#ifndef READGRAPH_H #define READGRAPH_H
#include <iostream> #include <string> #include <fstream> #include <sstream> #include <cassert> using namespace std;
//从文件中读取图的测试用例 template <typename Graph, typename Weight> class ReadGraph {
public: ReadGraph(Graph &graph, const string &filename) {
ifstream file(filename); string line; //一行一行的读取 int V, E;
assert(file.is_open());
//读取file中的第一行到line中 assert(getline(file, line)); //将字符串line放在stringstream中 stringstream ss(line); //通过stringstream解析出整型变量:顶点数和边数 ss >> V >> E;
//确保文件里的顶点数和图的构造函数中传入的顶点数一致 assert(V == graph.V());
//读取file中的其它行 for (int i = 0; i < E; i++) {
assert(getline(file, line)); stringstream ss(line);
int a, b; Weight w; ss >> a >> b >> w; assert(a >= 0 && a < V); assert(b >= 0 && b < V); graph.addEdge(a, b, w); } } };
#endif |
MinIndexHeap.h:
|
#ifndef MININDEXHEAP_H #define MININDEXHEAP_H
#include <iostream> #include <string> #include <cassert> #include <algorithm> using namespace std;
//最小索引堆:索引从0开始 template<typename Item> class MinIndexHeap {
private: Item *data; //指向存储元素的数组 int *indexes; //指向存储索引的数组 int *reverse; //指向存储反向索引的数组 int count; int capacity;
//私有函数,用户不能调用 void shiftUp(int k) { //如果新添加的元素小于父节点的元素,则进行交换 while (k > 0 && data[indexes[(k - 1) / 2]] > data[indexes[k]]) { swap(indexes[(k - 1) / 2], indexes[k]); reverse[indexes[(k - 1) / 2]] = (k - 1) / 2; reverse[indexes[k]] = k; k = (k - 1) / 2; } }
//也是私有函数,用户不能调用 void shiftDown(int k) { //只要当前节点有孩子就进行循环 while (2 * k + 1 < count) { // 在此轮循环中,data[indexes[k]]和data[indexes[j]]交换位置 int j = 2 * k + 1;
// data[indexes[j]]是data[indexes[j]]和data[indexes[j+1]]中的最小值 if (j + 1 < count && data[indexes[j + 1]] < data[indexes[j]]) { j += 1; }
if (data[indexes[k]] <= data[indexes[j]]) { break; }
swap(indexes[k], indexes[j]); reverse[indexes[k]] = k; reverse[indexes[j]] = j; k = j; } }
public:
MinIndexHeap(int capacity) { data = new Item[capacity]; indexes = new int[capacity]; reverse = new int[capacity]; //初始化reverse数组 for (int i = 0; i < capacity; i++) { reverse[i] = -1; } //计数器,这里索引等于计数器减一 count = 0; this->capacity = capacity;
}
~MinIndexHeap() { delete []data; delete []indexes; delete []reverse; }
int size() { return count; }
bool isEmpty() { return count == 0; }
void insert(int i, Item item) { //防止越界 assert(count <= capacity); assert(i >= 0 && i <= capacity);
data[i] = item; indexes[count] = i; reverse[i] = count; count++;
shiftUp(count - 1); }
//取出最小的data Item extractMin() { //首先要保证堆不为空 assert(count > 0);
Item ret = data[indexes[0]]; swap(indexes[0], indexes[count - 1]); reverse[indexes[count - 1]] = -1; reverse[indexes[0]] = 0; count--; shiftDown(0); return ret; }
//取出最小的data对应的index int extractMinIndex() { assert(count > 0);
//对于外部来说,索引从0开始,所以要减一 int ret = indexes[0]; swap(indexes[0], indexes[count - 1]); reverse[indexes[count - 1]] = -1; reverse[indexes[0]] = 0; count--; shiftDown(0); return ret; }
Item getMin() { assert(count > 0); return data[indexes[0]]; }
int getMinIndex() { assert(count > 0); return indexes[0]; }
bool contain(int i){ assert(i >= 0 && i <= capacity); //reverse数组在构造函数中都初始化为-1, //所以拿-1做比较 return reverse[i] != -1; }
Item getItem(int i) { assert(contain(i)); //对于外部来说,索引从0开始, //对于内部来说,索引从1开始, //所以要加一 return data[i]; }
//修改 index 对应的 data void change(int i, Item newItem) { //防止越界和检查i是否在堆中, //因为有可能已经取出去了 assert(contain(i));
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置 // 之后尝试着shiftUp(j)一下, 再shiftDown(j)一下 //即看看能不能向上或向下移动以保持堆的性质 int j = reverse[i]; shiftUp(j); shiftDown(j);
//先用O(1)的时间找到位置,再用O(lgn)的时间完成 //Shift Up和Shift Down,此时,该函数的时间复杂 //度就是O(lgn)级别的,如果有n个堆操作,总时间 //就是O(n*lgn) // //加入了反向查找后,性能得到了巨大的提升 }
public:
//在控制台打印测试用例 void testPrint() {
//限制:只能打印100个元素以内的堆,因为控制台一行的字符数量有限 if (size() >= 100) { cout << "Fancy print can only work for less than 100 int"; return; }
//限制:只能打印类型是int的堆 if (typeid(Item) != typeid(int)) { cout << "Fancy print can only work for int item"; return; }
cout << "The Heap size is: " << size() << endl; cout << "data in heap: "; for (int i = 0; i < size(); i++) { cout << data[i] << " "; } cout << endl; cout << endl;
int n = size(); int max_level = 0; int number_per_level = 1; while (n > 0) { max_level += 1; n -= number_per_level; number_per_level *= 2; }
int max_level_number = int(pow(2, max_level - 1)); int cur_tree_max_level_number = max_level_number; int index = 0; for (int level = 0; level < max_level; level++) { string line1 = string(max_level_number * 3 - 1, ' ');
int cur_level_number = min(count - int(pow(2, level)) + 1, int(pow(2, level)));
bool isLeft = true;
for (int index_cur_level = 0; index_cur_level < cur_level_number; index++, index_cur_level++) { putNumberInLine(indexes[index], line1, index_cur_level, cur_tree_max_level_number * 3 - 1, isLeft);
isLeft = !isLeft; } cout << line1 << endl;
if (level == max_level - 1) { break; }
string line2 = string(max_level_number * 3 - 1, ' '); for (int index_cur_level = 0; index_cur_level < cur_level_number; index_cur_level++) { putBranchInLine(line2, index_cur_level, cur_tree_max_level_number * 3 - 1); }
cout << line2 << endl;
cur_tree_max_level_number /= 2; } }
private:
void putNumberInLine(int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width + 1) + sub_tree_width;
assert(offset + 1 < line.size());
if (num >= 10) { line[offset + 0] = '0' + num / 10; line[offset + 1] = '0' + num % 10; } else { if (isLeft) line[offset + 0] = '0' + num; else line[offset + 1] = '0' + num; } }
void putBranchInLine(string &line, int index_cur_level, int cur_tree_width) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width + 1) + sub_sub_tree_width;
assert(offset_left + 1 < line.size());
int offset_right = index_cur_level * (cur_tree_width + 1) + sub_tree_width + 1 + sub_sub_tree_width;
assert(offset_right < line.size());
line[offset_left + 1] = '/'; line[offset_right + 0] = '\'; } };
#endif |
Dijkstra.h:
|
#ifndef DIJKSTRA_H #define DIJKSTRA_H
#include "Edge.h" #include "MinIndexHeap.h" #include <iostream> #include <vector> #include <stack> using namespace std;
//Dijkstra 算法实现最短路径 template<typename Graph, typename Weight> class Dijkstra {
private:
Graph &G; //图的引用,即要进行操作的图 int s; //起始顶点 s,s 即 source Weight *distTo; //起始顶点 s 到每一个顶点的当前最短距离 bool *marked; //对已经找到最短路径的顶点进行标识 vector<Edge<Weight>*> from; //经由哪条边到达了当前顶点
public:
Dijkstra(Graph &graph, int s) :G(graph) {
this->s = s; distTo = new Weight[G.V()]; marked = new bool[G.V()];
for (int i = 0; i < G.V(); i++) { //由于不知道 distTo 数组中元素的具体类型, //所以使用模板类型Weight的默认构造函数, //如果指定的模板为 int,会被初始化为 0 distTo[i] = Weight(); marked[i] = false; from.push_back(NULL); }
MinIndexHeap<Weight> ipq(G.V());
// Dijkstra // //对起始顶点 s 到自身的最短距离进行初始化, //如果指定的模板为 int,会被初始化为 0 distTo[s] = Weight(); ipq.insert(s, distTo[s]); marked[s] = true;
//只要最小索引堆不为空,就进行循环 while (!ipq.isEmpty()) { //从最小索引堆中找到当前最短距离最小的顶点 v //此时,distTo[v] 就是起始顶点 s 到顶点 v 的 //最短距离 int v = ipq.extractMinIndex(); marked[v] = true;
//注意:声明迭代器时,前面还要加 typename,表明 //adjIterator 是 Graph 中的类型,而不是成员变量 typename Graph::adjIterator adj(G, v); //对当前顶点 v 的所有相邻顶点依次进行松弛操作 for (Edge<Weight> *e = adj.begin(); !adj.end(); e = adj.next()) { //当前顶点 v 的相邻顶点 w int w = e->other(v); //如果顶点 w 没有被标识,即从起始顶点 // s 到相邻顶点 w 的最短路径还没有找到 if (!marked[w]) { //(1)如果还没有边到达相邻顶点 w //(2)或:"经过"当前顶点 v 到相邻顶点 w 所得到的 //路径小于"不经过"当前顶点 v 到相邻顶点 w 所得到 //的路径,就进行松弛操作 if (from[w] == NULL || distTo[v] + e->wt() < distTo[w]) { distTo[w] = distTo[v] + e->wt(); from[w] = e;
//判断最小索引堆中是否包含顶点 w, //如果包含就更新,否则直接插入 if (ipq.contain(w)) { ipq.change(w, distTo[w]); } else { ipq.insert(w, distTo[w]); } } } } } }
~Dijkstra() { delete []distTo; delete []marked; }
//顶点 s 到顶点 w 的最短距离 Weight shortestPathTo(int w) { assert(w >= 0 && w < G.V()); return distTo[w]; }
//判断顶点 s 到顶点 w 是否有路径, //即判断二者是否连通即可 bool hasPathTo(int w) { assert(w >= 0 && w < G.V()); return marked[w]; }
//找到从顶点 s 到顶点 w 的最短路径的边的组成:通过from数组 //从顶点 w 倒推回去,并存储在栈中,最后再从栈中转存到向量中 void shortestPath(int w, vector<Edge<Weight>> &vec) {
assert(w >= 0 && w < G.V());
stack<Edge<Weight>*> s;
Edge<Weight> *e = from[w];
//直到倒推到起始顶点,对于有向图 //来说,e->v() 即一条边的起点 while (e->v() != this->s) { s.push(e); e = from[e->v()]; } s.push(e);
//只要栈不为空,就将栈顶元素放入 //向量中,并出栈 while (!s.empty()) { e = s.top(); vec.push_back(*e); s.pop(); } }
//打印从顶点 s 到顶点 w 的最短路径 void showPath(int w) {
assert(w >= 0 && w < G.V());
vector<Edge<Weight>> vec; shortestPath(w, vec); for (int i = 0; i < vec.size(); i++) { cout << vec[i].v() << " -> "; if (i == vec.size() - 1) { cout << vec[i].w() << endl; } } } };
#endif |
main.cpp:
|
#include "SparseGraph.h" #include "DenseGraph.h" #include "ReadGraph.h" #include "Dijkstra.h" #include <iostream> using namespace std;
int main() {
string filename = "testG1.txt"; int V = 5;
//稀疏图:通常在实际生活中所处理的图,稀疏图相对更多 SparseGraph<int> g = SparseGraph<int>(V, true); //SparseGraph<int> g = SparseGraph<int>(V, false); ReadGraph<SparseGraph<int>, int> readGraph(g, filename);
cout << "Test Dijkstra:" << endl << endl; Dijkstra<SparseGraph<int>, int> dij(g, 0); for (int i = 1; i < V; i++) { cout << "Shortest Path to " << i << " : " << dij.shortestPathTo(i) << endl;
dij.showPath(i);
cout << "----------" << endl; }
system("pause"); return 0; }
//每一次插入和更新,都使用 logV 的时间复杂度,而整个 //Dijkstra 算法过程中,要对所有的边进行一次遍历,最 //终使得算法的时间复杂度是 O(E*logV) 这个级别的 |
运行一览:

其中,testG1.txt 的内容如下:
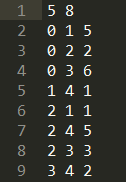
该文件可以分成两个部分:
(1)第一行:两个数字分别代表顶点数和边数
(2)其它行:每一行的前两个数字表示一条边,第三个数字表示权值
【made by siwuxie095】