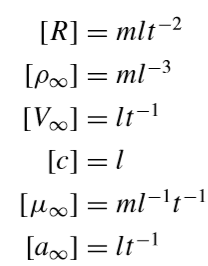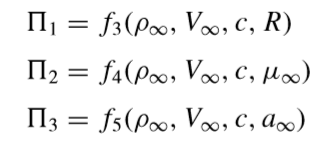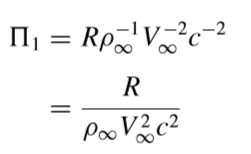目录
量纲分析:白金汉PI定理
在空气动力学中,飞机的空气动力主要由自由来流的密度ρ∞,自由来流数V∞,翼弦长度c,自由来流的粘性系数μ∞以及音速a∞,所以假设我们可以推导出,空气动力大致满足以下这个式子:R = f (ρ∞,V∞,c,μ∞,a∞)。也就是 F(ρ∞,V∞,c,μ∞,a∞,R) = 0。然而不幸的是,对于这个看着就头大的式子,我们需要通过大量的实验来得出他们的关系, 这是项十分庞大的工程。这是我们今天的主角登场了——白金汉PI定理。
我们知道,对于带单位的式子,它的每一个组成部分的单位应该都是一致的,这条定理就是基于这个条件的。我们来看看它是如何大显神威的。在力学中,所有的物理变量都可以用质量,长度以及时间的组合来表达,也就是无论多复杂的式子,最后式子结果都得可以用这三个量纲来表示。我们先从所有变量中挑选三个参数,这三个参数必须能覆盖质量,长度和时间的量纲,也就是(a,b,c表示未知数,那个不认识的希腊字母是参数)能够表示出质量,长度和时间的量纲来。
对R = f (ρ∞,V∞,c,μ∞,a∞)的式子进行分解,
【PS:m是质量的量纲,l是长度量纲,t是时间的量纲。】
在这里,我们选择 ρ∞,V∞,c这三个参数(不妨试试用这三个参数表示质量,长度和时间),我们得到
这里的ρ∞,V∞,c其实可以看成m,l,t,第四个参数呢就可以用前前三个参数来表示。以第一个为例,
方程左边为无量纲,所以方程右边也应该是无量纲的,我们能解出d,b,e的值,我们最终得到:
这里就是,面积,我们可以看成是S,即
,
为空气动力系数
。
相似参数
同理,可推出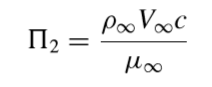
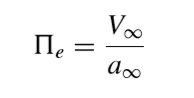
。
这时F(ρ∞,V∞,c,μ∞,a∞,R) = 0就可以变成了 ,这时我们发现,原先有六个参数的式子只剩下了三个,大大简化了计算。我们可以将这个式子换个形式:
,同理我们也可以推出升力系数
和阻力系数
。我们发现,升力系数和阻力系数是关于
和
的函数(在实际中,升力系数和阻力系数还与迎角有关,所以
,
,
表示迎角。当然喽,对于高超音速空气动力学,我们还要考虑热传导系数等),只要
和
相同,升力系数和阻力系数也会相同,所以我们称
和
为相似系数,即两个来流的相似参数相同,则在不考虑翼型的情况下,升力系数和阻力系数也是相同的,这为我们可以用缩小版的模型模拟真实飞机受到的空气动力提供了可能。
最后,感谢白金汉同志拯救我们于眼瞎之中!