[OI学习笔记]Tarjan求强联通分量

背景

　　今天下午我该死地点开了洛谷网校找虐。。。听tarjan全程懵逼。。。于是乎，我查遍的各种资料、博客、b站（我竟然在b站上学习）

　　顺便贴上我认为很有帮助我理解的一个视频：

强联通分量

　　什么是强联通分量？

　　百度百科:

　　有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

　　人话：把一张图的一部分抠出来，使这部分图的每一个节点都能互相通达，并且没有另一个这样的图完全包含它。（单个点也算）

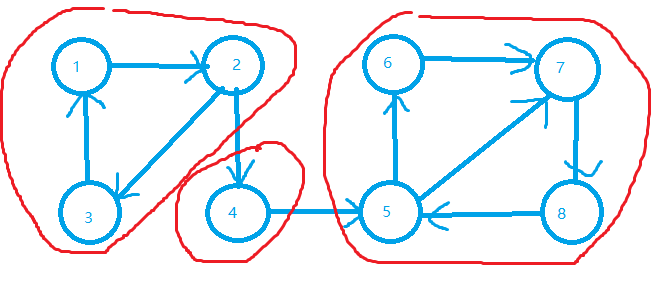
　　比如说下面这张图：（在本篇博文中都以这张图作为样例） 

　　

　　根据定义，{1,2,3}，{4}，{5,6,7,8}都是强联通分量

　　而{5,7,8}不是强联通分量，因为还有比它更大的{5,6,7,8}包含它。

　　

Tarjan算法　　

　　算法的过程实际上就是在图上做DFS。

　　我们把这个图画成树：

　　

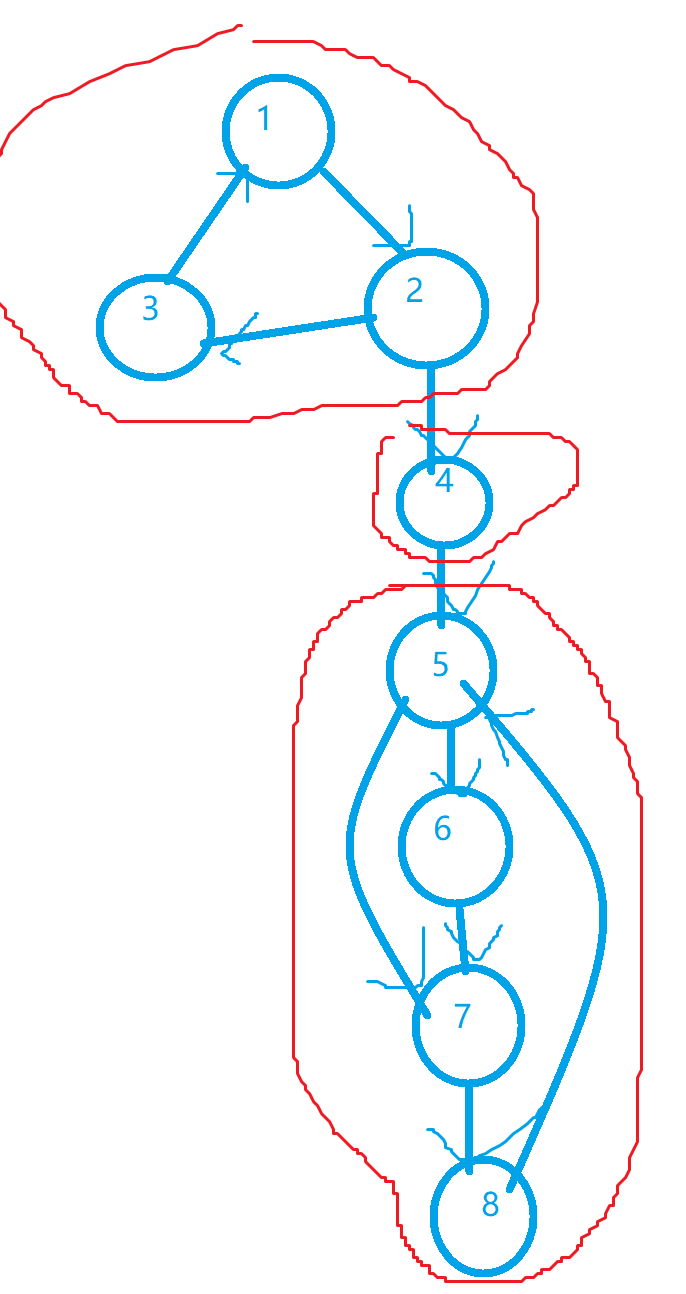
　　这里，我们要定每个点i的两个变量low[i]和dfn[i]：

　　dfn[i]：点i被dfs到的次序，有的人也称之为时间戳

　　low[i]：点i所能向后追溯到的最小的时间戳

　　我们发现：每一个强联通分量都有一个根节点，在这个强联通分量中，根节点的dfn最小

　　由此观之，当一个点的dfn==low时，这个点必是一个强联通分量的根节点，而他的子树中的一个点如果可以dfs到它，那这个点就是他的强联通的一部分！

----------------------------------------分割线--------------------------------------------

　　dfs过程：对于每一个点u：

　　1.初始化dfn[u]=low[u]，将u点入栈

　　2.遍历u的每一个到达的点v：

　　　　1.如点v未访问过，那么就对点v进行dfs，然后更新low[u]=min(low[u],low[v])

　　　　2.如果遍历到的这个点已经被遍历到了，并在栈里，那么直接更新low[u]=min(low[u],dfn[v])

　　3.如果点u的dfn=low（即上面提到的一个强连通分量中dfn最小），那么依次将栈顶元素到点u元素（包括u）出栈并记录。

手算&图解

　　还是手算演示一下过程：(每个点上面的数是dfn,下面的数low)(这里换一张图，前面那张手算太毒瘤了。。。)

　　找到{5}{4}：

　　

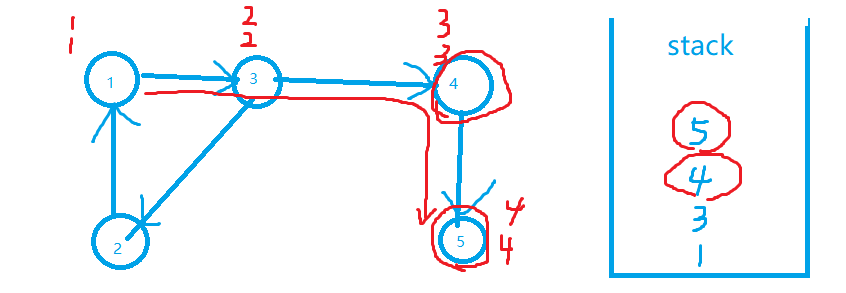
　　遍历到2

　　

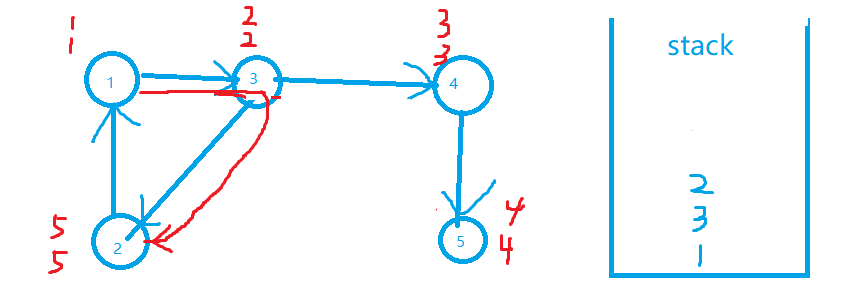
　　注意这里2的low改了：

　　

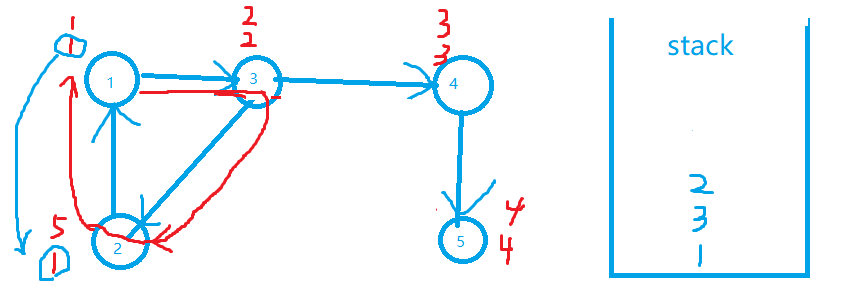
　　最后回到点1发现dfn[1]==low[1],可以确定栈顶到元素1为一个强联通分量：

　　

 代码

　　理解了算法，代码其实也不会复杂，，，这里给出代码，如果有错误请各位dalao指点：

#include<cstdio>
#include<algorithm>
#include<stack>
#include<cstring>
using namespace std;

const int MAX=233;
int m,n;
int first[MAX];

struct edge{//check
    int u,v,next;
}e[10086];

int cnt=0;
void insert(int u,int v){
    ++cnt;e[cnt].u=u;e[cnt].v=v;e[cnt].next=first[u];first[u]=cnt;
}

int dfn[MAX]={0},low[MAX]={0},ins[MAX]={0};
stack<int> s;
int tot=0;
void tarjan(int u){
    dfn[u]=low[u]=++tot;
    s.push(u);
    ins[u]=1;
    for(int i=first[u];i!=-1;i=e[i].next){//ckeck
        int v=e[i].v;
        if(dfn[v]==0){//没搜过 
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(ins[v]){//已搜过&在队里 
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(dfn[u]==low[u]){
        int fa=0,van[MAX];
        while(s.top()!=u){
            van[++fa]=s.top();
            ins[s.top()]=0;
            s.pop();
        }
        s.pop();
        ++fa;van[fa]=u;
        for(int i=1;i<=fa;i++){
            printf("%d ",van[i]);
        }
        printf("是一个scc
");
    }
}

int main(){
    memset(first,-1,sizeof(first));
    scanf("%d%d",&n,&m);
    int x,y;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
        insert(x,y);
    }
    for(int i=1;i<=n;i++){
        if(dfn[i]==0){
            tarjan(i);
        }
    }
    return 0;
} 

 我太弱了。。。竟然研究了一个晚上才懂。。。QwQ