背景
(第一次写博客,没什么经验,另外图画的很丑,请多包涵)
关于存储图的方法,今天研究了一下,终于把邻接表弄懂了。。。
一张有向图图有N个点,M条边,从点u到点v的边表示为(u,v),每条边又有相应的边权w
举个栗子,更方便演示。就像下面这幅图:
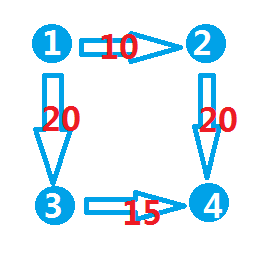
我们第一行输入n,m 之后的每一行输入一条边的 u v w,于是就输入这个:
4 4 1 2 10 1 3 20 2 4 20 3 4 15
那么现在,应该考虑用一个什么数据结构来存储这张图呢?
邻接矩阵
首先,我们想到的是用一个二维数组来存储所有的边,像这样:
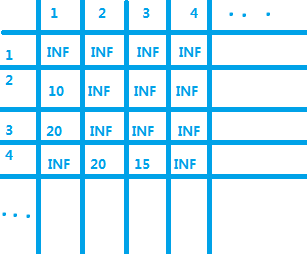
先把所有边都设成最大值,然后输入一条就把对应的s[u][v]改回来
邻接表
邻接矩阵简单是简单,但是空间复杂度是O(n^2)的,容易爆内存。
这时,就要用到邻接表。对于每一个点,可以用一个链表来存储由这个点出发的每一条边,像这样:
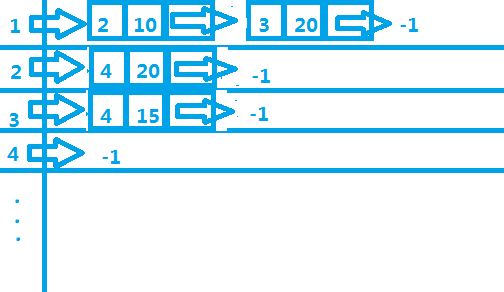
具体实现:
方法一:数组模拟链表
声明数组u,v,w,first,next,first[i]表示存储以i开头的边的链表表头,next[i]表示第i行指向的下一条边
1)初始化:把first全部赋值为-1,如果一条边指向-1,那么就表示这条边不再指向任何一条边。
2)更新:读入第i行uvw,next[i]=first[u[i]],first[u[i]]=i,即把这条边指向当前表头,再把这条边设为表头
3)遍历
int main(){ scanf("%d %d",&n,&m); int i; for(i=1;i<=n;i++) first[i]=-1; for(i=1;i<=m;i++){ scanf("%d %d %d",&u[i],&v[i],&w[i]); //插入 next[i]=first[u[i]]; first[u[i]]=i; } int k; for(i=1;i<=n;i++){ k=first[i]; while(k!=-1){ printf("%d %d %d ",u[k],v[k],w[k]); k=next[k]; } } return 0; }
方法二:动态数组
这个比较简单,不做详细解释,就是用一个可自由变长的神奇数组存储链表,要#include<vector>和引用命名空间std
代码:
#include<vector> #include<cstdio> #define MAXN 10000 using namespace std; struct edge{ int v,w; }; vector <edge> e[MAXN]; inline void insert(int _u,int _v,int _w){ e[_u].push_back({_v,_w}); //如果是无向图,则要改为 e[u].push_back({v,w});e[v].push_back({u,w}); } int n,m; int main(){ scanf("%d%d",&n,&m); int u,v,w; for(int i=1;i<=m;i++){ scanf("%d%d%d",&u,&v,&w); insert(u,v,w); } for(int i=1;i<=n;i++){ for(int j=0;j<e[i].size();j++){ printf("%d %d %d ",i,e[i][j].v,e[i][j].w); } } return 0; }
P.S.上述两种方法对于无向图,反过来再赋一遍即可。