[OI学习笔记]排列组合&二项式定理

    这几天都在准备初赛，所以没有时间来更新博客了，等缓过这几天来吧。。。心好累。。。

    9月份以来好多笔记都没发，慢慢来吧。

---

　　

排列与组合

绪论：加法原理、乘法原理

　　　　　　1）加法原理：要完成某件任务，分为n种方法，则方案总数为n

　　　　　　2）乘法原理：要完成某件任务，分为n个步骤，完成第一个步骤有m1种方法，完成第二个步骤有m2种方法，……，完成第n个步骤有mn种方法，则完成整个任务的方案总数为m1*m2*……*mn

排列数

　　　　　　1）在m个元素中取n个进行排列（理解排列，允许相同n个元素而顺序不同的几个排列同时存在）的方案总数，记作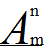  （不知道TinyMCE编辑器怎么插入上下标，只能贴图了）

　　　　　　2）要在m个元素中选出n个进行排列的方案：首先在m个中选出第一个元素，有m中选法；然后在(m-1)个元素中选第二个，有(m-1)中选法；……；以此类推，最后在(m-n+1)个元素中选出第n个，有(m-n+1)种方法。这些过程的关系是一步接一步的，显然符合乘法原理。

　　　　　　3）所以：

　　　　　　   可以变形为：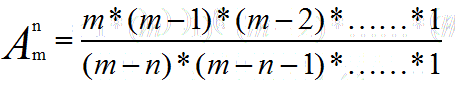

               即：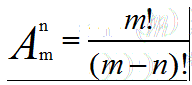

　　　　　　4）当m=n时，即在m个元素中选m个时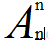，叫做全排列，A(n,n)=n!  ；　　

组合数

　　　　　　1）不考虑顺序，即不管元素的顺序如何，都是同一个组合

　　　　　　2）在m个元素中选n个的组合数，写作或C(m,n)

 　　　　为了方便表达，下面把排列与组合数统一写成A(m,n)&C(m,n)

　　　　　　3）C(m,n)怎么求呢？可以用A(m,n)来重新思考：

　　　　　　　　求A(m,n)的原理可以理解为：先从m个中取n个，不考虑顺序（即C(m,n)），然后再从这n个中进行排列（即A(m,n)）。

　　　　　　　　所以：A(m,n)=C(m,n)*A(n,n)

　　　　　　　　变形一下：C(m,n)=A(m,n)/A(n,n)   //偷懒，就不写成分数形式了

　　　　　　　　即：A(m,n)=m!/(m-n)!n!

　　　　　　4)组合数与杨辉三角之间的关♂系♂

　　　　　　　　C1 0=1，C1 1=1,C2 0=1;C2 1=2,……

　　　　　　　　通过观察可以发现，组合数似乎与杨辉三角有什么关系

　　　　　　　　

　　　　　　　　那岂不是可以用杨辉三角来快速求组合数了？

　　　　　　　　

二项式定理

　　　　

　　　　　　1）二项式定理为：

　　　　　　　　(a+b)ⁿ =∑ ⁿ_r=0 C(n,r)a^n-r b^r (n和r分别是上下标，这里打不出来)

　　　　　　2）即(a+b)ⁿ ，a^n-r b^r 项的系数为C(n,r)

　　　　　　3）由于C(n,r)=C(n,n-r)，所以a^n-r b^r 和a^r b^n-r 项的系数相同

　　　　　　4）也和杨辉三角有关：

　　　　　　　　(a+b)¹ =1a+1b----------------------------------------1 1

　　　　　　　　(a+b)² =1a²+2ab+1b² ---------------------------------1 2 1

　　　　　　　　(a+b)¹ =1a³+3a²b+3ab²+1b³ ---------------------------1 3 3 1

 　　　　　　　　　……                                                           　　　　　　　　　　   ……