
【问题描述】
栈是一种强大的数据结构,它的一种特殊功能是对数组进行排序。例如,借助一个栈,依次将数组1,3,2按顺序入栈或出栈,可对其从大到小排序:
1入栈;3入栈;3出栈;2入栈;2出栈;1出栈。
在上面这个例子中,出栈序列是3,2,1,因此实现了对数组的排序。
遗憾的是,有些时候,仅仅借助一个栈,不能实现对数组的完全排序。例如给定数组2,1,3,借助一个栈,能获得的字典序最大的出栈序列是3,1,2:
2入栈;1入栈;3入栈;3出栈;1出栈;2出栈。
请你借助一个栈,对一个给定的数组按照出栈顺序进行从大到小排序。当无法完全排序时,请输出字典序最大的出栈序列。
【输入格式】
输入共行。
第一行包含一个整数,表示入栈序列长度。
第二行包含个整数,表示入栈序列。输入数据保证给定的序列是到n的全排列,即不会出现重复数字。
【输出格式】
仅一行,共个整数,表示你计算出的出栈序列。
【样例输入】
3
2 1 3
【样例输出】
3 1 2
【样例解释】
这回山里有座塔。
【数据规模与约定】
对于30%的数据,1<=N<=10^3。
对于60%的数据,1<=N<=10^5。
对于100%的数据,1<=N<=10^6。
题解:感觉自己的代码有种超时的即视感,然而并没有。先找最大的,前面的都入栈。然后找第二大,如果在栈顶,出栈,如果没有,比较栈顶元素和maxn(没入栈的元素)谁大,如果栈顶元素大,出栈,反之将在maxn之前的元素全部入栈,继续重复前面操作。直到栈空。

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #define N 1000100 using namespace std; int n,top(0),maxn; int a[N],zh[N]; bool f[N]={0}; void xx() { while (f[maxn]) maxn--; while (zh[top]>maxn&&top) { printf("%d ",zh[top]); top--; while (f[maxn]) maxn--; } } int main() { freopen("haha.in","r",stdin); freopen("haha.out","w",stdout); scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%d",&a[i]); maxn=n; for (int i=1;i<=n;i++) { if (a[i]!=maxn) zh[++top]=a[i],f[a[i]]=1; if (a[i]==maxn) { f[maxn]=1; printf("%d ",a[i]); xx(); } } while (top) { printf("%d ",a[top]); top--; } fclose(stdin); fclose(stdout); return 0; }

【问题描述】
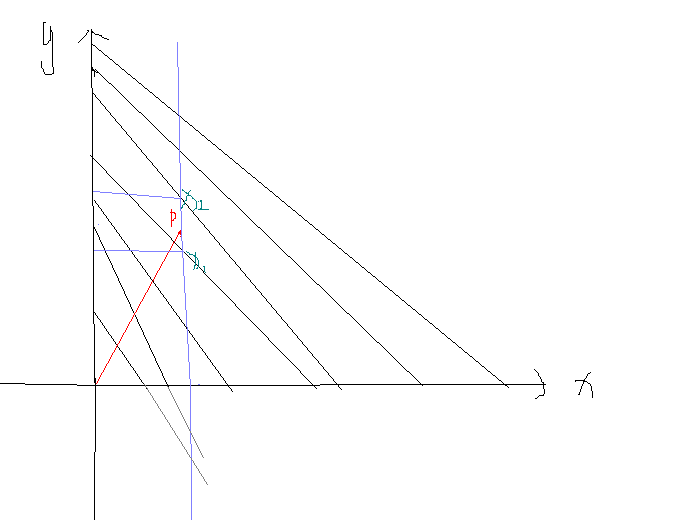
小Q对计算几何有着浓厚的兴趣。他经常对着平面直角坐标系发呆,思考一些有趣的问题。今天,他想到了一个十分有意思的题目:
首先,小Q会在轴正半轴和轴正半轴分别挑选个点。随后,他将轴的点与轴的点一一连接,形成条线段,并保证任意两条线段不相交。小Q确定这种连接方式有且仅有一种。最后,小Q会给出个询问。对于每个询问,将会给定一个点,请回答线段OP与条线段会产生多少个交点?
小Q找到了正在钻研数据结构的你,希望你可以帮他解决这道难题。
【输入格式】
第行包含一个正整数,表示线段的数量;
第行包含个正整数,表示小Q在轴选取的点的横坐标;
第行包含个正整数,表示小Q在轴选取的点的纵坐标;
第4行包含一个正整数,表示询问数量;
随后行,每行包含两个正整数,表示询问中给定的点的横、纵坐标。
【输出格式】
共行,每行包含一个非负整数,表示你对这条询问给出的答案。
【样例输入】
3
4 5 3
3 5 4
2
1 1
3 3
【样例输出】
0
3
【样例解释】
然后塔里啥都没有。
【数据规模与约定】
对于50%的数据,1<=n,m<=2*10^3。
对于100%的数据,1<=n,m<=2*10^5,坐标范围<=10^8。
题解:由于n条线段互不相交,因此将x和y从小到大排序,一一对应形成线段。二分答案,若此时点P与原点形成的线段与此时的第mid条线段相交,则一定与在mid之前的线段相交。判断是否相交时,可以将P点的横坐标第mid条直线的解析式中求出y来,将y与P点的纵坐标进行比较,若y比P点的纵坐标大,说明两线段相交,反之则不相交。

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cmath> #define N 200100 #define ll long long using namespace std; int n,m,ans; double x[N],y[N]; bool check(int k,double x1,double y1) { if (k==0) return 0; double Y=-y[k]/x[k]*x1+y[k];//求把此时的横坐标代入第k条线段对应的纵坐标 return Y<y1; } int main() { freopen(".in","r",stdin); freopen(".out","w",stdout); scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%lf",&x[i]); for (int i=1;i<=n;i++) scanf("%lf",&y[i]); sort(x+1,x+n+1);//小的x对应小的y,保证线段不相交 sort(y+1,y+n+1); scanf("%d",&m); for (int i=1;i<=m;i++) { double xx,yy; scanf("%lf%lf",&xx,&yy); int l=0,r=n; while (l<=r) { int mid=(l+r)>>1; if (check(mid,xx,yy)) ans=mid,l=mid+1; else r=mid-1; } cout<<ans<<endl; } fclose(stdin); fclose(stdout); return 0; }
