一、题目
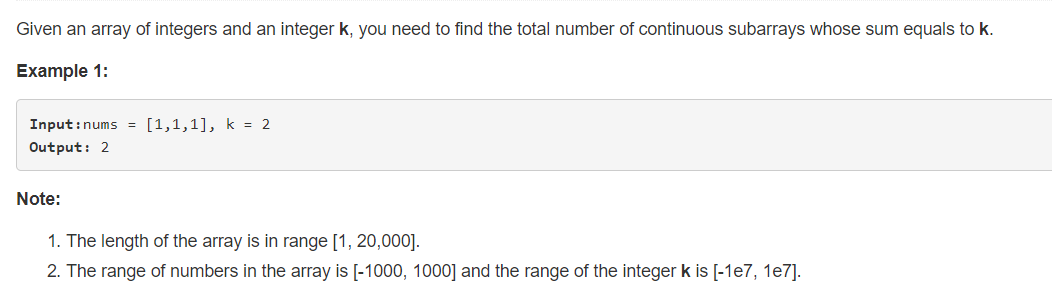
1、审题
2、分析
给定一个整形数组。若存在连续的序列相加和为 k ,统计这样的序列的个数。
二、解答
方法一、
时间复杂度: O(N^2),空间复杂度:O(1)
① 将所给数组 nums,连续元素相加。 nums[i] 代表下标 i 及i之前的元素之和。
② 采用 count 记录满足的序列个数。
③ 采用循环遍历数组 nums,若 nums[i] == K。 则 count++。 采用内循环,若 nums[j] - nums[i] == k ,则 count++
④ 返回 count
public int subarraySum(int[] nums, int k) { int count = 0; for (int i = 1; i < nums.length; i++) nums[i] += nums[i - 1]; for (int i = 0; i < nums.length; i++) { if(nums[i] == k) count++; for (int j = i + 1; j < nums.length; j++) { if(nums[j] - nums[i] == k) count++; } } return count; }
方法二、
采用一个 Map 存储。 key=sum, value=count;
时间复杂度:O(N); 空间复杂度:O(N)
public int subarraySum2(int[] nums, int k) { int sum = 0, result = 0; HashMap<Integer, Integer> preSum = new HashMap<>(); preSum.put(0, 1); for (int i = 0; i < nums.length; i++) { sum += nums[i]; result += preSum.getOrDefault(sum - k, 0); preSum.put(sum, preSum.getOrDefault(sum, 0) + 1); } return result; }