一、题目
1、审题
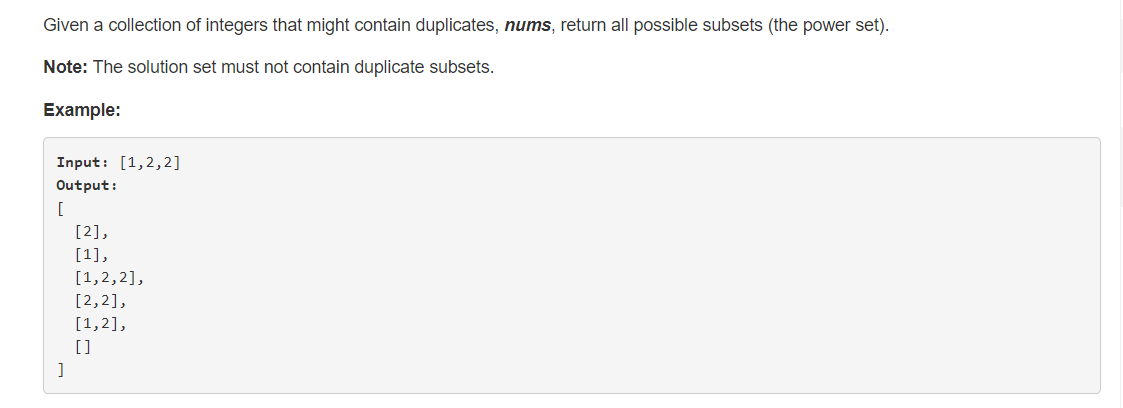
2、分析
给出一个可能有重复数值的整形数组,求其所有的子集合数组。
二、解答
1、思路:
方法一、
采用递归的方法将所有集合放在一个 List 中;
去重所用的公式: if(i > start && nums[i] == nums[i-1]) continue;
public List<List<Integer>> subsetsWithDup(int[] nums) { List<List<Integer>> resultList = new ArrayList<List<Integer>>(); List<Integer> targetList = new ArrayList<>(); Arrays.sort(nums); helper(resultList, targetList, nums, 0); return resultList; } private void helper(List<List<Integer>> resultList, List<Integer> targetList, int[] nums, int start) { resultList.add(new ArrayList<>(targetList)); for (int i = start; i < nums.length; i++) { if(i > start && nums[i] == nums[i-1]) // 子集合去重 continue; targetList.add(nums[i]); helper(resultList, targetList, nums, i+1); targetList.remove(targetList.size() - 1); } }
方法二、
将数组排序,采用循环向 resultList 中添加子集合。
public List<List<Integer>> subsetsWithDup2(int[] nums) { List<List<Integer>> resultList = new ArrayList<List<Integer>>(); resultList.add(new ArrayList<Integer>()); Arrays.sort(nums); int startIndex = 0; int size = 0; for (int i = 0; i < nums.length; i++) { // 若 nums[i] == nums[i-1],则为了避免重复,从上一步添加的 list 下标开始 startIndex = (i >= 1 && nums[i] == nums[i-1] ? size: 0); size = resultList.size(); for (int j = startIndex; j < size; j++) { List<Integer> targetList = new ArrayList<Integer>(resultList.get(j)); targetList.add(nums[i]); resultList.add(targetList); } } return resultList; }