摘自: https://www.cnblogs.com/DSNFZ/articles/7623522.html
https://blog.csdn.net/dm_vincent/article/details/7655764
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
首先我们给出并查集(union-find)的api:

在《algorithm》书中,对与uf的应用直接给出了代码,但是其中find和union方法并没有直接实现,而是空着的。书中代码如下:
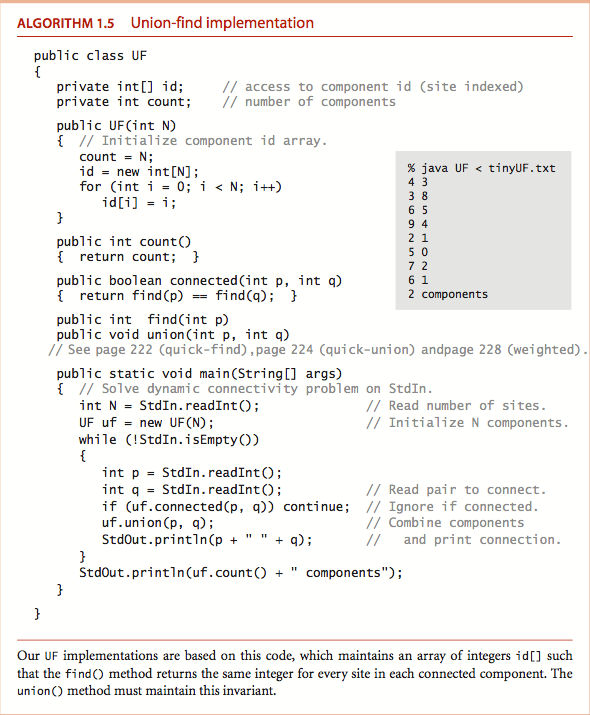
注意:这里看见有一个StdIn的类作为类似于输入流的作用,这个在java中是不存在的,这是这本书自己构造的一个类。相信以后在这本书中也会有类似的部分,可以在网上找到其中的具体实施代码,我会发送出来的。
为什么不直接实现find和union方法呢,这里会考虑到数据结构和算法复杂度的问题。
我们将其分为:quickunion,quickfind,weightedquickunion,weightedquickunion with path compression;
1)Quick-Find
其中判断p和q两个元素是否连接便是让两个元素的id[]相同。
此时,find()便是直接返回id[p]的值
而union()便是将连接的两个集合的id[]变为一致:当然,我们首先要判断她们是不是已经连接;
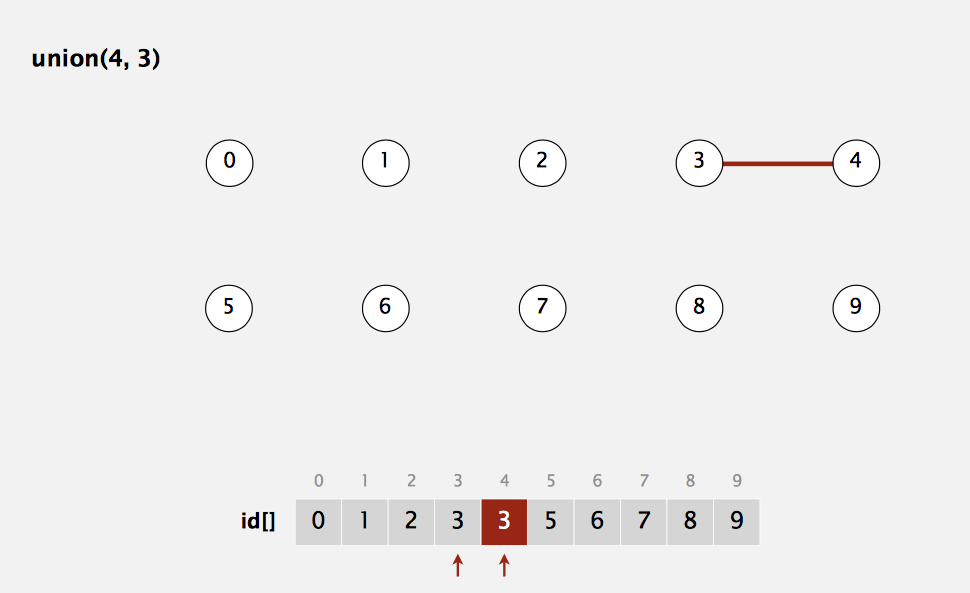
由上图便可看出,我们union(3,4),得到两者的id[]相同,即id[3]=id[4]=3(id值为连接的集合包含的任意一个数);
得到的代码如下:
package unionFind;
public class QuickFindUF {
private int id[];
private int count;
public QuickFindUF(int N){
count=N;
id=new int[N];
for(int i=0;i<N;i++){
id[i]=i;
}
}
public int count(){
return count;
}
public boolean connected(int p,int q){
return find(p)==find(q);
}
public int find(int p){
return id[p];
}
public void union(int p,int q){
int pid=find(p);
int qid=find(q);
if(pid==qid)return;
for(int i=0;i<id.length;i++){
if(id[i]==pid)id[i]=qid;
}
count--;
}
}
2)Quick-Union
Quick-Union的结构如下图所示:

即每一个结点的id为上一个结点。而根节点便是root=id[root];
判断两个元素是否连接则是判断两个元素的根(root)是否相同。
find()则为找到元素的根节点;
union(p,q)即将p的根节点与q的根节点连接。
代码实现如下:
package unionFind;
public class QuickUnionUF {
private int id[];
private int count;
public QuickUnionUF(int N){
id=new int[N];
count=N;
for(int i=0;i<N;i++){
id[i]=i;
}
}
public int count(){
return count;
}
public int find(int i){
while(i!=id[i]){i=id[i];}
return i;
}
public void union(int p,int q){
if(find(p)==find(q))return;
id[find(p)]=find(q);
count--;
}
public boolean connected(int p,int q){
return find(p)==find(q);
}
}
3)Weighted Quick-Union
当然,我们如果胡乱的将根节点相互连接,会导致这个树的结构非常糟糕,比如:

我们可以看到这个树的结构非常非常糟糕。
为了避免这个情况,我们记录树的大小,并且总是将小的树连接到大的树:

使用这种方法可以很大程度的优化树的结构,例如上图的树我们可以变为:

具体实现代码如下:
package unionFind;
public class WeightedQuickUnionUF {
private int id[];
private int count;
private int sz[];
public WeightedQuickUnionUF(int N){
count=N;
id=new int[N];
sz=new int[N];
for(int i=0;i<N;i++){
id[i]=i;
sz[i]=1;
}
}
public int find(int p){
while(p!=id[p])p=id[p];
return p;
}
public void union(int p,int q){
int pid=find(p);
int qid=find(q);
if(qid==pid)return ;
if(sz[pid]<sz[qid]){
id[pid]=qid;
sz[qid]+=sz[pid];
}
else{
id[qid]=pid;
sz[pid]+=sz[qid];
}
count--;
}
public int count(){
return count;
}
public boolean connected(int p,int q){
return find(p)==find(q);
}
}
4)Weighted Quick-Union with Path Compression
最优情况下,我们希望所有的节点都直接连接到根节点上,但是又不希望像QuickUnion那样大量修改连接,这时,我们可以在检查节点的同时将它与根节点直接连接。
例如,我们对下列并查集进行union(7,3);

在采取最优算法下,结果如下:
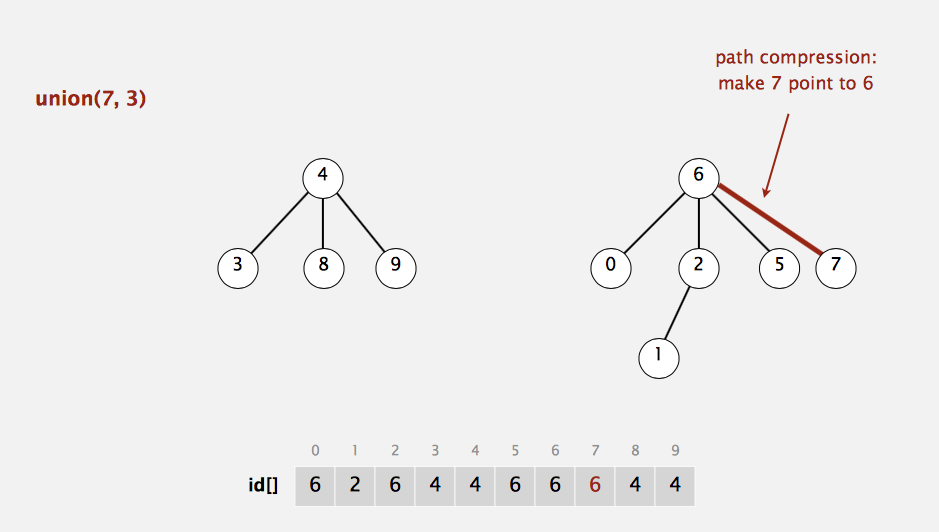
可以看出,我们将遍历到的节点都直接与根节点直接连接,这一切只需要在find内的循环进行修改就可以实现。
具体的代码如下:
package unionFind;
public class WeightedQuickUnionUFWPC {
private int id[];
private int count;
private int sz[];
public WeightedQuickUnionUFWPC(int N){
count=N;
id=new int[N];
sz=new int[N];
for(int i=0;i<N;i++){
id[i]=i;
sz[i]=1;
}
}
public int find(int p){
int root=p;
while(root!=id[root])root=id[root];
while(p!=root){
int x=p;
id[x]=root;
p=id[p];
}
return root;
}
public void union(int p,int q){
int pid=find(p);
int qid=find(q);
if(qid==pid)return ;
if(sz[pid]<sz[qid]){
id[pid]=qid;
sz[qid]+=sz[pid];
}
else{
id[qid]=pid;
sz[pid]+=sz[qid];
}
count--;
}
public int count(){
return count;
}
public boolean connected(int p,int q){
return find(p)==find(q);
}
}
这四种方法能够适应不同的情况,但是对于算法复杂度来说,这四种方法就会有很大的差别:
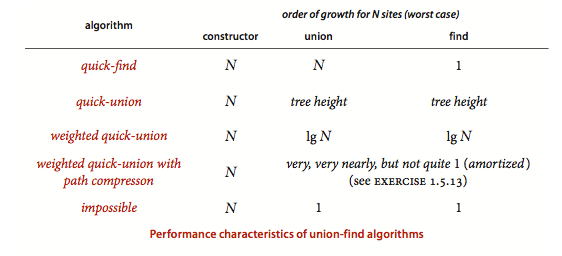
对于每一项的得出,《algorithm》给出了很详细的解释,我希望自己能够有时间写一篇文章来细讲一下。(别说了。感觉还有好多坑没填)
