算法的概念:
算法是计算机处理信息的本质没,因为计算机程序本质上是一个算法来告诉计算机确切的步骤来执行一个指定的任务,一般的,当算法在处理信息时,会从输入设备或数据的存储地址读取数据,把结果写入输出设备或者某个存贮地址以供以后再调用。
算法是独立存在的一种解决问题的方法和思想。
对于算法而言,实现的语言并不重要,重要的是思想。
算法的五大特性
1.输入:算法具有0个或多个输入
2.输出:算法至少有一个或多个输出
3.有穷性:算法在有限的步骤之后会自动结束而不会五险循环,并且每一步骤可以在可接受的时间内完后。
4.确定性:算法中的每一步都有确定的含义,不会出现二义性
5.可行性:算法的每一步都是可行的,也就是说每一步都能够执行有限的次数完成
如果a+b+c=1000,且a^2+b^2=c^2(a,b,c为自然数),如何求出所有a,b,c可能得组合?
枚举法(一个一个列举)
在python中:
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
for c in range(0,1001):
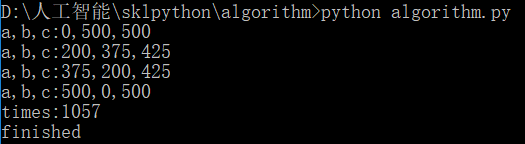
if a**2+b**2 == c**2 and a+b+c==1000:
print("a,b,c:%d,%d,%d"%(a,b,c))
end_time = time.time()
print("times:%d"%(end_time-start_time))
print("finished")
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
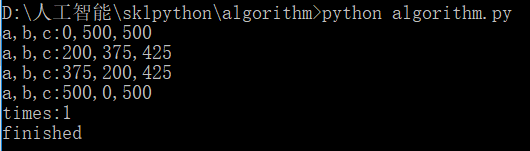
c = 1000-a-b
if a**2+b**2 == c**2:
print("a,b,c:%d,%d,%d"%(a,b,c))
end_time = time.time()
print("times:%d"%(end_time-start_time))
print("finished")
一:时间复杂度与大o表示法:
我们假定计算机执行算法每一个基本操作的时间是固定的一个时间单位,那么有多少基本草最就代表会花费多少时间单位,算法 对于不同的机器环境而言,确切的单位时间是不同的,但是对于算法进行多少个基本操作(即花费多少时间单位)在规模数量级上却是相同的,由此可以忽略机器环境而客观的反应算法的时间效率。
对于算法的时间效率,我们可以用“大o记法”来表示
“大o记法”:对于单调的整数函数f,如果存在一个整数函数g和实常数c>0,使的对于充分大的n总有f(n)<=c*g(n),就是说函数g是f的一个渐进函数(忽略常数)记为f(n)=O(g(n)).也就是说,在趋向无穷的极限意义下,函数的增长速度收到函数g的约束,亦即函数f与函数g的特征相似。
“时间复杂度”:假设存在函数g,使的算法A处理规模为n的问题实例所用的时间为T(n) = O(g(n)),则称O(g(n))为算法A的渐进时间复杂度,简称时间复杂度,记为T(n)
按照实例1来计算时间复杂度
a+b+c=1000(计算步骤)
T(1000) = 1000 * 1000 * 1000 * 2
a+b+c=2000(计算步骤)
T(2000)= 2000 * 2000 * 2000 * 2
a+b+c=n(计算步骤)
T(n)= n * n * n * 2
g(n) = n^3 (大o表示法)
T (n)= k*g(n)
2n^2还是100n^2 这两个函数是一个量级
二:最坏时间复杂度与计算规则
分析算法时,存在几种可能得考虑:
算法完成工作最少需要多少基本操作,叫做最优时间复杂度
算法完成工作最多需要多少基本操作,叫做最坏时间复杂度
算法完成工作平均需要多少基本操作,叫做平均时间复杂度
对于最优时间复杂度,其价值不大,因为他没有提供什么有用信息,其反应的知识最乐观最理想的情况,没有参考价值。
对于最坏时间复杂度,提供了一种保障,表名算法在此程度的基本操作中一定能完成。
对于平均时间复杂度,是对算法的一个全面评价,因此它完整的反应了这个算大的性质,但另一方面,这种很亮并没有保障,不是每个计算都能在这个基本操作内完成,而且,对于平均情况的计算,也会因为应用算法的实例分布可能并不均匀而难以计算。
因此,我们主要关注算法的最坏情况,亦即最坏时间复杂度。
时间复杂度的几条基本计算规则
1.基本操作,即只有常数项,认为其时间复杂度为O(1)
2.顺序结构,时间复杂度安加法进行计算
3.循环结构,时间复杂度按乘法进行计算
4.分支结构,时间复杂度取最大值
5.判断一个算法的效率时,旺旺只需要关注操作数量的最高次项,其它次要项和常数项可以忽略
6.在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度。
常见时间复杂度与大小关系
执行次数函数举例 阶 非正式术语
12 O(1) 常数阶
2n+3 O(n) 线性阶
3n^2+2n+1 O(n^2) 平方阶
5log2^n+20 O(logn) 对数阶
2n+3log2^n+19 O(nlogn) nlogn阶
6n^3+2n^2+3n+5 O(n^3) 立方阶
2^n O(2^n) 指数阶
所消耗的时间从小到大
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(n!)<O(n^n)