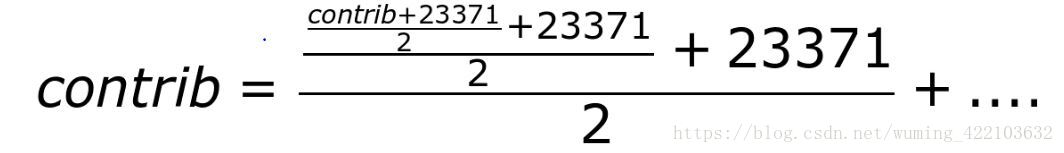Scheduler里面这个负载的概念可能被误解为cpu占用率,但是在调度里面这个有比较大的偏差。scheduler不使用cpu占用率来评估负载,而是使用runnable_time_avg,即平均运行时间来评估负载。sheduler也分了几个层级来计算负载:
- entity级负载计算:update_load_avg()
- cpu级负载计算:update_cpu_load_active()
- 系统级负载计算:calc_global_load_tick()
第一个是调度实体的load,即sched_entity的load,根据PELT算法实现的,算法逻辑如下:
PELT(Per Entity Load Tracing)算法概述
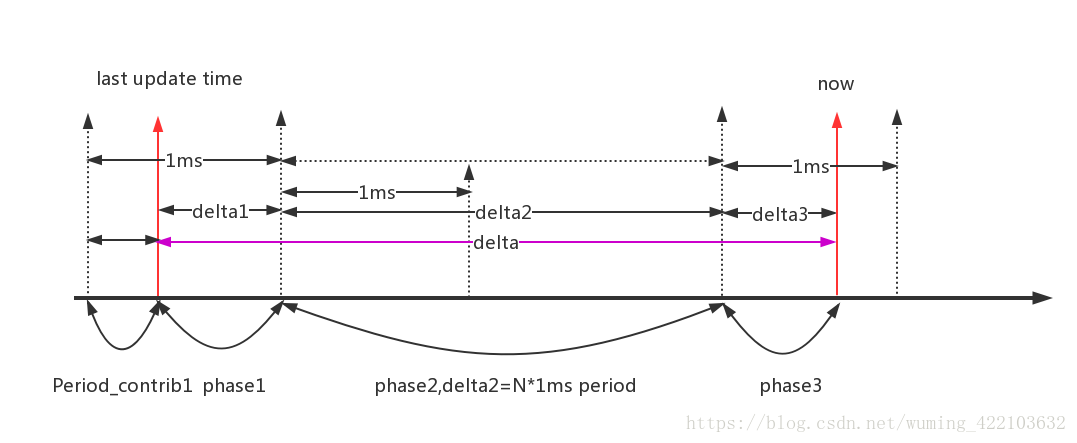
从上面示意图可以看到,task runtime是delta=delta1+delta2+delta3之和
- delta数值依赖真实task的运行时间,是总的运行时间
- last update time是task load的上次更新的最后时间(第一个红色箭头)
- now是task load更新的当前时间(第二个红色箭头)
- 1ms表示1024us的颗粒度,由于kernel对于除法效率较低和不能使用小数位,所以1ms直接转化为1024us,好做乘法和位移运算,真的很巧妙
示意图的目的就是追踪三个时间段(phase1/phase2/phase3)的load,来计算now时刻的load,周而复始.
###PELT算法
#####Phase1阶段怎么计算load
- 计算delta1的period:
delta1 = 1024 - Period_contrib1 (< 1024us) - load_sum被刻度化通过当前cpu频率和se的权重:
delta1 = delta1 * scale_freq
load_sum += weight*delta1 - load_util被cpu的capacity刻度化
util_sum += scale_cpu *delta1;
#####Phase2阶段怎么计算load的:
- 计算delta2的period
periods = delta2 / 1024(即存在有多少个1ms) - 衰减phase1的load
load_sum += decay_load(load_sum , periods + 1)
util_sum += decay_load(util_sum , periods + 1) - 衰减阶段phase2的load
load_sum += __contrib(periods) * scale_freq
util_sum += __contrib(periods) * scale_freq * scale_cpu
#####Phase3计算怎么计算load:
- 计算剩余周期(<1ms,<1024us)
period_contrid2 = delta3 % 1024 - load_sum被当前权重和频率刻度化
load_sum += weight * scale_freq * period_contrib2 - util_sum被当前频率和当前cpu capacity刻度化
util_sum += scale_cpu * scale_freq * period_contrib2
上面是这个算法的精髓以及思路,下面讲解decay_load和__contrib怎么计算的
######decay_load:
对于每一个period(大小为LOAD_AVG_PERIOD=32ms),这个load将衰减0.5,因此根据当前period,load被衰减方式如下:
- load = (load >> (n/period)) * y^(n%period)
- 并且y^(n%period) * (2^32 - 1) 可以看成runnable_avg_yN_inv[n]的数值
在kernel中查表即可:
/* Precomputed fixed inverse multiplies for multiplication by y^n */
static const u32 runnable_avg_yN_inv[] = {
0xffffffff, 0xfa83b2da, 0xf5257d14, 0xefe4b99a, 0xeac0c6e6, 0xe5b906e6,
0xe0ccdeeb, 0xdbfbb796, 0xd744fcc9, 0xd2a81d91, 0xce248c14, 0xc9b9bd85,
0xc5672a10, 0xc12c4cc9, 0xbd08a39e, 0xb8fbaf46, 0xb504f333, 0xb123f581,
0xad583ee9, 0xa9a15ab4, 0xa5fed6a9, 0xa2704302, 0x9ef5325f, 0x9b8d39b9,
0x9837f050, 0x94f4efa8, 0x91c3d373, 0x8ea4398a, 0x8b95c1e3, 0x88980e80,
0x85aac367, 0x82cd8698,
};
#define LOAD_AVG_PERIOD 32
#define LOAD_AVG_MAX 47742 /* maximum possible load avg */
#define LOAD_AVG_MAX_N 345 /* number of full periods to produce LOAD_AVG_MAX */
其实现代码如下:
/*
* Approximate:
* val * y^n, where y^32 ~= 0.5 (~1 scheduling period)
*/
static __always_inline u64 decay_load(u64 val, u64 n)
{
unsigned int local_n;
if (!n)
return val;
else if (unlikely(n > LOAD_AVG_PERIOD * 63))
return 0;
/* after bounds checking we can collapse to 32-bit */
local_n = n;
/*
* As y^PERIOD = 1/2, we can combine
* y^n = 1/2^(n/PERIOD) * y^(n%PERIOD)
* With a look-up table which covers y^n (n<PERIOD)
*
* To achieve constant time decay_load.
*/ /*LOAD_AVG_PERIOD = 32*/
if (unlikely(local_n >= LOAD_AVG_PERIOD)) {
val >>= local_n / LOAD_AVG_PERIOD;
local_n %= LOAD_AVG_PERIOD;
}
/*正好符合:load = (load >> (n/period)) * y^(n%period)计算方式*/
val = mul_u64_u32_shr(val, runnable_avg_yN_inv[local_n], 32);
return val;
}
__contrib:
- if period <= LOAD_AVG_PERIOD(32ms, 32 * 1024us)
load = 1024 + 1024y + 1024y^2 + ……+1024*y^period - if period > LOAD_AVG_MAX_N(345ms)
load = LOAD_AVG_MAX (47742) - if period∈(32, 345],即每个LOAD_AVG_PERIOD周期衰减累加
do
load /=2
load += 1024 + 1024y + 1024y^2 +…+ 1024*y^LOAD_AVG_PERIOD
n -= period
while(n > LOAD_AVG_PERIOD) - 1024 + 1024y + 1024y^2 +…+ 1024*y^32=runnable_avg_yN_sum[32]
decay_load()只是计算y^n,而__contrib是计算一个对比队列的和:y + y^2 + y^3 … + y^n.计算方式如下:
runnable_avg_yN_sum[]数组是使用查表法来计算n=32位内的等比队列求和:
runnable_avg_yN_sum[1] = y^1 * 1024 = 0.978520621 * 1024 = 1002
runnable_avg_yN_sum[2] = (y^1 + y^2) * 1024 = 1982
…
runnable_avg_yN_sum[32] = (y^1 + y^2 … + y^32) * 1024 = 23371
实现代码和查表数据如下:
static u32 __compute_runnable_contrib(u64 n)
{
u32 contrib = 0;
if (likely(n <= LOAD_AVG_PERIOD))
return runnable_avg_yN_sum[n];
else if (unlikely(n >= LOAD_AVG_MAX_N))
return LOAD_AVG_MAX;
/* Compute Sum k^n combining precomputed values for k^i, Sum k^j */
do {
contrib /= 2; /* y^LOAD_AVG_PERIOD = 1/2 */
contrib += runnable_avg_yN_sum[LOAD_AVG_PERIOD];
n -= LOAD_AVG_PERIOD;
} while (n > LOAD_AVG_PERIOD);
contrib = decay_load(contrib, n);
return contrib + runnable_avg_yN_sum[n];
}
/*
* Precomputed Sum y^k { 1<=k<=n }. These are floor(true_value) to prevent
* over-estimates when re-combining.
*/
static const u32 runnable_avg_yN_sum[] = {
0, 1002, 1982, 2941, 3880, 4798, 5697, 6576, 7437, 8279, 9103,
9909,10698,11470,12226,12966,13690,14398,15091,15769,16433,17082,
17718,18340,18949,19545,20128,20698,21256,21802,22336,22859,23371,
};
针对__contrib第二点当period>345的时候,load变成一个常数怎么理解的?
即load = LOAD_AVG_MAX (47742),我们简单来证明以下:
设一个等比数列的首项是a1,公比是y,数列前n项和是Sn,当公比不为1时
Sn=a1+a1y+a1y2+…+a1y(n-1)
将这个式子两边同时乘以公比y,得
ySn=a1y+a1y2+…+a1y(n-1)+a1y^n
两式相减,得
(1-y)Sn=a1-a1y^n
所以,当公比不为1时,等比数列的求和公式:
Sn=a1(1-y^n)/(1-y)
对于一个无穷递降数列,数列的公比小于1,当上式得n趋向于正无穷大时,分子括号中的值趋近于1,取极限即得无穷递减数列求和公式:
S=a1/(1-y)
由于要使y^32 = 0.5, 那么经过计算之后,y≈0.9785 (0.9785^32≈0.498823)
所以对于period > LOAD_AVG_MAX_N(345),等比数列求和数值如下:
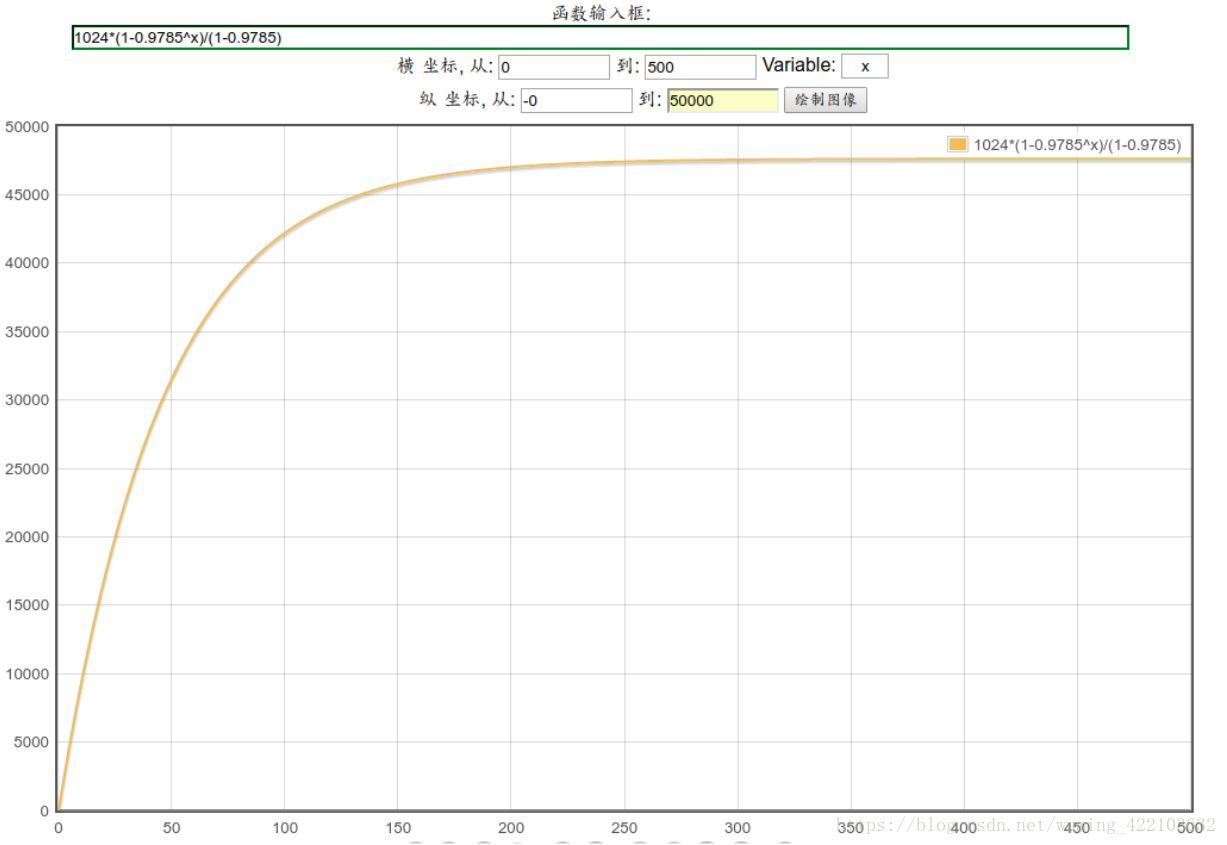
sn=a1(1-yn)/(1-y)=1024*(1-0.9785n)/(1-0.9785)
画出曲线图如下:
从当n趋于一个数值,当n增大,等比数列之后增加几乎可以忽略,并且无穷大∞,则等比数列之和为a1/(1-y)=1024/(1-0.9785)≈47627.9069988967,与47742数值差不多.
上面说明了原理,下面就是实际的代码分析了.
那么上面的两个表格runnable_avg_yN_inv和runnable_avg_yN_sum是怎么计算的,下面是一个通过C语言计算的小程序:
#include <stdio.h>
#include <math.h>
#if 1
#define N 32
#define WMULT_SHIFT 32
const long WMULT_CONST = ((1UL << N) - 1);
double y;
long runnable_avg_yN_inv[N];
void calc_mult_inv()
{
int i;
double yn = 0;
printf("inverses
");
for (i = 0; i < N; i++) {
yn = (double)WMULT_CONST * pow(y, i);
runnable_avg_yN_inv[i] = yn;
printf("%2d: 0x%8lx
", i, runnable_avg_yN_inv[i]);
}
printf("
");
}
long mult_inv(long c, int n)
{
return (c * runnable_avg_yN_inv[n]) >> WMULT_SHIFT;
}
void calc_yn_sum(int n)
{
int i;
double sum = 0, sum_fl = 0, diff = 0;
/*
* We take the floored sum to ensure the sum of partial sums is never
* larger than the actual sum.
*/
printf("sum y^n
");
printf(" %8s %8s %8s
", "exact", "floor", "error");
for (i = 1; i <= n; i++) {
sum = (y * sum + y * 1024);
sum_fl = floor(y * sum_fl+ y * 1024);
printf("%2d: %8.0f %8.0f %8.0f
", i, sum, sum_fl,
sum_fl - sum);
}
printf("
");
}
void calc_conv(long n)
{
long old_n;
int i = -1;
printf("convergence (LOAD_AVG_MAX, LOAD_AVG_MAX_N)
");
do {
old_n = n;
n = mult_inv(n, 1) + 1024;
i++;
} while (n != old_n);
printf("%d> %ld
", i - 1, n);
printf("
");
}
#endif
int main(void)
{
#if 1
/* y^32 = 0.5,so y=pow(0.5,32.0)*/
y = pow(0.5, 1/(double)N);
calc_mult_inv();
calc_conv(1024);
calc_yn_sum(N);
#endif
return 0;
}
runnable_avg_yN_inv[i]的数值如下:
0: 0xffffffff
1: 0xfa83b2da
2: 0xf5257d14
3: 0xefe4b99a
4: 0xeac0c6e6
5: 0xe5b906e6
6: 0xe0ccdeeb
7: 0xdbfbb796
8: 0xd744fcc9
9: 0xd2a81d91
10: 0xce248c14
11: 0xc9b9bd85
12: 0xc5672a10
13: 0xc12c4cc9
14: 0xbd08a39e
15: 0xb8fbaf46
16: 0xb504f333
17: 0xb123f581
18: 0xad583ee9
19: 0xa9a15ab4
20: 0xa5fed6a9
21: 0xa2704302
22: 0x9ef5325f
23: 0x9b8d39b9
24: 0x9837f050
25: 0x94f4efa8
26: 0x91c3d373
27: 0x8ea4398a
28: 0x8b95c1e3
29: 0x88980e80
30: 0x85aac367
31: 0x82cd8698
与table是吻合的.
也就是说两个table的通项公式如下(我们知道y^32约等于0.5推导出y=0.9785):
runnable_avg_yN_inv[n]=(2^32-1) * (0.9785^n);
runnable_avg_yN_sum[n]=1024(y + y2+…+yn);*
所以在函数decay_load的时候,需要>> 32,这是单个时间点的衰减数值
下面画一张图来详细说明上面的逻辑关系:
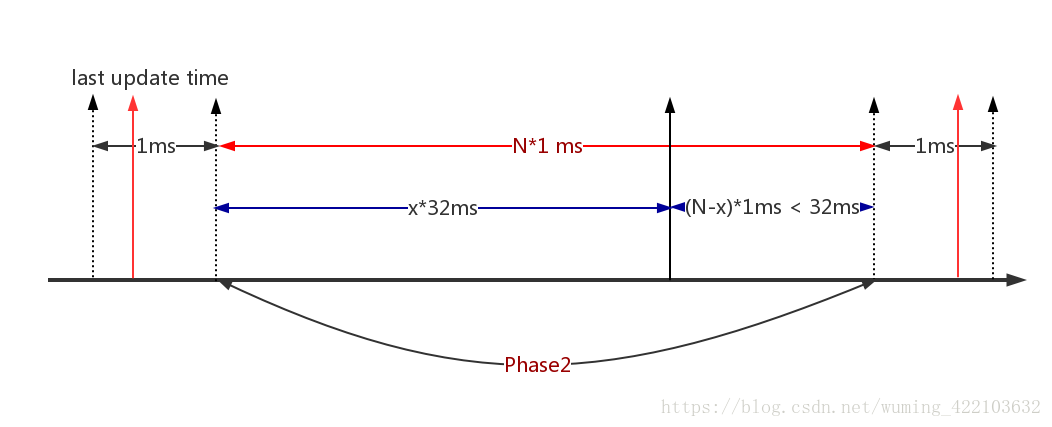
decay_load是计算Phase2的一个load的衰减,比如在Phase2起始阶段load为load_x,经过两个阶段的衰减:
- x*32ms=(N/32) * 32之后变为:load_x >> (N/32),即每隔32ms,load_x衰减一半,符合y^32=0.5.
- 那么剩下的(N-x)ms,继续衰减,使用公式计算即:(load_x >> (N/32)) * y^(N-x).这样就明白了.单个load的衰减计算方式.
对于累加load的计算方式也使用这张图来说明:
__compute_runnable_contrib(N)怎么来计算累加的负载:
- x*32ms=(N/32) * 32,可以根据查表计是32ms倍数的周期内,累加的负载可以通过查表获取,并且累加的负载在每个32ms周期都会衰减一半,23371=runnable_avg_yN_sum[31].即计算公式如下:
或者:
contrib = 1024(y+y2+…+y32+…+y^64…) = 1024(y+…+y32)+y32*1024(y+…+y32)…
由于y^32=0.5.所以可以对上
- 对前x*32ms已经累加了,现在需要对这部分在(N-x)进行衰减操作,即contrib=decay_load(contrib,N-x)
- 最后计算contrib+runnable_avg_yN_sum[N-x]就是最后累加的结果了.
###PELT Entity级的负载计算
- Entity级的负载计算也称作PELT(Per-Entity Load Tracking)。
- 注意负载计算时使用的时间都是实际运行时间而不是虚拟运行时间vruntime。
过程如下:
scheduler_tick() -> task_tick_fair() -> entity_tick() -> update_load_avg()
/* Update task and its cfs_rq load average */
static inline void update_load_avg(struct sched_entity *se, int flags)
{
struct cfs_rq *cfs_rq = cfs_rq_of(se);
u64 now = cfs_rq_clock_task(cfs_rq);
int cpu = cpu_of(rq_of(cfs_rq));
int decayed;
void *ptr = NULL;
/*
* Track task load average for carrying it to new CPU after migrated, and
* track group sched_entity load average for task_h_load calc in migration
*//*cfs load tracing时间已经update,也就是已经初始化过了
SKIP_AGE_LOAD是忽略load tracing的flag*/
if (se->avg.last_update_time && !(flags & SKIP_AGE_LOAD)) {
/*核心函数,即PELT的实现,注意se->on_rq的数值,如果一直在运行的进程,则
se->on_rq,load=老负载衰减+新负载,如果是休眠唤醒进程se->on_rq=0,则他们在
休眠期间的load不会累加,只有老负载被衰减,睡眠时间不会统计在内,直到task在rq里面*/
__update_load_avg(now, cpu, &se->avg,
se->on_rq * scale_load_down(se->load.weight),
cfs_rq->curr == se, NULL);
}
decayed = update_cfs_rq_load_avg(now, cfs_rq, true);
decayed |= propagate_entity_load_avg(se);
if (decayed && (flags & UPDATE_TG))
update_tg_load_avg(cfs_rq, 0);
if (entity_is_task(se)) {
#ifdef CONFIG_SCHED_WALT
ptr = (void *)&(task_of(se)->ravg);
#endif
trace_sched_load_avg_task(task_of(se), &se->avg, ptr);
}
}
#####核心函数1 __update_load_avg()的实现
我们先明白下面几个参数的含义:
- load_sum
- util_sum
- load_avg
- util_avg
上面几个涉及到cfs_rq结构体的成员变量:
struct cfs_rq {
..............
/*
* CFS load tracking
*/
struct sched_avg avg;
u64 runnable_load_sum;
unsigned long runnable_load_avg;
..............
}
/*
* The load_avg/util_avg accumulates an infinite geometric series.
* 1) load_avg factors frequency scaling into the amount of time that a
* sched_entity is runnable on a rq into its weight. For cfs_rq, it is the
* aggregated such weights of all runnable and blocked sched_entities.
* 2) util_avg factors frequency and cpu scaling into the amount of time
* that a sched_entity is running on a CPU, in the range [0..SCHED_LOAD_SCALE].
* For cfs_rq, it is the aggregated such times of all runnable and
* blocked sched_entities.
* The 64 bit load_sum can:
* 1) for cfs_rq, afford 4353082796 (=2^64/47742/88761) entities with
* the highest weight (=88761) always runnable, we should not overflow
* 2) for entity, support any load.weight always runnable
*/
struct sched_avg {
u64 last_update_time, load_sum;
u32 util_sum, period_contrib;
unsigned long load_avg, util_avg;
};
而且如果知道了load_sum,util_sum,runnable_load_sum,这几个数值除以LOAD_AVG_MAX(47742)则就可以直接计算load_avg,util_avg,runnable_load_avg,即:
util_avg = util_sum / LOAD_AVG_MAX(47742).
- scale_freq:https://blog.csdn.net/wukongmingjing/article/details/81635383
- scale_cpu:https://blog.csdn.net/wukongmingjing/article/details/81635383
关键函数的代码如下:
/*
* We can represent the historical contribution to runnable average as the
* coefficients of a geometric series. To do this we sub-divide our runnable
* history into segments of approximately 1ms (1024us); label the segment that
* occurred N-ms ago p_N, with p_0 corresponding to the current period, e.g.
*
* [<- 1024us ->|<- 1024us ->|<- 1024us ->| ...
* p0 p1 p2
* (now) (~1ms ago) (~2ms ago)
*
* Let u_i denote the fraction of p_i that the entity was runnable.
*
* We then designate the fractions u_i as our co-efficients, yielding the
* following representation of historical load:
* u_0 + u_1*y + u_2*y^2 + u_3*y^3 + ...
*
* We choose y based on the with of a reasonably scheduling period, fixing:
* y^32 = 0.5
*
* This means that the contribution to load ~32ms ago (u_32) will be weighted
* approximately half as much as the contribution to load within the last ms
* (u_0).
*
* When a period "rolls over" and we have new u_0`, multiplying the previous
* sum again by y is sufficient to update:
* load_avg = u_0` + y*(u_0 + u_1*y + u_2*y^2 + ... )
* = u_0 + u_1*y + u_2*y^2 + ... [re-labeling u_i --> u_{i+1}]
*/
static __always_inline int
__update_load_avg(u64 now, int cpu, struct sched_avg *sa,
unsigned long weight, int running, struct cfs_rq *cfs_rq)
{
u64 delta, scaled_delta, periods;
u32 contrib;
unsigned int delta_w, scaled_delta_w, decayed = 0;
unsigned long scale_freq, scale_cpu;
#ifdef CONFIG_64BIT_ONLY_CPU
struct sched_entity *se;
unsigned long load_avg_before = sa->load_avg;
#endif
/*就是示意图中的delta1+delta2+delta3*/
delta = now - sa->last_update_time;
/*
* This should only happen when time goes backwards, which it
* unfortunately does during sched clock init when we swap over to TSC.
*/
if ((s64)delta < 0) {
sa->last_update_time = now;
return 0;
}
/*
* Use 1024ns as the unit of measurement since it's a reasonable
* approximation of 1us and fast to compute.
*/
delta >>= 10;
if (!delta)
return 0;
sa->last_update_time = now;
/*scale_freq = (curr_freq << 10)/policy->max*/
scale_freq = arch_scale_freq_capacity(NULL, cpu);
/*scale_cpu = capacity[cpu],dts获取的,不同cluster capacity不同*/
scale_cpu = arch_scale_cpu_capacity(NULL, cpu);
trace_sched_contrib_scale_f(cpu, scale_freq, scale_cpu);
/* delta_w is the amount already accumulated against our next period */
delta_w = sa->period_contrib;
/*表示delta1+delta2大于一个最小刻度1024,如果小于,则就只剩下delta3计算,delta1,
delta2不存在*/
if (delta + delta_w >= 1024) {
decayed = 1;
/* how much left for next period will start over, we don't know yet */
sa->period_contrib = 0;
/*
* Now that we know we're crossing a period boundary, figure
* out how much from delta we need to complete the current
* period and accrue it.
*/
/*开始Phase1阶段的load_sum 和util_sum的计算*/
delta_w = 1024 - delta_w;
scaled_delta_w = cap_scale(delta_w, scale_freq);
if (weight) {
sa->load_sum += weight * scaled_delta_w;
if (cfs_rq) {
cfs_rq->runnable_load_sum +=
weight * scaled_delta_w;
}
}
if (running)
sa->util_sum += scaled_delta_w * scale_cpu;
/*结束Phase1阶段的load_sum 和util_sum的计算*/
delta -= delta_w;
/* Figure out how many additional periods this update spans */
/*开始Phase2阶段的load_sum 和util_sum的计算,计算阶段Phase2存在多少个1024
的倍数和余数*/
periods = delta / 1024;
delta %= 1024;
/*对阶段Phase1的load_sum进行衰减*/
sa->load_sum = decay_load(sa->load_sum, periods + 1);
if (cfs_rq) {
/*对阶段Phase1的runnable_load_sum进行衰减*/
cfs_rq->runnable_load_sum =
decay_load(cfs_rq->runnable_load_sum, periods + 1);
}
/*对Phase1阶段util_sum进行衰减*/
sa->util_sum = decay_load((u64)(sa->util_sum), periods + 1);
/*至此,上面已经得到了阶段Phase2衰减前的load_sum,util_sum,
runnable_load_sum的数值*/
/* Efficiently calculate sum (1..n_period) 1024*y^i */
/*对Phase2的load/util数据进行衰减*/
contrib = __compute_runnable_contrib(periods);
contrib = cap_scale(contrib, scale_freq);
if (weight) {
sa->load_sum += weight * contrib;
if (cfs_rq)
cfs_rq->runnable_load_sum += weight * contrib;
}
if (running)
sa->util_sum += contrib * scale_cpu;
}
/*结束Phase2阶段的load_sum 和util_sum的计算*/
/* Remainder of delta accrued against u_0` */
/*开始阶段Phase3的的load/util的计算*/
scaled_delta = cap_scale(delta, scale_freq);
if (weight) {
sa->load_sum += weight * scaled_delta;
if (cfs_rq)
cfs_rq->runnable_load_sum += weight * scaled_delta;
}
if (running)
sa->util_sum += scaled_delta * scale_cpu;
/*结束阶段Phase3的的load/util的计算*/
/*sa->period_contrib ∈[0,1024)*/
sa->period_contrib += delta;
/*如果衰减了,则计算load的avg的数值,否则由于颗粒度太小,没有计算的必要*/
if (decayed) {
sa->load_avg = div_u64(sa->load_sum, LOAD_AVG_MAX);
if (cfs_rq) {
cfs_rq->runnable_load_avg =
div_u64(cfs_rq->runnable_load_sum, LOAD_AVG_MAX);
}
sa->util_avg = sa->util_sum / LOAD_AVG_MAX;
}
#ifdef CONFIG_64BIT_ONLY_CPU
if (!cfs_rq) {
if (is_sched_avg_32bit(sa)) {
se = container_of(sa, struct sched_entity, avg);
cfs_rq_of(se)->runnable_load_avg_32bit +=
sa->load_avg - load_avg_before;
}
}
#endif
return decayed;
}
/*
* Approximate:
* val * y^n, where y^32 ~= 0.5 (~1 scheduling period)
*/
static __always_inline u64 decay_load(u64 val, u64 n)
{
unsigned int local_n;
if (!n)
return val;
else if (unlikely(n > LOAD_AVG_PERIOD * 63))
return 0;
/* after bounds checking we can collapse to 32-bit */
local_n = n;
/*计算公式为:load = (load >> (n/period)) * y^(n%period),如果n是32的整数倍
,因为2^32 = 1/2,相当于右移一位计算n有多少个32,每个32右移一位*/
/*
* As y^PERIOD = 1/2, we can combine
* y^n = 1/2^(n/PERIOD) * y^(n%PERIOD)
* With a look-up table which covers y^n (n<PERIOD)
*
* To achieve constant time decay_load.
*/
if (unlikely(local_n >= LOAD_AVG_PERIOD)) {
val >>= local_n / LOAD_AVG_PERIOD;
local_n %= LOAD_AVG_PERIOD;
}
/*将val*y^32,转化为val*runnable_avg_yN_inv[n%LOAD_AVG_PERIOD]>>32*/
val = mul_u64_u32_shr(val, runnable_avg_yN_inv[local_n], 32);
return val;
}
/*
* For updates fully spanning n periods, the contribution to runnable
* average will be: Sum 1024*y^n
*
* We can compute this reasonably efficiently by combining:
* y^PERIOD = 1/2 with precomputed Sum 1024*y^n {for n <PERIOD}
*/
static u32 __compute_runnable_contrib(u64 n)
{
u32 contrib = 0;
if (likely(n <= LOAD_AVG_PERIOD))
return runnable_avg_yN_sum[n];
else if (unlikely(n >= LOAD_AVG_MAX_N))
return LOAD_AVG_MAX;
/*如果n>32,计算32的整数部分*/
/* Compute Sum k^n combining precomputed values for k^i, Sum k^j */
do {
/*每整数32的衰减就是0.5*/
contrib /= 2; /* y^LOAD_AVG_PERIOD = 1/2 */
contrib += runnable_avg_yN_sum[LOAD_AVG_PERIOD];
n -= LOAD_AVG_PERIOD;
} while (n > LOAD_AVG_PERIOD);
/*将整数部分对余数n进行衰减*/
contrib = decay_load(contrib, n);
/*剩余余数n,使用查表法计算*/
return contrib + runnable_avg_yN_sum[n];
}
#####核心函数2 update_cfs_rq_load_avg()的实现
/**
* update_cfs_rq_load_avg - update the cfs_rq's load/util averages
* @now: current time, as per cfs_rq_clock_task()
* @cfs_rq: cfs_rq to update
* @update_freq: should we call cfs_rq_util_change() or will the call do so
*
* The cfs_rq avg is the direct sum of all its entities (blocked and runnable)
* avg. The immediate corollary is that all (fair) tasks must be attached, see
* post_init_entity_util_avg().
*
* cfs_rq->avg is used for task_h_load() and update_cfs_share() for example.
*
* Returns true if the load decayed or we removed load.
*
* Since both these conditions indicate a changed cfs_rq->avg.load we should
* call update_tg_load_avg() when this function returns true.
*/
static inline int
update_cfs_rq_load_avg(u64 now, struct cfs_rq *cfs_rq, bool update_freq)
{
struct sched_avg *sa = &cfs_rq->avg;
int decayed, removed = 0, removed_util = 0;
/*是否设置了remove_load_avg和remove_util_avg,如果设置了就修正之前计算的
load/util数值*/
if (atomic_long_read(&cfs_rq->removed_load_avg)) {
s64 r = atomic_long_xchg(&cfs_rq->removed_load_avg, 0);
sub_positive(&sa->load_avg, r);
sub_positive(&sa->load_sum, r * LOAD_AVG_MAX);
removed = 1;
set_tg_cfs_propagate(cfs_rq);
}
if (atomic_long_read(&cfs_rq->removed_util_avg)) {
long r = atomic_long_xchg(&cfs_rq->removed_util_avg, 0);
sub_positive(&sa->util_avg, r);
sub_positive(&sa->util_sum, r * LOAD_AVG_MAX);
removed_util = 1;
set_tg_cfs_propagate(cfs_rq);
}
/*对校准后的load进行重新计算*/
decayed = __update_load_avg(now, cpu_of(rq_of(cfs_rq)), sa,
scale_load_down(cfs_rq->load.weight), cfs_rq->curr != NULL, cfs_rq);
#ifndef CONFIG_64BIT
smp_wmb();
cfs_rq->load_last_update_time_copy = sa->last_update_time;
#endif
/* Trace CPU load, unless cfs_rq belongs to a non-root task_group */
if (cfs_rq == &rq_of(cfs_rq)->cfs)
trace_sched_load_avg_cpu(cpu_of(rq_of(cfs_rq)), cfs_rq);
/*如果为true,则调用schedutil governor进行频率的调整!!!*/
if (update_freq)
cfs_rq_util_change(cfs_rq);
return decayed || removed;
}
update_load_avg剩下的函数执行如下:
- propagate_entity_load_avg,更新调度实体本身自己的load/util信息.如果是一个进程则不需要propagate处理.
- 根据decayed的数值和需要更新进程组信息,则调用update_tg_load_avg,更新task_group信息
###CPU级的负载计算update_cpu_load_active(rq)
__update_load_avg()是计算se/cfs_rq级别的负载,在cpu级别linux使用update_cpu_load_active(rq)来计算整个cpu->rq负载的变化趋势。计算也是周期性的,周期为TICK(时间不固定,由于是tickless系统)。
scheduler_tick()----->
/*
* Called from scheduler_tick()
*/
void update_cpu_load_active(struct rq *this_rq)
{ /*获取cfs_rq的runnable_load_avg的数值*/
unsigned long load = weighted_cpuload(cpu_of(this_rq));
/*
* See the mess around update_idle_cpu_load() / update_cpu_load_nohz().
*/ /*设置更新rq load的时间戳*/
this_rq->last_load_update_tick = jiffies;
/核心函数*/
__update_cpu_load(this_rq, load, 1);
}
/* Used instead of source_load when we know the type == 0 */
static unsigned long weighted_cpuload(const int cpu)
{
return cfs_rq_runnable_load_avg(&cpu_rq(cpu)->cfs);
}
static inline unsigned long cfs_rq_runnable_load_avg(struct cfs_rq *cfs_rq)
{
/*这个数值在setity级别的计算过程中已经update了*/
return cfs_rq->runnable_load_avg;
}
/*
* Update rq->cpu_load[] statistics. This function is usually called every
* scheduler tick (TICK_NSEC). With tickless idle this will not be called
* every tick. We fix it up based on jiffies.
*/
static void __update_cpu_load(struct rq *this_rq, unsigned long this_load,
unsigned long pending_updates)
{
int i, scale;
/*统计数据使用*/
this_rq->nr_load_updates++;
/* Update our load: */
/*将当前最新的load,更新在cpu_load[0]中*/
this_rq->cpu_load[0] = this_load; /* Fasttrack for idx 0 */
for (i = 1, scale = 2; i < CPU_LOAD_IDX_MAX; i++, scale += scale) {
unsigned long old_load, new_load;
/* scale is effectively 1 << i now, and >> i divides by scale */
old_load = this_rq->cpu_load[i];
/*对old_load进行衰减.果因为进入noHZ模式,有pending_updates个tick没有
更新,先老化原有负载*/
old_load = decay_load_missed(old_load, pending_updates - 1, i);
new_load = this_load;
/*
* Round up the averaging division if load is increasing. This
* prevents us from getting stuck on 9 if the load is 10, for
* example.
*/
if (new_load > old_load)
new_load += scale - 1;
/*cpu_load的计算公式 */
this_rq->cpu_load[i] = (old_load * (scale - 1) + new_load) >> i;
}
/*更新rq的age_stamp时间戳,即rq从cpu启动到现在存在的时间(包括idle和running时间)
,同时更新rq里面rt_avg负载,即每个周期(500ms)衰减一半*/
sched_avg_update(this_rq);
}
void sched_avg_update(struct rq *rq)
{
s64 period = sched_avg_period();
while ((s64)(rq_clock(rq) - rq->age_stamp) > period) {
/*
* Inline assembly required to prevent the compiler
* optimising this loop into a divmod call.
* See __iter_div_u64_rem() for another example of this.
*/
asm("" : "+rm" (rq->age_stamp));
rq->age_stamp += period;
rq->rt_avg /= 2;
}
}
代码注释中详细解释了cpu_load的计算方法:
- 每个tick计算不同idx时间等级的load,计算公式:load = (2^idx - 1) / 2^idx * load + 1 / 2^idx * cur_load
- 如果cpu因为noHZ错过了(n-1)个tick的更新,那么计算load要分两步:
- 首先老化(decay)原有的load:load = ((2^idx - 1) / 2idx)(n-1) * load
- 再按照一般公式计算load:load = load = (2^idx - 1) / 2^idx) * load + 1 / 2^idx * cur_load
- 为了decay的加速计算,设计了decay_load_missed()查表法计算:
/*
* The exact cpuload at various idx values, calculated at every tick would be
* load = (2^idx - 1) / 2^idx * load + 1 / 2^idx * cur_load
*
* If a cpu misses updates for n-1 ticks (as it was idle) and update gets called
* on nth tick when cpu may be busy, then we have:
* load = ((2^idx - 1) / 2^idx)^(n-1) * load
* load = (2^idx - 1) / 2^idx) * load + 1 / 2^idx * cur_load
*
* decay_load_missed() below does efficient calculation of
* load = ((2^idx - 1) / 2^idx)^(n-1) * load
* avoiding 0..n-1 loop doing load = ((2^idx - 1) / 2^idx) * load
*
* The calculation is approximated on a 128 point scale.
* degrade_zero_ticks is the number of ticks after which load at any
* particular idx is approximated to be zero.
* degrade_factor is a precomputed table, a row for each load idx.
* Each column corresponds to degradation factor for a power of two ticks,
* based on 128 point scale.
* Example:
* row 2, col 3 (=12) says that the degradation at load idx 2 after
* 8 ticks is 12/128 (which is an approximation of exact factor 3^8/4^8).
*
* With this power of 2 load factors, we can degrade the load n times
* by looking at 1 bits in n and doing as many mult/shift instead of
* n mult/shifts needed by the exact degradation.
*/
#define DEGRADE_SHIFT 7
static const unsigned char
degrade_zero_ticks[CPU_LOAD_IDX_MAX] = {0, 8, 32, 64, 128};
static const unsigned char
degrade_factor[CPU_LOAD_IDX_MAX][DEGRADE_SHIFT + 1] = {
{0, 0, 0, 0, 0, 0, 0, 0},
{64, 32, 8, 0, 0, 0, 0, 0},
{96, 72, 40, 12, 1, 0, 0},
{112, 98, 75, 43, 15, 1, 0},
{120, 112, 98, 76, 45, 16, 2} };
/*
* Update cpu_load for any missed ticks, due to tickless idle. The backlog
* would be when CPU is idle and so we just decay the old load without
* adding any new load.
*/
static unsigned long
decay_load_missed(unsigned long load, unsigned long missed_updates, int idx)
{
int j = 0;
if (!missed_updates)
return load;
if (missed_updates >= degrade_zero_ticks[idx])
return 0;
if (idx == 1)
return load >> missed_updates;
while (missed_updates) {
if (missed_updates % 2)
load = (load * degrade_factor[idx][j]) >> DEGRADE_SHIFT;
missed_updates >>= 1;
j++;
}
return load;
}
- cpu_load[]含5条均线,反应不同时间窗口长度下的负载情况;主要供load_balance()在不同场景判断是否负载平衡的比较基准,常用为cpu_load[0]和cpu_load[1];
- cpu_load[index]对应的时间长度为{0, 8, 32, 64, 128},单位为tick;
- 移动均线的目的在于平滑样本的抖动,确定趋势的变化方向;
###系统级的负载计算calc_global_load_tick()
系统级的平均负载(load average)可以通过以下命令(uptime、top、cat /proc/loadavg)查看:
mate20:/ # cat proc/loadavg && uptime
1.38 1.49 1.58 1/1085 20184
16:10:43 up 1 day, 2:29, 0 users, load average: 1.38, 1.49, 1.58
“load average:”后面的3个数字分别表示1分钟、5分钟、15分钟的load average。可以从几方面去解析load average:
- If the averages are 0.0, then your system is idle.
- If the 1 minute average is higher than the 5 or 15 minute averages, then load is increasing.
- If the 1 minute average is lower than the 5 or 15 minute averages, then load is decreasing.
- If they are higher than your CPU count, then you might have a performance problem (it depends).
最早的系统级平均负载(load average)只会统计runnable状态。但是linux后面觉得这种统计方式代表不了系统的真实负载;举一个例子:系统换一个低速硬盘后,他的 runnable负载还会小于高速硬盘时的值;linux认为睡眠状态 (TASK_INTERRUPTIBLE/TASK_UNINTERRUPTIBLE)也是系统的一种负载,系统得不到服务是因为io/外设的负载过重; 系统级负载统计函数calc_global_load_tick()中会把 (this_rq->nr_running+this_rq->nr_uninterruptible)都计入负载.
下面来看看具体的代码计算:
每个cpu每隔5s更新本cpu rq的(nr_running+nr_uninterruptible)任务数量到系统全局变量 calc_load_tasks,calc_load_tasks是整系统多个cpu(nr_running+nr_uninterruptible)任 务数量的总和,多cpu在访问calc_load_tasks变量时使用原子操作来互斥。
/*
* Called from scheduler_tick() to periodically update this CPU's
* active count.
*/
void calc_global_load_tick(struct rq *this_rq)
{
long delta;
/*判断5s更新周期是否到达*/
if (time_before(jiffies, this_rq->calc_load_update))
return;
/*计算本cpu的负载变化到全局变量calc_load_tasks中*/
delta = calc_load_fold_active(this_rq);
if (delta)
atomic_long_add(delta, &calc_load_tasks);
/*更新calc_load_update时间.LOAD_FREQ:(5*HZ+1),5s*/
this_rq->calc_load_update += LOAD_FREQ;
}
多个cpu更新calc_load_tasks,但是计算load只由一个cpu来完成,这个cpu就是tick_do_timer_cpu。在 linux time一文中,我们看到这个cpu就是专门来更新时间戳timer的(update_wall_time())。实际上它在更新时间戳的同时也会调用 do_timer() -> calc_global_load()来计算系统负载。
核心算法calc_load()的思想也是:旧的load老化系数 + 新load系数
假设单位1为FIXED_1=2^11=2028,EXP_1=1884、EXP_5=2014、EXP_15=2037,load的计算:
load = old_load(EXP_?/FIXED_1) + new_load(FIXED_1-EXP_?)/FIXED_1**
do_timer() -> calc_global_load()
↓
void calc_global_load(unsigned long ticks)
{
long active, delta;
/* (1) 计算的间隔时间为5s + 10tick,
加10tick的目的就是让所有cpu都更新完calc_load_tasks,
tick_do_timer_cpu再来计算
*/
if (time_before(jiffies, calc_load_update + 10))
return;
/*
* Fold the 'old' idle-delta to include all NO_HZ cpus.
*/
delta = calc_load_fold_idle();
if (delta)
atomic_long_add(delta, &calc_load_tasks);
/* (2) 读取全局统计变量 */
active = atomic_long_read(&calc_load_tasks);
active = active > 0 ? active * FIXED_1 : 0;
/* (3) 计算1分钟、5分钟、15分钟的负载 */
avenrun[0] = calc_load(avenrun[0], EXP_1, active);
avenrun[1] = calc_load(avenrun[1], EXP_5, active);
avenrun[2] = calc_load(avenrun[2], EXP_15, active);
calc_load_update += LOAD_FREQ;
/*
* In case we idled for multiple LOAD_FREQ intervals,
catch up in bulk. */
calc_global_nohz();
}
|→
/*
* a1 = a0 * e + a * (1 - e)
*/
static unsigned long
calc_load(unsigned long load, unsigned long exp, unsigned long active)
{
unsigned long newload;
newload = load * exp + active * (FIXED_1 - exp);
if (active >= load)
newload += FIXED_1-1;
return newload / FIXED_1;
}
#define FSHIFT 11 /* nr of bits of precision */
#define FIXED_1 (1<<FSHIFT) /* 1.0 as fixed-point */
#define LOAD_FREQ (5*HZ+1) /* 5 sec intervals */
#define EXP_1 1884 /* 1/exp(5sec/1min) as fixed-point */
#define EXP_5 2014 /* 1/exp(5sec/5min) */
#define EXP_15 2037 /* 1/exp(5sec/15min) */
对于cat /proc/loadavg的数值计算源码如下:
#define LOAD_INT(x) ((x) >> FSHIFT)
#define LOAD_FRAC(x) LOAD_INT(((x) & (FIXED_1-1)) * 100)
static int loadavg_proc_show(struct seq_file *m, void *v)
{
unsigned long avnrun[3];
get_avenrun(avnrun, FIXED_1/200, 0);
/*其实还是直接获取系统全局变量,avnrun的数值在计算系统负载的时候已经计算了*/
seq_printf(m, "%lu.%02lu %lu.%02lu %lu.%02lu %ld/%d %d
",
LOAD_INT(avnrun[0]), LOAD_FRAC(avnrun[0]),
LOAD_INT(avnrun[1]), LOAD_FRAC(avnrun[1]),
LOAD_INT(avnrun[2]), LOAD_FRAC(avnrun[2]),
nr_running(), nr_threads,
task_active_pid_ns(current)->last_pid);
return 0;
}
static int loadavg_proc_open(struct inode *inode, struct file *file)
{
return single_open(file, loadavg_proc_show, NULL);
}
static const struct file_operations loadavg_proc_fops = {
.open = loadavg_proc_open,
.read = seq_read,
.llseek = seq_lseek,
.release = single_release,
};
static int __init proc_loadavg_init(void)
{
proc_create("loadavg", 0, NULL, &loadavg_proc_fops);
return 0;
}
fs_initcall(proc_loadavg_init);
至此就计算完毕了.