算法导论 之 红黑树

转自：https://blog.csdn.net/qifengzou/article/details/17608863

• 作者：邹祁峰
• 邮箱：Qifeng.zou.job@hotmail.com
• 博客：http://blog.csdn.net/qifengzou
• 日期：2014.01.18 01:21
• 转载请注明来自"祁峰"的CSDN博客

1 引言

    在《算法导论 之 红黑树 - 插入》中已经对红黑树的5个性质做了较详细的分析，同时也给出了insert操作的C语言实现。首先我们再回顾一下红黑树的5个性质：

    ①、每个节点要么是红色的，要么是黑色的；

    ②、根结点是黑色的；

    ③、所有叶子结点（NIL）都是黑色的；

    ④、如果一个结点是红色，则它的两个儿子都是黑色的；

    ⑤、对任何一个结点，从该结点通过其子孙结点到达叶子结点（NIL）的所有路径上包含相同数目的黑结点。

   和插入操作一样，结点的删除操作的时间复杂度也是O（log2@N）[注：以2为底数，N为对数]，但删除操作的处理更复杂一些。

 

2 删除处理

2.1 外部接口

    调用接口删除指定key结点时，其内部首先会查找红黑树中是否存在key结点。如果key结点不存在，则无需进行任何的处理；如果key结点存在，则调用_rbt_delete()删除结点。

    红黑树是查找树的一种，其查找key结点的过程与查找树的查找过程极其相似。故，外部接口的实现代码如下：[注：代码中出现的数据类型、宏、枚举或函数定义可以参考《算法导论 之 红黑树 - 插入》]

1. /******************************************************************************
2. **函数名称: rbt_delete
3. **功 能: 删除结点(外部接口)
4. **输入参数:
5. ** tree: 红黑树
6. ** key: 关键字
7. **输出参数: NONE
8. **返 回: RBT_SUCCESS:成功 RBT_FAILED:失败
9. **实现描述:
10. ** 1. 如果key的结点不存在，则无需进行任何的处理；
11. ** 2. 如果key的结点存在，则调用_rbt_delete()删除结点。
12. **注意事项:
13. **作 者: # Qifeng.zou # 2013.12.27 #
14. ******************************************************************************/
15. int rbt_delete(rbt_tree_t *tree, int key)
16. {
17. rbt_node_t *node = tree->root;
18.  
19.  
20. while(tree->sentinel != node) {
21. if(key == node->key) {
22. return _rb_delete(tree, node); /* 找到：执行删除处理 */
23. } else if(key < node->key) {
24. node = node->lchild;
25. } else {
26. node = node->rchild;
27. }
28. }
29.  
30. return RBT_SUCCESS; /* 未找到 */
31. }

代码1 删除操作

2.2 删除过程

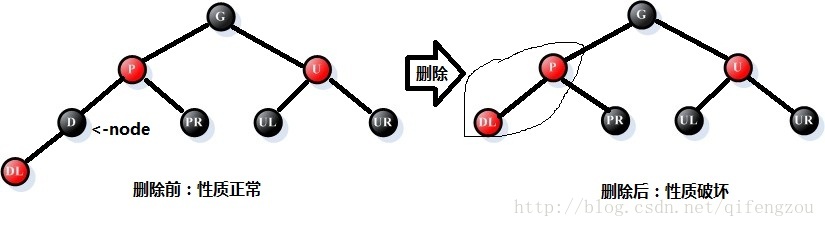
    假如需要删除结点D，则删除操作的过程有如下几种情况：[注：在以下所有绘制的红黑树中，均未绘制叶子结点]

情况1：被删结点D的左孩子为叶子结点，右孩子无限制（可为叶子结点，也可为非叶子结点）

    处理过程：

        ①、删除结点D，并用右孩子结点替代结点D的位置；

        ②、如果被删结点D为红色，则红黑树性质未被破坏，因此无需做其他调整；

        ③、如果被删结点D为黑色，则需进一步做调整处理。

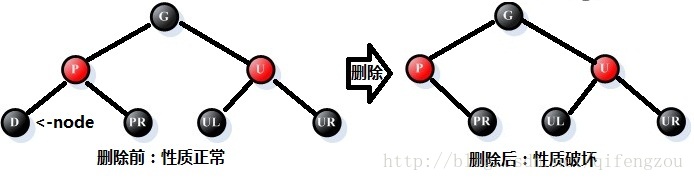
图1 情况1-1：左右孩子均为叶子结点

[叶子结点取代了结点D的位置]

 

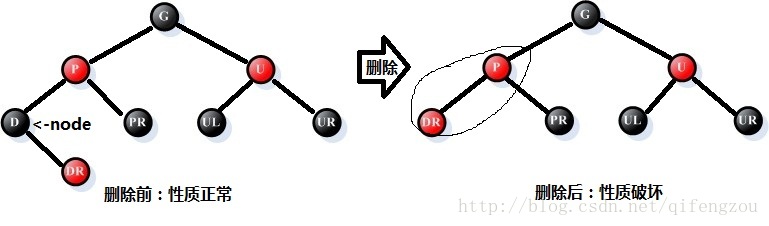
图2 情况1-2：左孩子为叶子结点 右孩子不为叶子结点

[结点DR取代了叶子结点的位置]

情况2: 被删结点D的右孩子为叶子结点，左孩子不为叶子结点

    处理过程：

        ①、删除结点D，并用左孩子节点替代结点D的位置；

        ②、如果被删结点D为红色，则红黑树性质未被破坏，因此不需做其他调整；

        ③、如果被删结点D为黑色，则需进一步做调整处理。

图3 情况2：右孩子为叶子结点 左孩子不为叶子结点

[结点DL取代结点D的位置]

情况3: 被删结点D的左右孩子均不为叶子节点

    处理过程：

        ①、找到结点D的后继结点S

        ②、将结点S的key值赋给结点D；

        ③、再将结点S从树中删除，并用结点S的右孩子替代结点S的位置；[注：从前面的描述可以看出，其实被删的是结点D的后继结点S]

        ④、如果被删结点S为红色，则红黑树性质未被破坏，因此不需做其他调整；

        ⑤、如果被删结点S为黑色，则需进一步做调整处理。

图4 情况3：左右孩子均不为叶子结点

[后继结点的右孩子SR取代后继结点S的位置]

    综合情况1、2、3可知，当实际被删的结点为黑色时，才需进一步做调整处理 —— 实际被删的结点为红色时，并不会破坏红黑树的5点性质，其实现的过程如下：[注：代码中出现的数据类型、宏、枚举或函数定义可以参考《算法导论 之 红黑树 - 插入》]

1. /******************************************************************************
2. **函数名称: _rbt_delete
3. **功 能: 删除结点(内部接口)
4. **输入参数:
5. ** tree: 红黑树
6. ** dnode: 将被删除的结点
7. **输出参数: NONE
8. **返 回: RBT_SUCCESS:成功 RBT_FAILED:失败
9. **实现描述:
10. ** 1. 如果将被删除的结点dnode无后继结点，则直接被删除，并被其左孩子或右孩子替代其位置
11. ** 2. 如果将被删除的结点dnode有后继结点，则将后继结点的其赋给dnode，并删除后继结点，
12. ** 再将后继结点的右孩子取代后继结点的位置
13. ** 3. 完成1、2的处理之后，如果红黑树的性质被破坏，则调用rbt_delete_fixup()进行调整
14. **注意事项:
15. **作 者: # Qifeng.zou # 2013.12.28 #
16. ******************************************************************************/
17. int _rb_delete(rbt_tree_t *tree, rbt_node_t *dnode)
18. {
19. rbt_node_t *parent = NULL, *next = NULL, *refer = NULL;
20.  
21.  
22. /* Case 1: 被删结点D的左孩子为叶子结点, 右孩子无限制(可为叶子结点，也可为非叶子结点) */
23. if(tree->sentinel == dnode->lchild) {
24. parent = dnode->parent;
25. refer = dnode->rchild;
26.  
27. refer->parent = parent;
28. if(tree->sentinel == parent) {
29. tree->root = refer;
30. } else if(dnode == parent->lchild) {
31. parent->lchild = refer;
32. } else { /* dnode == parent->rchild */
33. parent->rchild = refer;
34. }
35.  
36. if(rbt_is_red(dnode)) {
37. free(dnode);
38. return RBT_SUCCESS;
39. }
40.  
41. free(dnode);
42. return rbt_delete_fixup(tree, refer);
43. }
44. /* Case 2: 被删结点D的右孩子为叶子结点, 左孩子不为叶子结点 */
45. else if(tree->sentinel == dnode->rchild) {
46. parent = dnode->parent;
47. refer = dnode->lchild;
48.  
49. refer->parent = parent;
50. if(tree->sentinel == parent) {
51. tree->root = refer;
52. } else if(dnode == parent->lchild) {
53. parent->lchild = refer;
54. } else { /* dnode == parent->rchild */
55. parent->rchild = refer;
56. }
57.  
58. if(rbt_is_red(dnode)) {
59. free(dnode);
60. return RBT_SUCCESS;
61. }
62.  
63. free(dnode);
64. return rbt_delete_fixup(tree, refer);
65. }
66.  
67. /* Case 3: 被删结点D的左右孩子均不为叶子节点 */
68. /* 查找dnode的后继结点next */
69. next = dnode->rchild;
70. while(tree->sentinel != next->lchild) {
71. next = next->lchild;
72. }
73.  
74. parent = next->parent;
75. refer = next->rchild;
76.  
77. refer->parent = parent;
78. if(next == parent->lchild) {
79. parent->lchild = refer;
80. } else { /* next == parent->rchild */
81. parent->rchild = refer;
82. }
83.  
84. dnode->key = next->key;
85.  
86. if(rbt_is_red(next)) { /* Not black */
87. free(next);
88. return RBT_SUCCESS;
89. }
90.  
91. free(next);
92.  
93. return rbt_delete_fixup(tree, refer);
94. }

代码 2 删除结点

2.3 调整过程

    当红黑树中实际被删除的结点为黑色时，则可能破坏红黑树的5个性质。经过分析总结，破坏红黑树性质的情况有如下几种：

 

============================================================================

|| 前提1：参照结点N为父结点P的左孩子

============================================================================

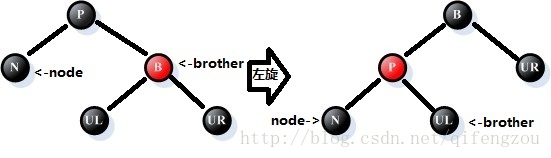
情况1：参照结点N的兄弟B是红色的

    处理过程：

        ①、将父结点P的颜色改为红色，兄弟结点的颜色改为黑色；

        ②、以父结点P为支点进行左旋处理；

        ③、情况1转变为情况2或3、4，后续需要依次判断处理。

    如下图所示：[注意：请注意图中处理前后node、brother指针的变化，这将是后续处理的参照]

图5 调整情况1

情况2：参照结点N的兄弟B是黑色的，且B的两个孩子都是黑色的

    处理过程：

        ①、将兄弟结点B的颜色改为红色

        ②、情况2处理完成后，不必再进行情况3、4的判断，但需重新循环判断前提1、2。

    如下图所示：[注意：请注意图中处理前后node、brother指针的变化，这将是后续处理的参照]

图6 调整情况2

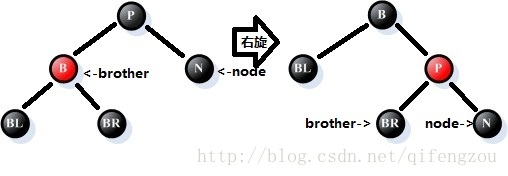
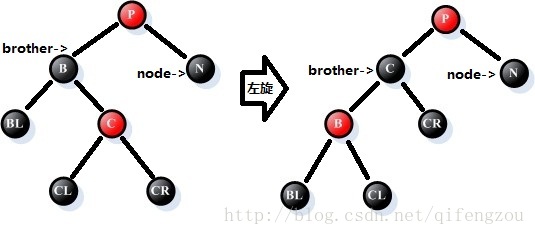
情况3：参照结点N的兄弟B是黑色的，且B的左孩子是红色的，右孩子是黑色的

    处理过程：

        ①、将兄弟结点B的颜色改为红色，结点B的左孩子改为黑色；

        ②、以结点B为支点进行右旋处理；

        ③、情况3转化为情况4，后续必须进行情况4的处理。

    如下图所示：[注意：请注意图中处理前后node、brother指针的变化，这将是后续处理的参照]

图7 调整情况3

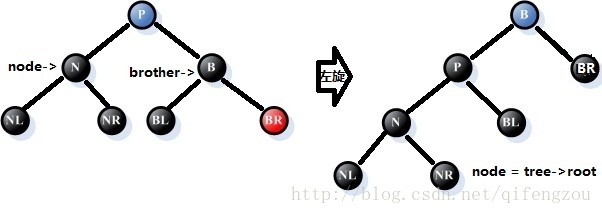
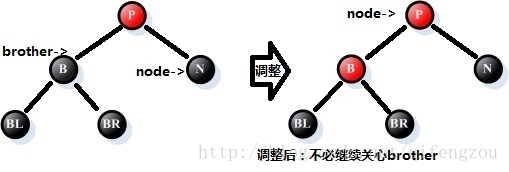
情况4：参照结点N的兄弟B是黑色的，且B的左孩子是黑色的，右孩子是红色的

    处理过程：

        ①、将父结点P的颜色拷贝给兄弟结点B，再将父结点P和兄弟结点的右孩子BR的颜色改为黑色；

        ②、以父结点P为支点，进行左旋处理；

        ③、将node改为树的根结点，也意味着调整结束。

    如下图所示：[注意：请注意图中处理前后node指针的变化，这将是后续处理的参照]

图8 调整情况4

[注：蓝色表示结点颜色可能为红，也可能为黑，在此也更能突出复制结点P的颜色给结点B]

============================================================================

 

 

|| 前提2：参照结点N为父结点P的右孩子

============================================================================

情况5：参照结点N的兄弟B是红色的

    处理过程：

        ①、将父结点P的颜色改为红色，兄弟结点的颜色改为黑色；

        ②、以父结点P为支点进行右旋处理；

        ③、情况5转变为情况6或7、8，后续需要依次判断处理。

    如下图所示：[注意：请注意图中处理前后node、brother指针的变化，这将是后续处理的参照]

图9 调整情况5

情况6：参照结点N的兄弟B是黑色的，且B的两个孩子都是黑色的

    处理过程：

        ①、将兄弟结点B的颜色改为红色；

        ②、情况6处理完成后，不必再进行情况7、8的判断，但需要重新循环判断前提1、2。

    如下图所示：[注意：请注意图中处理前后node、brother指针的变化，这将是后续处理的参照]

图10 调整情况6

情况7：参照结点N的兄弟B是黑色的，且B的右孩子是红色的，左孩子是黑色的

    处理过程：

        ①、将兄弟结点B的颜色改为红色，结点B的右孩子改为黑色；

        ②、以结点B为支点进行左旋处理；

        ③、情况7转化为情况8，后续必须进行情况8的处理。

    如下图所示：[注意：请注意图中处理前后node、brother指针的变化，这将是后续处理的参照]

图11 调整情况7

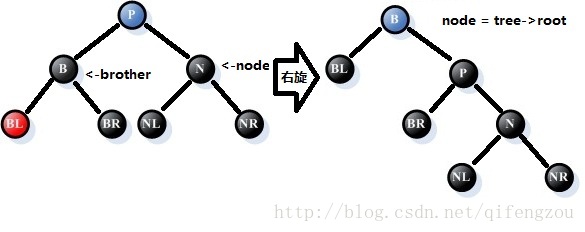
情况8：参照结点N的兄弟B是黑色的，且B的右孩子是黑色的，左孩子是红色的

    处理过程：

        ①、将父结点P的颜色拷贝给兄弟结点B，再将父结点P和兄弟结点的左结点BL颜色改为黑色；

        ②、以父结点P为支点，进行右旋处理；

        ③、将node改为树的根结点，也意味着调整结束。

    如下图所示：[注意：请注意图中处理前后node指针的变化，这将是后续处理的参照]

图12 调整情况8

[注：蓝色表示结点颜色可能为红，也可能为黑，在此也更能突出复制结点P的颜色给结点B]

    综合以上情况的分析，删除结点后的调整过程的实现代码如下所示：[注：代码中出现的数据类型、宏、枚举或函数定义可以参考《算法导论 之 红黑树 - 插入》]

1. /******************************************************************************
2. **函数名称: rbt_delete_fixup
3. **功 能: 修复删除操作造成的黑红树性质的破坏(内部接口)
4. **输入参数:
5. ** tree: 红黑树
6. ** node: 实际被删结点的替代结点(注: node有可能是叶子结点)
7. **输出参数: NONE
8. **返 回: RBT_SUCCESS:成功 RBT_FAILED:失败
9. **实现描述:
10. **注意事项:
11. ** 注意: 被删结点为黑色结点，才能调用此函数进行性质调整
12. **作 者: # Qifeng.zou # 2013.12.28 #
13. ******************************************************************************/
14. int rbt_delete_fixup(rbt_tree_t *tree, rbt_node_t *node)
15. {
16. rbt_node_t *parent = NULL, *brother = NULL;
17.  
18. while(rbt_is_black(node) && (tree->root != node)) {
19. /* Set parent and brother */
20. parent = node->parent;
21.  
22. /* 前提1：node为parent的左孩子 */
23. if(node == parent->lchild) {
24. brother = parent->rchild;
25.  
26. /* Case 1: 兄弟结点为红色: 以parent为支点, 左旋处理 */
27. if(rbt_is_red(brother)) {
28. rbt_set_red(parent);
29. rbt_set_black(brother);
30. rbt_left_rotate(tree, parent);
31.  
32. /* 参照结点node不变, 兄弟结点改为parent->rchild */
33. brother = parent->rchild;
34.  
35. /* 注意: 此时处理还没有结束，还需要做后续的调整处理 */
36. }
37.  
38. /* Case 2: 兄弟结点为黑色(默认), 且兄弟结点的2个子结点都为黑色 */
39. if(rbt_is_black(brother->lchild) && rbt_is_black(brother->rchild)) {
40. rbt_set_red(brother);
41. node = parent;
42. } else {
43. /* Case 3: 兄弟结点为黑色(默认),
44. 兄弟节点的左子结点为红色, 右子结点为黑色: 以brother为支点, 右旋处理 */
45. if(rbt_is_black(brother->rchild)) {
46. rbt_set_black(brother->lchild);
47. rbt_set_red(brother);
48.  
49. rbt_right_rotate(tree, brother);
50.  
51. /* 参照结点node不变 */
52. brother = parent->rchild;
53. }
54.  
55. /* Case 4: 兄弟结点为黑色(默认),
56. 兄弟结点右孩子结点为红色: 以parent为支点, 左旋处理 */
57. rbt_copy_color(brother, parent);
58. rbt_set_black(brother->rchild);
59. rbt_set_black(parent);
60.  
61. rbt_left_rotate(tree, parent);
62.  
63. node = tree->root;
64. }
65. }
66. /* 前提2：node为parent的右孩子 */
67. else {
68. brother = parent->lchild;
69.  
70. /* Case 5: 兄弟结点为红色: 以parent为支点, 右旋处理 */
71. if(rbt_is_red(brother)) {
72. rbt_set_red(parent);
73. rbt_set_black(brother);
74.  
75. rbt_right_rotate(tree, parent);
76.  
77. /* 参照结点node不变 */
78. brother = parent->lchild;
79.  
80. /* 注意: 此时处理还没有结束，还需要做后续的调整处理 */
81. }
82.  
83. /* Case 6: 兄弟结点为黑色(默认), 且兄弟结点的2个子结点都为黑色 */
84. if(rbt_is_black(brother->lchild) && rbt_is_black(brother->rchild)) {
85. rbt_set_red(brother);
86. node = parent;
87. } else {
88. /* Case 7: 兄弟结点为黑色(默认),
89. 兄弟节点的右子结点为红色, 左子结点为黑色: 以brother为支点, 左旋处理 */
90. if(rbt_is_black(brother->lchild)) {
91. rbt_set_red(brother);
92. rbt_set_black(brother->rchild);
93.  
94. rbt_left_rotate(tree, brother);
95.  
96. /* 参照结点node不变 */
97. brother = parent->lchild;
98. }
99.  
100. /* Case 8: 兄弟结点为黑色(默认), 兄弟结点左孩子结点为红色: 以parent为支点, 右旋处理 */
101. rbt_copy_color(brother, parent);
102. rbt_set_black(brother->lchild);
103. rbt_set_black(parent);
104.  
105. rbt_right_rotate(tree, parent);
106.  
107. node = tree->root;
108. }
109. }
110. }
111.  
112. rbt_set_black(node);
113.  
114. return RBT_SUCCESS;
115. }

代码3 删除调整

 

3 处理结果

    首先，随机输入多个key生成左图树，再随机删除任意key后，得到右图树。经过分析可以发现：右图也是一个红黑树。经过反复验证后，可以判断以上代码的处理是正确的。[注：红黑树的打印可以参考博文《算法导论 之 红黑树 - 打印、销毁》]

图13 结果展示

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/RoyalApex/article/details/17608863