Radar Installation
原文是English,直接上中文
Descriptions:
假定海岸线是无限长的直线。陆地位于海岸线的一侧,海洋位于另一侧。每个小岛是位于海洋中的一个点。对于任何一个雷达的安装 (均位于海岸线上),只能覆盖 d 距离,因此海洋中的小岛被雷达安装所覆盖的条件是两者间的距离不超过 d 。
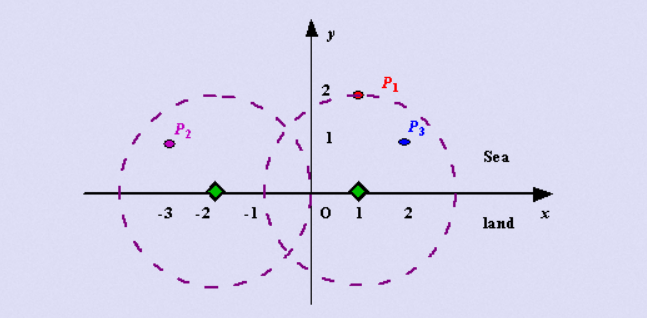
我们使用卡笛尔坐标系,将海岸线定义为 x 轴。海洋的一侧位于 x 轴上方,陆地的一侧位于下方。给定海洋中每个小岛的位置,并给定雷达安装的覆盖距离,您的任务是写一个程序,找出雷达安装的最少数量,使得所有的小岛都被覆盖。注意:小岛的位置以它的 x-y 坐标表示。
Input
输入由多个测试用例组成。每个测试用例的第一行,包含了两个整数 n (1<=n<=1000) 和 d,其中 n 是海洋中小岛的数目,d 是雷达安装的覆盖距离。接下来是 n 行,每行包含了两个整数,表示每个小岛的坐标。每组测试用例之间,以一个空行间隔。
Output
对于每个测试用例,输出一行,包括测试用例的编号,以及雷达安装所需的最小数量。"-1" 个安装,表示该测试用例无解决方案。
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
题目链接:
https://vjudge.net/problem/OpenJ_Bailian-1328
雷达必须在x轴的[s[i].left,s[i].right]之间,每个小岛都有对应在x轴的点是s[i].left和s[i].right,问题转换成用最少的点,使所有的线段都被覆盖到
AC代码:
#include <iostream> #include <cstdio> #include <fstream> #include <algorithm> #include <cmath> #include <deque> #include <vector> #include <queue> #include <string> #include <cstring> #include <map> #include <stack> #include <set> #include <sstream> #define mod 1000000007 #define eps 1e-6 #define ll long long #define INF 0x3f3f3f3f #define ME0(x) memset(x,0,sizeof(x)) using namespace std; struct point { double left,right;//线段两端 bool operator<(const point &c)const//按做端点排序 { return left<c.left; } }; point points[1005]; int n,d; int sum=0; int f=1; //求每个Case int solve() { int ans=1;//雷达个数 double nowpos; sort(points,points+n); // for(int i=0; i<n; i++) // cout<<points[i].left<<" "<<points[i].right<<endl; nowpos=points[0].right; for(int i=1; i<n; ++i) { // cout<<"*"<<endl; if(points[i].left<=nowpos) nowpos=min(nowpos,points[i].right); else//若当前线段与目前线段没有交集,则加入新雷达 { ++ans; nowpos=points[i].right; } } return ans; } int main() { while(cin>>n>>d,n+d) { f=1; sum++; int x,y; for(int i=0; i<n; ++i) { cin>>x>>y; if(y>d) f=0; else { double t=d*d-y*y; points[i].left=x-sqrt(t); points[i].right=x+sqrt(t); } } if(f) printf("Case %d: %d ",sum,solve()); else printf("Case %d: -1 ",sum); } }