【POJ

-->Curling 2.0

 直接上中文

Descriptions:

今年的奥运会之后，在行星mm-21上冰壶越来越受欢迎。但是规则和我们的有点不同。这个游戏是在一个冰游戏板上玩的，上面有一个正方形网格。他们只用一块石头。游戏的目的是让石子从起点到终点，并且移动的次数最小

图1显示了一个游戏板的例子。一些正方形格子可能被砖块占据。有两个特殊的格子，起始点和目标点，这是不占用块。（这两个方块是不同的）一旦石头开始移动就不会停下，除非它击中砖块块。为了使石头到达终点，你可以通过让石块击中墙壁或者砖块来停下。

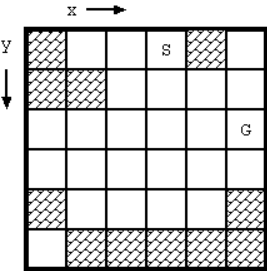
图1：例子（S：开始，G：目标）

石头的运动遵循以下规则：

• 开始时，石头静止起点广场上。
• 石头的运动仅限于x和y方向。禁止对角线移动。
• 当石头静止时，你可以让他向任意方向移动，除非它移动的方向上有砖块（图2（a））。
• 一旦抛出，石头不断向同一方向移动，直到下列事件之一发生：
  • 石头击中砖块（图2（b），（c））。.
    • 石头停在他击中的砖块之前
    • 被击中的砖块消失
  • 石块飞出游戏板之外。
    • 游戏结束的条件
  • 到达目标点
    • 石头停在目标点游戏成功
• 不能在十步之内到达目标点则返回失败。

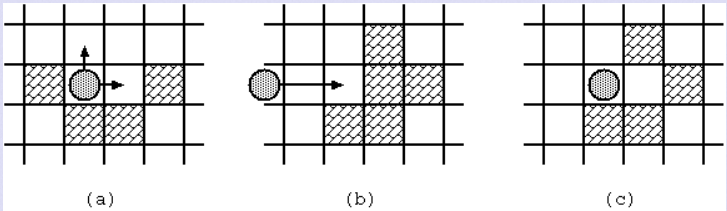
Fig. 2: Stone movements

通过这些规则我们想知道，石头是否能够到达目标点和最少移动次数

初始配置如图1所示，石头从开始到目标需要4次移动。路线如图3所示（a）。注意当石头到达目标时，游戏版的配置如图3（b）改变。

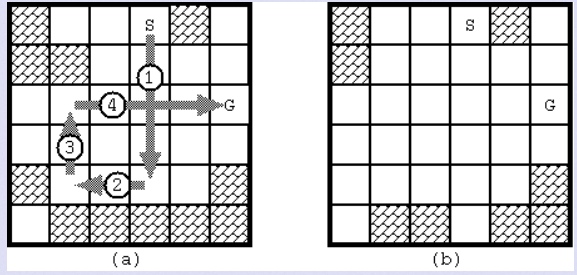
图3：图1的解决方案和解决之后的结果。

Input

输入是一组数据。输入结束标志为两个0。数据组的数量不超过100。

每个数据集如下展示

板的宽度（w）和高度（h） 
游戏版的第一行 
... 
游戏版的h-th行

版的宽和高满足: 2 <= w <= 20, 1 <= h <= 20.

每行由一个空格分隔的十进制数字组成。该数字描述相应的格子的状态。

1 砖块

2 开始点

3 目标点

图. D-1数据如下:

6 6 
1 0 0 2 1 0 
1 1 0 0 0 0 
0 0 0 0 0 3 
0 0 0 0 0 0 
1 0 0 0 0 1 
0 1 1 1 1 1

Output

对于每个数据，打印一个十进制整数的行，表示从开始到目标的路径的最小移动次数。如果没有这样的路线，打印- 1。每个行不应该有这个数字以外的任何字符。

Sample Input

2 1
3 2
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
6 1
1 1 2 1 1 3
6 1
1 0 2 1 1 3
12 1
2 0 1 1 1 1 1 1 1 1 1 3
13 1
2 0 1 1 1 1 1 1 1 1 1 1 3
0 0

Sample Output

1
4
-1
4
10
-1

题目连接：

https://vjudge.net/problem/POJ-3009

dfs+回溯的变形 把每次走一步变成每次走一大行即可

具体看代码

AC代码：

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#include <sstream>
#define mod 1000000007
#define eps 1e-6
#define ll long long
#define INF 0x3f3f3f3f
#define MEM(x,y) memset(x,y,sizeof(x))
#define Maxn 25
using namespace std;
int h,w;//横纵坐标
int sx,sy,ex,ey;//起点 终点坐标
int ans;
int mp[Maxn][Maxn];
int dt[][2]= {{1,0},{-1,0},{0,1},{0,-1}};//4个方向
void dfs(int x,int y,int step) //在(x, y)位置上的步数step
{
    if(x==ex&&y==ey)//到达终点
    {
        if(step<ans)//若有更小值
            ans=step;
        return;
    }
    if(step==10||step>=ans)//若超过10步，或超过当前最短步数
        return;
    for(int i=0; i<4; i++)//四个方向搜索
    {
        int tx=dt[i][0]+x;
        int ty=dt[i][1]+y;
        while(tx>=0&&tx<h&&ty>=0&&ty<w&&mp[tx][ty]!=1)//若此方向能走，则走到尽头，直至出场或撞墙
        {
            if(tx==ex&&ty==ey)//若在过程中到达目标点
            {
                step++;
                if(step<ans)
                    ans=step;
                return;
            }
            tx+=dt[i][0];
            ty+=dt[i][1];
        }
        if((tx==x+dt[i][0]&&ty==y+dt[i][1])||tx<0||tx>=h||ty<0||ty>=w)//此方向不能走，或出场
            continue;
        mp[tx][ty]=0;//撞墙
        step++;
        dfs(tx-dt[i][0],ty-dt[i][1],step);
        step--;//回溯
        mp[tx][ty]=1;
    }
}
int main()
{
    while(cin>>w>>h,w+h)
    {
        ans=11;//初始化
        MEM(mp,0);
        for(int i=0; i<h; i++)
            for(int j=0; j<w; j++)
            {
                cin>>mp[i][j];
                if(mp[i][j]==2)
                {
                    sx=i;
                    sy=j;
                    mp[sx][sy]=0;
                }
                if(mp[i][j]==3)
                {
                    ex=i;
                    ey=j;
                }
            }
        dfs(sx,sy,0);//搜索
        if(ans==11)
            cout<<-1<<endl;
        else
            cout<<ans<<endl;
    }
}