Spark MLib 基本统计汇总 1

1.  概括统计 summary statistics

MLlib支持RDD[Vector]列式的概括统计，它通过调用 Statistics 的 colStats方法实现。

colStats返回一个 MultivariateStatisticalSummary 对象，这个对象包含列式的最大值、最小值、均值、方差等等。

import org.apache.spark.mllib.linalg.Vector
import org.apache.spark.mllib.stat.{MultivariateStatisticalSummary, Statistics}

val observations: RDD[Vector] = ...       // define an RDD of Vectors

// Compute column summary statistics.
val summary: MultivariateStatisticalSummary = Statistics.colStats(observations)
println(summary.mean)                     // a dense vector containing the mean value for each column
println(summary.variance)                 // column-wise variance
println(summary.numNonzeros)              // number of nonzeros in each column

2.  相关性 correlations

1) 基础回顾

协方差：两个变量总体误差的期望。

 

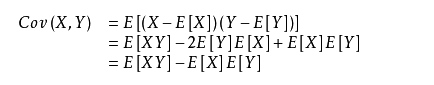
方差是一种特殊的协方差，即两个变量相等时。

所以方差 D(X)=E[X²]-(E(X))²

相关系数：用以反映变量之间相关关系密切程度的统计指标。

其中Cov(X,Y) 是X与Y的协方差，D(X),D(Y) 为其方差。

2）相关性系数的计算

计算两个数据集的相关性是统计中的常用操作，目前Mlib里面支持的有两种：皮尔森(Pearson)相关和斯皮尔曼(Spearman)相关。

Statistics 提供方法计算数据集的相关性。根据输入的类型，两个RDD[Double]或者一个RDD[Vector]，输出将会是一个Double值或者相关性矩阵。

import org.apache.spark.SparkContext
import org.apache.spark.mllib.linalg._
import org.apache.spark.mllib.stat.Statistics
val sc: SparkContext = ...

val seriesX: RDD[Double] = ...                     // a series
val seriesY: RDD[Double] = ...                     // must have the same number of partitions and cardinality as seriesX
val correlation: Double = Statistics.corr(seriesX, seriesY, "pearson")

val data: RDD[Vector] = ...                        // note that each Vector is a row and not a column
val correlMatrix: Matrix = Statistics.corr(data, "pearson")

在上面输入 "pearson" 和"spearman" ，就会计算不同的系数。　

3） Pearson 和Spearman相关系数

Pearson 就是我们平时学到的(是矩相关的一种)。

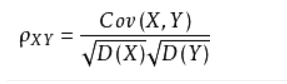
但有限制条件：

• 首先，必须假设数据是成对地从正态分布中取得的；
• 其次，数据至少在逻辑范围内是等距的。

Spearman相关系数，可以操作不服从正态分布的数据集。也就是秩相关（等级相关）的一种。

它是排序变量(ranked variables)之间的皮尔逊相关系数： 即对于大小为n的样本集，将原始的数据X_i和Y_i转换成排序变量rgX_i和rgY_i，再计算皮尔逊相关系数。

3.  分层取样

• 分层抽样法也叫类型抽样法。它是从一个可以分成不同子总体（或称为层）的总体中,按规定的比例从不同层中随机抽取样品（个体）的方法。
• 在 spark.mllib 中，用 key 来分层。
• 分层采样方法 sampleByKey 和 sampleByKeyExact 可以在key-value对的RDD上执行

sampleByKey      ：通过掷硬币的方式决定是否采样一个观察数据， 因此它需要我们传递（pass over）数据并且提供期望的数据大小(size)。

sampleByKeyExact  ：允许用户准确抽取f_k * n_k个样本， 这里f_k表示期望获取键为k的样本的比例，n_k表示键为k的键值对的数量。

                           比每层使用sampleByKey随机抽样需要更多的有意义的资源，但是它能使样本大小的准确性达到了99.99%。

import org.apache.spark.SparkContext
import org.apache.spark.SparkContext._
import org.apache.spark.rdd.PairRDDFunctions

val sc: SparkContext = ...
val data = ... // an RDD[(K, V)] of any key value pairs
val fractions: Map[K, Double] = ... // specify the exact fraction desired from each key

// Get an exact sample from each stratum
val approxSample = data.sampleByKey(withReplacement = false, fractions)
val exactSample = data.sampleByKeyExact(withReplacement = false, fractions)

基础回顾：

泊松分布 Poission分布

   期望和方差均为 λ. 

伯努利分布即二项分布

   期望是np，方差是np(1-p)

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧10,p≦0.1时，就可以用泊松公式近似得计算。

重复抽样用泊松，不重复抽样用伯努利。