“没有测量,就没有科学。”这是科学家门捷列夫的名言。在计算机科学中,特别是在机器学习的领域,对模型的测量和评估同样至关重要。只有选择与问题相匹配的评估方法,我们才能够快速的发现在模型选择和训练过程中可能出现的问题,迭代地对模型进行优化。本文将总结机器学习最常见的模型评估指标,其中包括:
- precision
- recall
- F1-score
- PRC
- ROC和AUC
- IOU
从混淆矩阵谈起
看一看下面这个例子:假定瓜农拉来一车西瓜,我们用训练好的模型对这些西瓜进行判别,显然我们可以使用错误率来衡量有多少比例的瓜被判别错误。但如果我们关心的是“挑出的西瓜中有多少比例是好瓜”,或者“所有好瓜中有多少比例被挑出来了”,那么错误率显然就不够用了,这时我们需要引入新的评估指标,比如“查准率”和查全率更适合此类需求的性能度量。
在引入查全率和查准率之前我们必须先理解到什么是混淆矩阵(Confusion matrix)。这个名字起得是真的好,初学者很容易被这个矩阵搞得晕头转向。下图a就是有名的混淆矩阵,而下图b则是由混淆矩阵推出的一些有名的评估指标。

我们首先好好解读一下混淆矩阵里的一些名词和其意思。根据混淆矩阵我们可以得到TP,FN,FP,TN四个值,显然TP+FP+TN+FN=样本总数。这四个值中都带两个字母,单纯记忆这四种情况很难记得牢,我们可以这样理解:第一个字母表示本次预测的正确性,T就是正确,F就是错误;第二个字母则表示由分类器预测的类别,P代表预测为正例,N代表预测为反例。比如TP我们就可以理解为分类器预测为正例(P),而且这次预测是对的(T),FN可以理解为分类器的预测是反例(N),而且这次预测是错误的(F),正确结果是正例,即一个正样本被错误预测为负样本。我们使用以上的理解方式来记住TP、FP、TN、FN的意思应该就不再困难了。,下面对混淆矩阵的四个值进行总结性讲解:
- True Positive (真正,TP)被模型预测为正的正样本
- True Negative(真负 , TN)被模型预测为负的负样本
- False Positive (假正, FP)被模型预测为正的负样本
- False Negative(假负 , FN)被模型预测为负的正样本
Precision、Recall、PRC、F1-score
Precision指标在中文里可以称为查准率或者是精确率,Recall指标在中卫里常被称为查全率或者是召回率,查准率 P和查全率 R分别定义为:
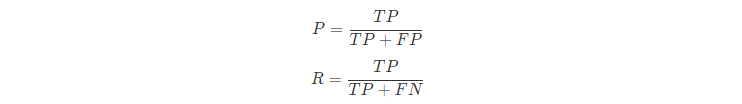
查准率P和查全率R的具体含义如下:
- 查准率(Precision)是指在所有系统判定的“真”的样本中,确实是真的的占比
- 查全率(Recall)是指在所有确实为真的样本中,被判为的“真”的占比
这里想强调一点,precision和accuracy(正确率)不一样的,accuracy针对所有样本,precision针对部分样本,即正确的预测/总的正反例:

查准率和查全率是一对矛盾的度量,一般而言,查准率高时,查全率往往偏低;而查全率高时,查准率往往偏低。我们从直观理解确实如此:我们如果希望好瓜尽可能多地选出来,则可以通过增加选瓜的数量来实现,如果将所有瓜都选上了,那么所有好瓜也必然被选上,但是这样查准率就会越低;若希望选出的瓜中好瓜的比例尽可能高,则只选最有把握的瓜,但这样难免会漏掉不少好瓜,导致查全率较低。通常只有在一些简单任务中,才可能使查全率和查准率都很高。
再说PRC, 其全称就是Precision Recall Curve,它以查准率为Y轴,、查全率为X轴做的图。它是综合评价整体结果的评估指标。所以,哪总类型(正或者负)样本多,权重就大。也就是通常说的『对样本不均衡敏感』,『容易被多的样品带走』。
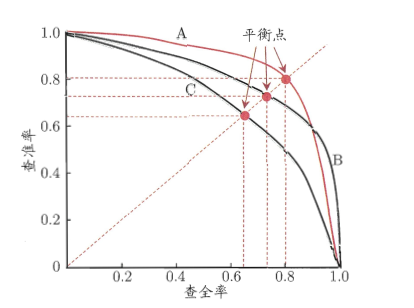
上图就是一幅P-R图,它能直观地显示出学习器在样本总体上的查全率和查准率,显然它是一条总体趋势是递减的曲线。在进行比较时,若一个学习器的PR曲线被另一个学习器的曲线完全包住,则可断言后者的性能优于前者,比如上图中A优于C。但是B和A谁更好呢?因为AB两条曲线交叉了,所以很难比较,这时比较合理的判据就是比较PR曲线下的面积,该指标在一定程度上表征了学习器在查准率和查全率上取得相对“双高”的比例。因为这个值不容易估算,所以人们引入“平衡点”(BEP)来度量,他表示“查准率=查全率”时的取值,值越大表明分类器性能越好,以此比较我们一下子就能判断A较B好。
BEP还是有点简化了,更常用的是F1度量:
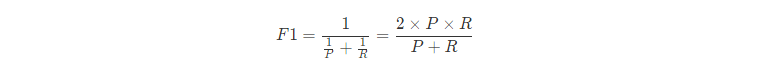
F1-score 就是一个综合考虑precision和recall的指标,比BEP更为常用。
ROC & AUC
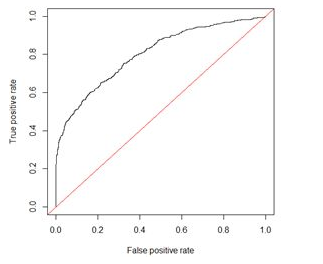
ROC全称是“受试者工作特征”(Receiver Operating Characteristic)曲线,ROC曲线以“真正例率”(TPR)为Y轴,以“假正例率”(FPR)为X轴,对角线对应于“随机猜测”模型,而(0,1)则对应“理想模型”。ROC形式如下图所示。
TPR和FPR的定义如下:
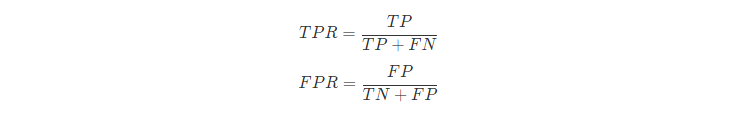
从形式上看TPR就是我们上面提到的查全率Recall,而FPR的含义就是:所有确实为“假”的样本中,被误判真的样本。
进行学习器比较时,与PR图相似,若一个学习器的ROC曲线被另一个学习器的曲线包住,那么我们可以断言后者性能优于前者;若两个学习器的ROC曲线发生交叉,则难以一般性断言两者孰优孰劣。此时若要进行比较,那么可以比较ROC曲线下的面积,即AUC,面积大的曲线对应的分类器性能更好。
AUC(Area Under Curve)的值为ROC曲线下面的面积,若分类器的性能极好,则AUC为1。但现实生活中尤其是工业界不会有如此完美的模型,一般AUC均在0.5到1之间,AUC越高,模型的区分能力越好,上图AUC为0.81。若AUC=0.5,即与上图中红线重合,表示模型的区分能力与随机猜测没有差别。若AUC真的小于0.5,请检查一下是不是好坏标签标反了,或者是模型真的很差。
怎么选择评估指标?
这种问题的答案当然是具体问题具体分析啦,单纯地回答谁好谁坏是没有意义的,我们需要结合实际场景给出合适的回答。
考虑下面是两个场景,由此看出不同场景下我们关注的点是不一样的:
- 地震的预测对于地震的预测,我们希望的是Recall非常高,也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲Precision。情愿发出1000次警报,把10次地震都预测正确了;也不要预测100次对了8次漏了两次。所以我们可以设定在合理的precision下,最高的recall作为最优点,找到这个对应的threshold点。
- 嫌疑人定罪基于不错怪一个好人的原则,对于嫌疑人的定罪我们希望是非常准确的。及时有时候放过了一些罪犯(Recall低),但也是值得的。
ROC和PRC在模型性能评估上效果都差不多,但需要注意的是,在正负样本分布得极不均匀(highly skewed datasets)的情况下,PRC比ROC能更有效地反应分类器的好坏。在数据极度不平衡的情况下,譬如说1万封邮件中只有1封垃圾邮件,那么如果我挑出10封,50封,100...封垃圾邮件(假设我们每次挑出的N封邮件中都包含真正的那封垃圾邮件),Recall都是100%,但是FPR分别是9/9999, 49/9999, 99/9999(数据都比较好看:FPR越低越好),而Precision却只有1/10,1/50, 1/100 (数据很差:Precision越高越好)。所以在数据非常不均衡的情况下,看ROC的AUC可能是看不出太多好坏的,而PR curve就要敏感的多。
IOU
上面讨论的是分类任务中的评价指标,这里想简单讲讲目标检测任务中常用的评价指标:IOU(Intersection over Union),中文翻译为交并比。
这里是一个实际例子:下图绿色框是真实感兴趣区域,红色框是预测区域,这种情况下交集确实是最大的,但是红色框并不能准确预测物体位置。因为预测区域总是试图覆盖目标物体而不是正好预测物体位置。这时如果我们能除以一个并集的大小,就可以规避这种问题。这就是IOU要解决的问题了。

下图表示了IOU的具体意义,即:预测框与标注框的交集与并集之比,数值越大表示该检测器的性能越好。

使用IOU评价指标后,上面提到的问题一下子解决了:我们控制并集不要让并集太大,对准确预测是有益的,这就有效抑制了“一味地追求交集最大”的情况的发生。下图的2,3小图就是目标检测效果比较好的情况。

参考资料: