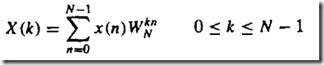
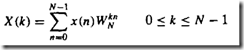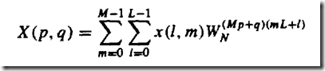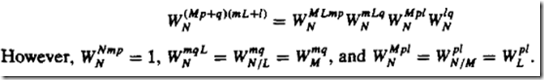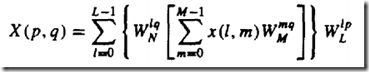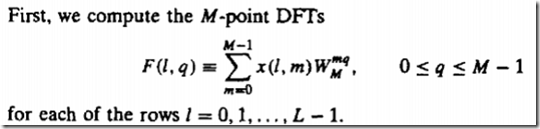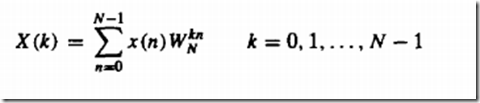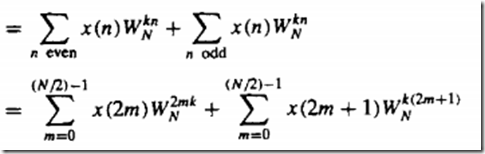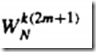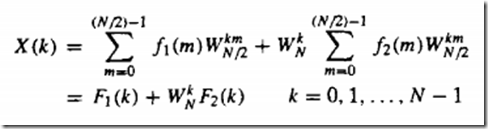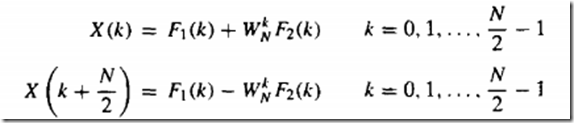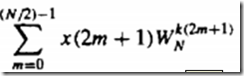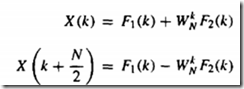WN=e^(-j*2*pi/N)
DFT复杂度o(N^2)
降低与N^2的依赖 使N = LM (L^2+m^2 <= N^2)
N点DFT分解为M段L点DFT
一维的N点序列变为(L,M)二维序列,每一行分别进行DFT
举例两种一维到二维的映射关系
n = Ml+m
| 1 | 3 | 5 | 7 | 9 |
| 2 | 4 | 6 | 8 | 10 |
n = l+mL
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
与之所求的DFT 也可存入相对应的(q,p)矩阵中
以第一种(n = Ml+m)为例:k = Mp+q
找书麻烦这里给出推到:
重一维到二维
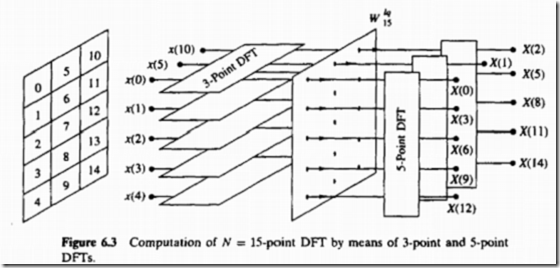
两种流程:
按列存入信号
计算每行M点DFT
乘以相位因子
计算每一列的L点DFT
按行读取所得数组
图示:
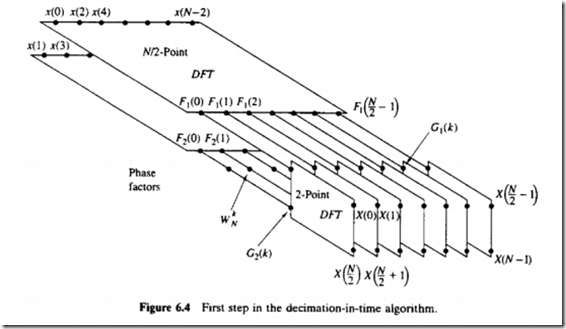
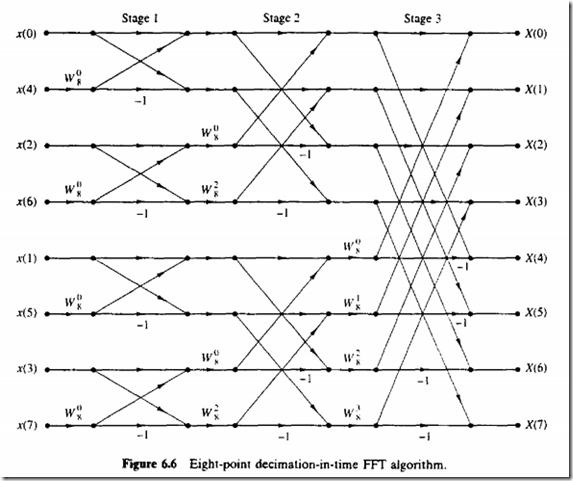
来看下基2_FFT算法:
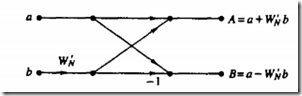
上图的N/2点的dft可以分解为N/4的而N/4的DFT可以分解为N/8的……直到最后分解为2点的DFT
这儿的2点DFT其实是输出A+B,A-B两个值
为什么可以这样分解呢?其实他就是1个数学式子的’分解‘过程,来看下
N点的DFT是这玩意儿
将序列 奇偶分开
X(2m) 可看为f(m)
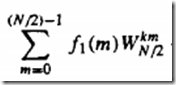 而这个可看作一个新的N/2点DFT ------------可见N点的DFT已经分解为N/2点DFT
而这个可看作一个新的N/2点DFT ------------可见N点的DFT已经分解为N/2点DFT
由采样定理,在频域上(N/2以为新的周期)F(k+N/2)=F(k),且,![]() 。
。
所以得出下式:
复数乘法运算量![]() 。而原始DFtT的量为N^2,当N够大时几乎减小了一半
。而原始DFtT的量为N^2,当N够大时几乎减小了一半
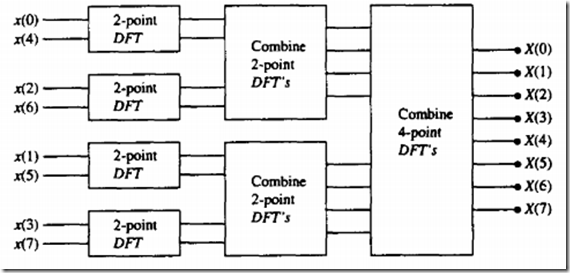
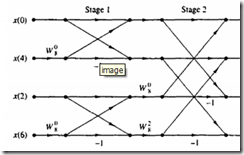
这是举例看下8点DFT的奇偶分解
| 一级dft(抽第二级奇偶) | 二级dft(抽第三极的奇偶) | 第三极dft(最终) |
| 0 | 0 | 0 |
| 4 | 2 | 1 |
| 2 | 4 | 2 |
| 6 | 6 | 3 |
| 1 | 1 | 4 |
| 5 | 3 | 5 |
| 3 | 5 | 6 |
| 7 | 7 | 7 |
可用二进制倒序实现 即011100变为001110,感觉镜像啦下