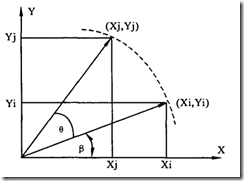
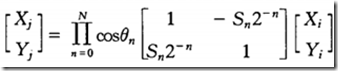
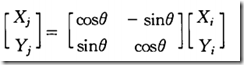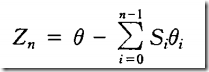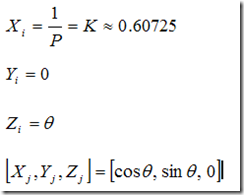该系统完成的是一个平面坐标旋转如图 1所示,可以看出,将向量(X i ,Y i ) 旋转![]() 角,得到一个新的向量
角,得到一个新的向量
( Xj,Yj)。
硬件上用乘除法很耗资源,未来节省资源采用这样的思路:最常用的代替乘法的方式是移位运算
来看下把这乘法最终转换为移位的思路:
移位运算只能做乘除2. 但这些运算组合可形成大的乘除法
将要旋转的角度分解,每次完成一小块,多次后就可逼近角度值
分解(逼近)方式入下:
 第n次的旋转角度必须是这个(n为任意值)(arctan(1)= 45度)
第n次的旋转角度必须是这个(n为任意值)(arctan(1)= 45度)
 Sn为符号(-,+)
Sn为符号(-,+) ,各种
,各种![]() 组合成
组合成![]() (即真正要旋转的角度)
(即真正要旋转的角度)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 随着迭代的增加他将收敛与常数K(或1/P),故可用预先计算来消除.
随着迭代的增加他将收敛与常数K(或1/P),故可用预先计算来消除.
··········································································································································································
未旋转的角度减少到0,用伪代码表示为
For n=0 to [inf]
If (Z(n) >= 0) then
Z(n + 1) := Z(n) – atan(1/2^n);
Else
Z(n + 1) := Z(n) + atan(1/2^n);
End if;
End for;
预先计算好arctan(1/2^n)的值,形成查找表的形式,[inf]为需要的迭代次数,每一位需要1次(16轮的迭代将产生16位的结果),如果加入X,Y的计算,用伪代码的表示如下:
For n=0 to [inf]
If (Z(n) >= 0) then
X(n + 1) := X(n) – (Yn/2^n);
Y(n + 1) := Y(n) + (Xn/2^n);
Z(n + 1) := Z(n) – atan(1/2^n);
Else
X(n + 1) := X(n) + (Yn/2^n);
Y(n + 1) := Y(n) – (Xn/2^n);
Z(n + 1) := Z(n) + atan(1/2^n);
End if;
End for;
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
使Z趋向于0
存在以下有趣的情况:
注意:参数范围
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
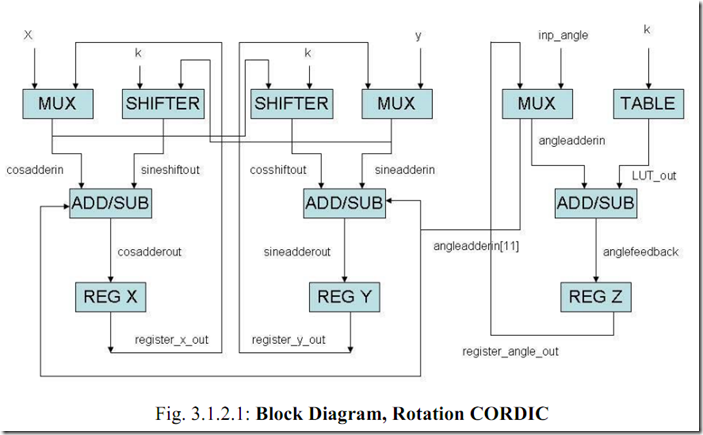
算法硬件实现原理图:
X,Y的输入为最原始的x,y值;k的输入为确定arctan(1/2^k) ; ![]() 要旋转的角度
要旋转的角度
数据最高位为符号位1为负 0为正
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
![]() ···
··· ···
···

 ····
···· 这个反馈回路来完成迭代,一次次小的旋转最终完成大的旋转
这个反馈回路来完成迭代,一次次小的旋转最终完成大的旋转
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

 这个回路····· Z(n + 1) := Z(n) +atan(1/2^n);
这个回路····· Z(n + 1) := Z(n) +atan(1/2^n);
Z(n + 1) = Z(n) -atan(1/2^n);
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If (Z(n) >= 0) then
X(n + 1) := X(n) – (Yn/2^n);
Y(n + 1) := Y(n) + (Xn/2^n);
Z(n + 1) := Z(n) – atan(1/2^n);
Else
X(n + 1) := X(n) + (Yn/2^n);
Y(n + 1) := Y(n) – (Xn/2^n);
Z(n + 1) := Z(n) + atan(1/2^n);
End if;
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
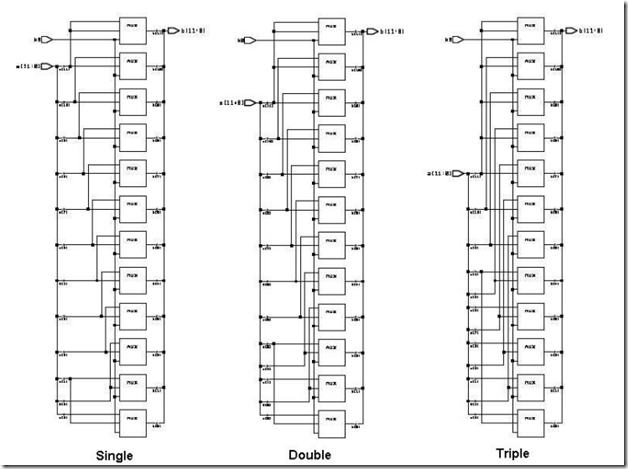
先给出RTL的图:
思路:
这里k有三位,故整个移位过程分3步进行 即 single ; double; triple
这三部分是将数依次移动 2^0, 2^1, 2^2
实例:
k = 3’b101;
k[0] = 1; 故数右移1*2^0位
k[1] = 0; 故数右移0*2^1位
k[2] = 1; 故数右移1*2^2位
k控制的的选择器
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Look-Up Table
这儿用12位2进制数表示角度(bit[11],bit[10]……bit[0])
首先确定12位数与角度的关联:
bit[11] 表示-180度 (1:出现-180;0:不出现-180; 方便与后边的数累加 即可表示-180~ +180的值)
bit[10] 表示+90度
bit[9:0] 表示+90/(2^n)
(n值得确定方式为:
1 为bit[9]
`
`
`
10 为bit[0]
)(其实就是角度减半减半再减半)
verilog 描述:
另外由于旋转因子需要进行0°、-90°或+90°三种预旋转,所以预旋转还要分配两位二进制数,这样存储旋转系数就为12位的
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
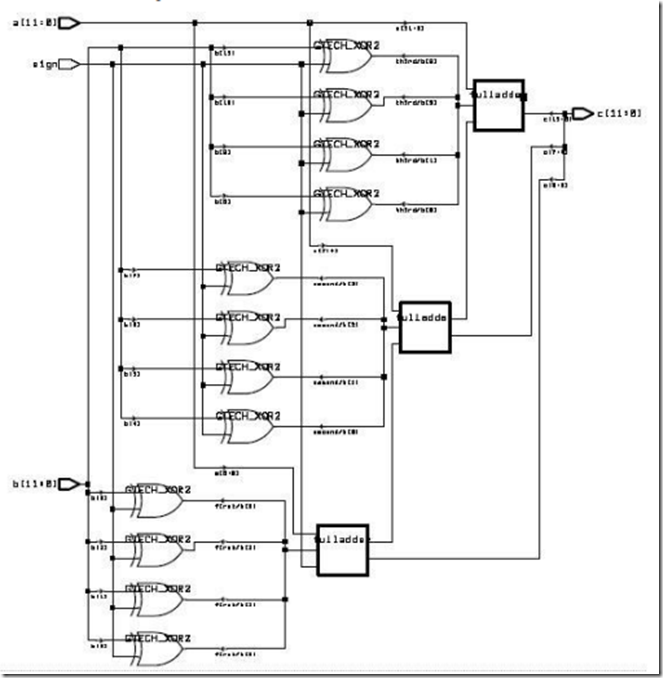
12-bit Full Adder
有点像异或门做选择器,呵呵
![]() 二进制与1异或 相当于取反 取反后二进制的位置与原先的位置是对称的 故可以此表示-180 ~ +180
二进制与1异或 相当于取反 取反后二进制的位置与原先的位置是对称的 故可以此表示-180 ~ +180
当与0异或时 原数不变
当sign = 0 时做加法
当sign = 1 时做减法 (其实是改变后的加法)
这个4位的全加器就多讲啦
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
·~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~``
最后:
Vectoring CORDIC 用于计算复数的模
用迭代使Y趋向0 就是将矢量旋转到x轴上 此时x轴坐标就是 矢量的模;
需要注意的是:
在迭代之前要保证矢量在(-90,,90)之间
操作方法是 当矢量在地1,2象限(0,180)是-90度
当矢量在地3,4象限(-180,0)时+90度
参考资料: