盛最多水的容器

题目

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

示例 1：

输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。示例 2：

输入：height = [1,1] 输出：1 示例 3：

输入：height = [4,3,2,1,4] 输出：16 示例 4：

输入：height = [1,2,1] 输出：2

解题思路

双指针法

可以知道，容器的盛水量 = 两端当中短的一端高度 * 两端之间的距离

这可谓之 短板原理。即两板之间所盛水量由短的一端决定。

比如下面这种情况

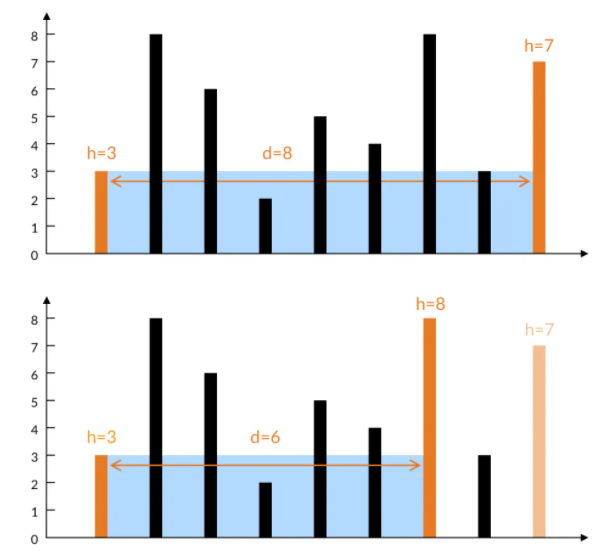
代码

package main

import "fmt"

func Cap(list []int) int {
	start, end := 0, len(list) -1

	res := 0
	for start < end {
		if list[start] < list[end] {
			res = Max(res, list[start]*(end - start))
			start ++
		} else {
			res = Max(res, list[end]*(end- start))
			end --
		}
	}

	return res
}

func Max(x, y int) int {
	if x > y {
		return x
	}

	return y
}



func main() {
	ss := []int{1,8,6,2,5,4,8,3,7}
	res := Cap(ss)
	fmt.Println(res)
}

　　地址：https://mp.weixin.qq.com/s/auiILwKKHJ79nSC6SNyj3A