题目描述
一列火车n节车厢,依次编号为1,2,3,…,n。每节车厢有两种运动方式,进栈与出栈,问n节车厢出栈的可能排列方式有多少种。
输入
一个数,n(n<=60000)
输出
一个数s表示n节车厢出栈的可能排列方式
题解:
这题要用大数,java
然后卡特兰数:有个数学模型 s[i]=c(n,2n)/(n+1)
组合数公式:这个总是记不住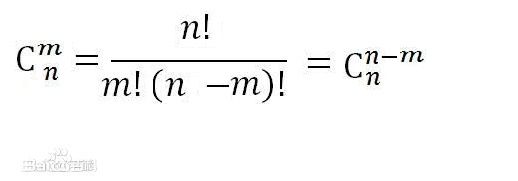
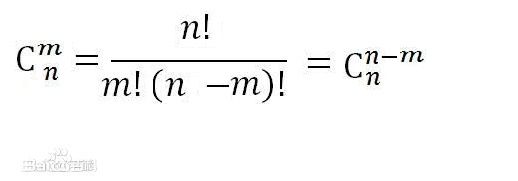
这个题不能直接求,会TLE。需要先求出结果的每个质因数有多少次幂,然后用快速幂求,再把所有求幂得到的结果乘起来。
http://www.cnblogs.com/sciorz/p/9263122.html

import java.math.*; import java.util.*; public class Main {//筛法求素数 static final int maxn=120050; static boolean[]isprime=new boolean[maxn]; static int[] prime=new int[maxn]; static int pz=0; static void getPrime() { for(int i = 2; i < maxn; ++i) isprime[i]=true; for(int i = 2; i < maxn; ++i) { if(isprime[i]) prime[pz++]=i; for(int j = 0; j < pz&&(long)i*prime[j]<maxn; ++j) { isprime[i*prime[j]]=false; if(i%prime[j]==0) break; } } } static Scanner cin=new Scanner(System.in); static int n=0; public static void main(String[] args) { n=cin.nextInt(); getPrime(); BigInteger ans=B(1); for(int i = 0; i < pz&&prime[i]<=2*n; ++i) { int cnt=0,p=prime[i]; int t=n*2; while(t>0) {//(2n!) cnt+=t/p; t/=p; } t=n; while(t>0) {//(n!*n!) cnt-=t/p*2; t/=p; } ans=ans.multiply(pow(p,cnt)); } System.out.println(ans.divide(B(n+1))); } static BigInteger pow(int x,int n) {//快速积 BigInteger ans=B(1),base=B(x); while(n>0) { if(n%2==1) ans=ans.multiply(base); base=base.multiply(base); n>>=1; } return ans; } static BigInteger B(int x) { return BigInteger.valueOf(x); } }
