1.冒泡排序
比较相邻的元素,如果第一个比第二个大,则交换这两个的值,对每一对相邻的元素进行同样的操作,从第一对到最后一对,这样最大的元素就到最后面了。对于所有的元素再次进行同样的操作,不断重复,最后就会完成排序。
原理图:

void sort(int *a,int size) { int i,j,tmp; for(i=0;i<size-1;i++) { for(j=0;j<size-i-1;j++) { if(a[j] > a[j+1]) { tmp = a[j]; a[j] = a[j+1]; a[j+1] = tmp; } } } }
2.选择排序
选定第一个元素作为标志位,后面的元素插进来时都要与它进行比较,如果是升序排序的话,比它大的就放后面,比它小的就放前面,将标志位改为比它小的元素,始终保证最前面的元素是最小的;降序排序就反过来,比它小的直接放后面,比它大的放前面,再将标志位改为比它大的元素。从第一个元素开始为标志位,下一轮的标志位是第二个元素(前面的已经排好序了),之后第三个,第四个....直到最后一个。这样就排好序了。
//选择排序--升序 void select_sort(int *arr,int size) { for(int i=0;i<size;i++) { for(int j=i+1;j<size;j++) { if(arr[i] > arr[j]) { int t = arr[i]; arr[i] = arr[j]; arr[j] = t; } } } }
3.插入排序
插入排序比较直观一点,跟选择排序有点类似,第二个元素与第一个元素进行比较,大的放后面,小的放前面,这样前面两个就已经排好序了,第三个元素就从第一个元素开始比较,比第一个小就放在前面,比第二个大就放在后面,否则就放在中间,之后的每一个元素都是这样,分别与前面已经排好的每一个元素进行比较,最后放在比它小并且后面的值比它大的位置。(升序)
void insert_sort(int *a,int size) { int i,j,tmp; for(i=1;i<size;i++) { if(a[i]<a[i-1]) { tmp = a[i]; for(j=i-1;j>=0 && a[j] > tmp;j--) { a[j+1] = a[j]; } a[j+1] = tmp; } } }
4.快速排序
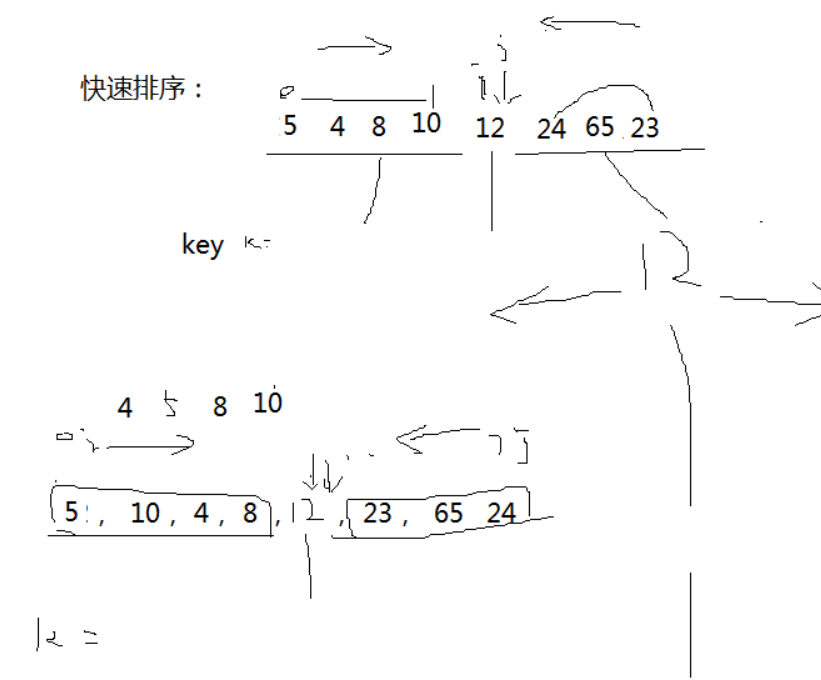
基本思想:第一遍排序将数列分成两个部分,前半部分比中间的key值小,后半部分比中间的key值大,然后再在两部分之间再找个key值,再分别进行排序,不断的分成两部分,最后排序完成。
步骤:从数列中挑出一个key值(随便选),分别从数列两端开始比较,i、j分别指向数列第一个和最后一个元素,第i个元素如果比key小,则i指向下一个元素,直到指向一个比key大的元素,然后把该元素跟key交换位置,交换之后,key还是原来的值,只是位置变了;接下来i不动,从最后一个元素开始,j指向的元素跟key比较,元素比key小,就交换位置,比key大则j指向前面一个元素,直到遇到比key小的元素;交换之后又从i开始....i跟j轮流开始,直到i=j,在把key的值填入这个位置,这样整个数列就以key分成两半了。接下来用同样的方法,在前半部和后半部分别找个key进行排序。
int quick_sort(int *a,int low,int high) { if(low < high) { int i = low; int j = high; int k = a[low]; while(i < j) { while(i < j && a[j] >= k) { j--; } if(i < j) { a[i++] = a[j]; } while(i < j && a[i] < k) { i++; } if(i < j) { a[j--] = a[i]; } } a[i] = k; //递归调用 quick_sort(a,low,i-1); quick_sort(a,i+1,high); } }
5.希尔排序
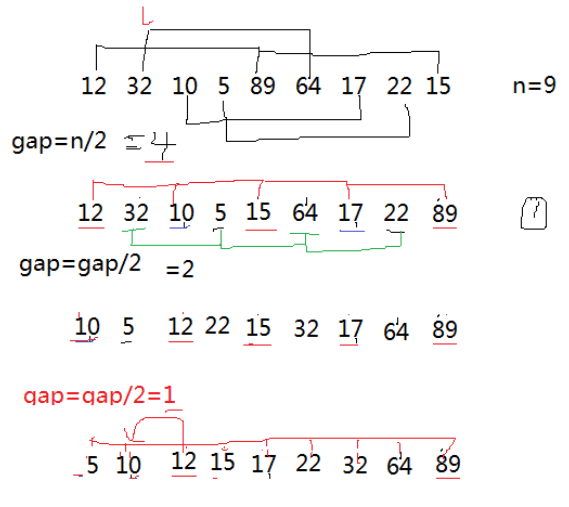
基本思想:希尔排序实际上是插入排序的改进版,在插入排序的基础上增加了分组,会优先比较距离比较远的元素,又被称为缩小增量排序。
步骤:按一定的间隔进行划分数列,然后在每一组中进行插入排序,第一次的间隔为size/n,即每隔(size/n)的距离取一个数字,将这些数字分为一组,就有很多组,分别进行快速排序,这些数组在原来的大的数列中的位置并没有变,只是每一小组中的位置换了而已,例如:第一组的位置是第1、4、7个位置,这个小组内部排好序之后的数字也是按顺序填入这三个位置中。第二次为size/2n...直到间隔为1,之后再排一次插入排序就可以了。
void shell_sort(int a[],int n) { int i,j,k; int tmp,gap; for(gap = n/2;gap > 0;gap /=2)//选取步长 { for(i = 0;i < gap;i++)//直接插入排序 { for(j = i+gap;j < n;i+=gap)//每次都加上步长 { if(arr[j] < arr[j-gap]) { tmp = arr[j]; k = j-gap; while(k >= 0 && arr[k] > tmp)//记录后移 { arr[k+gap] = arr[k]; k-=gap; } arr[k+gap] = tmp;//找到位置插入 } } } }
6.归并排序
基本思想:归并排序是建立在归并操作上的排序算法,将数列分成很多的小的数列,将小数列内部排好序之后,再两两合并成多个数列,这些数列内部再进行排序,再两两合并...最后排好序了,其他排序都不需要额外申请空间,归并排序需要申请空间。
步骤:将长度为n的数列分成两个长度为n/2的子数列,将这两个子数列再进行拆分,变成四个子数列,这四个子数列内部排好序后,前两个跟后两个子数列分别合并并且排序,得到两个排好序的子数列,再进行合并并且排序,就得到一个完整的排好序的数列了。

//分组归并 void merge(int arr[],int begin1,int end1,int begin2,int end2,int tmp[]) { int k = begin1; int i = begin1,j = begin2; while(i <= end1 && j <= end2) { if(a[i] <= a[j]) tmp[k++] = a[i++]; else tmp[k++] = a[i++]; } //将左边的元素放到tmp中 while(i <= end1) tmp[k] = a[i++]; while(j <= end2) tmp[k++] = a[j++]; //将tmp中的数据拷贝到愿数组中相应的区间 memcpy(a+begin1,tmp+begin1;sizeof(int)*(end2-begin1+1)); } //归并排序 void merge_sort(int *a,int ldft,int dight,int *tmp) { if(lefi > = right)return; //mid将数组一分为二 int mid = left + ((right - left)>>1); //左边归并排序,不断递归 mergsort(a,left,mid,tmp); //右边归并排序,不断递归 mergsort(a,mid+1,right,tmp); //合并两个子数组 merge(a,left,mid,mid+1,right,tmp); }
7.二叉树排序
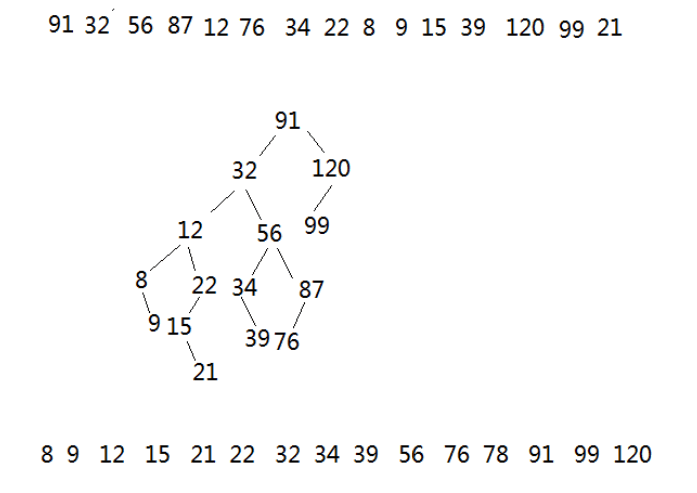
基本思想,创建一个二叉树序树(把第一个数字放在根节点,取后面的数字与根节点比较,大的放右边,小的放左边),然后中序遍历得到有序数列。
#include <stdio.h> #include <sys/time.h> #include <stdbool.h> #include <stdlib.h> int get_random_data(int type) { //1.获取系统时间 struct timeval tv; gettimeofday(&tv, NULL); //设置随机数因子 srandom(tv.tv_usec); return random()%type; } //设计一个树结构 typedef struct BTree{ int data; struct BTree *lchild; struct BTree *rchild; }Bitree; Bitree* create_tree_node(int data) { Bitree * root = (Bitree*)malloc(sizeof(Bitree)); root->lchild = NULL; root->rchild = NULL; root->data = data; return root; } Bitree *create_sort_tree(Bitree* root, int data) { if(root == NULL) { root = create_tree_node(data); return root; } //root不为空 if(data > root->data)//把data插入到右边 { root->rchild = create_sort_tree(root->rchild, data); } else//插入根的左边 { root->lchild = create_sort_tree(root->lchild, data); } return root; } void mid_tree(Bitree* root) { if(root == NULL)return ; if(root->lchild != NULL) { mid_tree(root->lchild); } printf("%d ", root->data); if(root->rchild != NULL) { mid_tree(root->rchild); } } int main(void) { Bitree *root = NULL; for(int i=0; i<100; i++) { int data = get_random_data(100); printf("%d ", data); root = create_sort_tree(root, data); } printf(" "); //通过中序号遍历 mid_tree(root); printf(" "); return 0; }
还有什么堆排序、计数排序、桶排序,都太难了,我不会,就不写了。
8.各种排序的复杂度如下图所示(下面这部分是引用自某不认识大佬的博客的图图片,地址贴在后面)
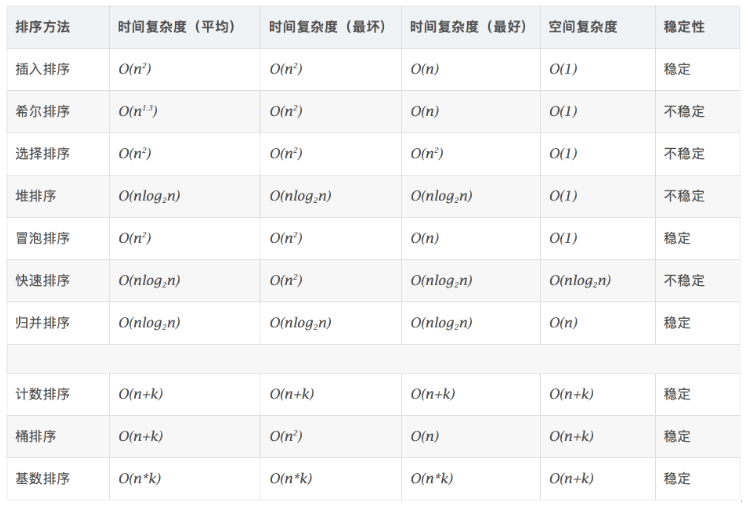
稳定:如果a原本在b的前面,而a=b,排序之后a仍然在b的前面。
不稳定:同上,但是排序后a在b的后面。
时间复杂度:对排序算法的总操作次数,反应出当要排序的数列长度n变化时,操作次数呈现的规律。
空间复杂度:指的是算法在计算机内执行的时候所需的存储空间的度量,也是数据规模为n的函数。
PS:如果我哪里写错了,请指正,互相学习一下。
复杂度的那部分内容转自:https://www.cnblogs.com/onepixel/articles/7674659.html