来看一道最大流模板水题,借这道题来学习一下最大流的几个算法。
分别用Edmond-Karp,Dinic ,SAP来实现最大流算法。
从运行结过来看明显SAP+当前弧优化+gap优化速度最快。
hiho一下 第115周:网络流一•Ford-Fulkerson算法
原题网址:http://hihocoder.com/contest/hiho115/problem/1
网络流一·Ford-Fulkerson算法
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho住在P市,P市是一个很大很大的城市,所以也面临着一个大城市都会遇到的问题:交通拥挤。
小Ho:每到周末回家感觉堵车都是一种煎熬啊。
小Hi:平时交通也还好,只是一到上下班的高峰期就会比较拥挤。
小Ho:要是能够限制一下车的数量就好了,不知道有没有办法可以知道交通系统的最大承受车流量,这样就可以限制到一个可以一直很顺畅的数量了。
小Hi:理论上是有算法的啦。早在1955年,T.E.哈里斯就提出在一个给定的网络上寻求两点间最大运输量的问题。并且由此产生了一个新的图论模型:网络流。
小Ho:那具体是啥?
小Hi:用数学的语言描述就是给定一个有向图G=(V,E),其中每一条边(u,v)均有一个非负数的容量值,记为c(u,v)≥0。同时在图中有两个特殊的顶点,源点S和汇点T。
举个例子:
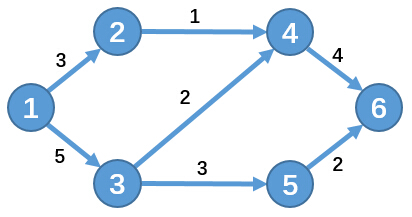
其中节点1为源点S,节点6为汇点T。
我们要求从源点S到汇点T的最大可行流量,这个问题也被称为最大流问题。
在这个例子中最大流量为5,分别为:1→2→4→6,流量为1;1→3→4→6,流量为2;1→3→5→6,流量为2。
小Ho:看上去好像挺有意思的,你让我先想想。
提示:Ford-Fulkerson算法
输入
第1行:2个正整数N,M。2≤N≤500,1≤M≤20,000。
第2..M+1行:每行3个整数u,v,c(u,v),表示一条边(u,v)及其容量c(u,v)。1≤u,v≤N,0≤c(u,v)≤100。
给定的图中默认源点为1,汇点为N。可能有重复的边。
输出
第1行:1个整数,表示给定图G的最大流。
样例输入
6 7
1 2 3
1 3 5
2 4 1
3 4 2
3 5 3
4 6 4
5 6 2
样例输出
5
一、Ford-Fulkerson算法
算法讲解与图片均摘自:http://hihocoder.com/contest/hiho115/problem/1
设f(u,v)实际流量,c(u,v)为每条路径的容量。
整个图G的流网络满足3个性质:
1. 容量限制:对任意u,v∈V,f(u,v)≤c(u,v)。
2. 反对称性:对任意u,v∈V,f(u,v) = -f(v,u)。
3. 流守恒性:对任意u,若u不为S或T,一定有∑f(u,v)=0,(u,v)∈E。
对于上面例子中的图,其对应的实际流量f网络图为:
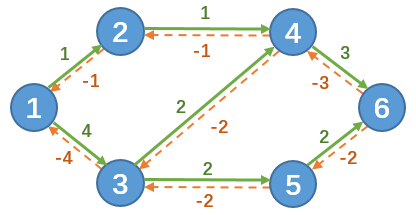
其中绿边表示例子中每条边实际使用的流量f(u,v),虚线表示实际不存在的边(v,u)。
在此基础上,假设我们用cf(u,v)来表示c(u,v)-f(u,v),则可以表示每一条边还剩下多少的流量可以使用,我们称为残留容量。
假设一条边(u,v),其容量为3,即c(u,v)=3,由于边(u,v)单向,(v,u)容量为0,c(v,u)=0。
使用了流量f(u,v)=2(同时有f(v,u)=-2)
则可以表示为:cf(u,v)= c(u,v)-f(u,v)=1, cf(v,u)= c(v,u)- f(v,u)=2。
由cf(u,v)构成的图我们称为残留网络。
比如例子中的残留网络图为:
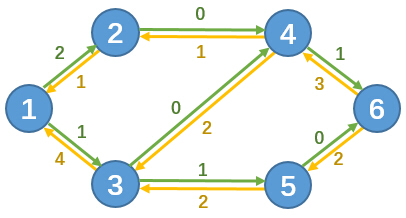
残留网络表示还可以使用的流量。
如果能从残留网络中找出一条从S到T的路径p,使得路径p上所有边的cf(u,v)都大于0,假设路径p上最小的cf(u,v)等于k,就可以使得S到T增加k的流量。
通过该条路径p使得图G的最大流得到了增加,这样的路径p被称为增广路径。
Ford-Fulkerson算法的流程:
1. 将最初的图G转化为残留网络。
2. 在残留网络上寻找增广路径。
l 若存在增广路径,最大流量增加,同时对增广路径上的边cf(u,v)进行修改(总流量增加,路径上各边容量相应减少,反向边容量相应增加),再重复寻找增广路径。
l 若不存在增广路径,则这个图不能再增加流量了,得到最大流。
Ford-Fulkerson算法确定了解决最大流问题的基本思路,接下来的关键就是算法的实现,如何寻找增广路并实现路径的修改。
二、Edmond-Karp算法
Edmond-Karp算法的思路其实就是Ford-Fulkerson算法。
Edmond-Karp流程:
1. 将最初的图G转化为残留网络。
2. 使用BFS反复寻找源点到汇点之间的增广路径。
若存在增广路径,对路径上的流量进行相应修改(总流量增加,路径上各边容量相应减少,反向边容量相应增加)。
3. 找不到增广路时,当前的流量就是最大流。
#include <algorithm> #include <cstring> #include <string.h> #include <iostream> #include <list> #include <map> #include <set> #include <stack> #include <queue> #include <string> #include <utility> #include <vector> #include <cstdio> #include <cmath> #define LL long long #define N 40005 using namespace std; const int maxn=505; const int inf=0x7fffffff; struct Edge{ int u,v,c; int next; }edge[N]; int cnt;//边数 int head[N]; void addedge(int u,int v,int c) { edge[cnt].u=u; edge[cnt].v=v; edge[cnt].c=c; //正向边初始化为容量 edge[cnt].next=head[u]; head[u]=cnt++; edge[cnt].u=v; edge[cnt].v=u; edge[cnt].c=0; //反向边容量初始化为0 edge[cnt].next=head[v]; head[v]=cnt++; } bool visit[maxn]; // 记录结点i是否已访问 int pre[maxn]; //记录路径 int m,n; int source,sink; //源点,汇点 bool bfs() //寻找从源点到汇点的增广路,若找到返回true { queue<int>q; memset(pre,-1,sizeof(pre)); memset(visit,false,sizeof(visit)); pre[source]=-1; visit[source]=true; q.push(source); while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u];i!=-1;i=edge[i].next) { int v=edge[i].v; if(edge[i].c>0&&!visit[v]) { pre[v]=i; visit[v]=true; if(v==sink) return true; //存在增广路 q.push(v); } } } return false; } int Edmond_Karp() { int maxflow=0; int delta; while(bfs()) //反复在源点到汇点间寻找增广路 { delta=inf; int i=pre[sink]; while(i!=-1) { delta=min(delta,edge[i].c); //路径上最小的容量为流量增量 i=pre[edge[i].u]; } i=pre[sink]; while(i!=-1) { // 路径上各边容量相应减少,反向边容量相应增加,总流量增加 edge[i].c-=delta; //增广路上的边减去使用的容量 edge[i^1].c+=delta; //同时相应的反向边增加残余容量 i=pre[edge[i].u]; } maxflow+=delta; } return maxflow; } int main() { while(scanf("%d%d",&n,&m)!=EOF) { int u,v,w; memset(head,-1,sizeof(head)); for(int i=0;i<m;i++) { scanf("%d%d%d",&u,&v,&w); addedge(u,v,w); } source=1,sink=n; printf("%d ",Edmond_Karp()); } return 0; }
三、Dinic算法
Dinic算法的流程:
利用BFS对残余网络分层。每个节点的层数就是源点到这个节点经过的最少边数。
用DFS 寻找增广路。DFS每向下走一步必到达层数+1的节点,(标记满足dep[v]=dep[u]+1的边(u,v)为允许弧,增广路只走允许弧)。
找到增广路并相应修改后,回溯后继续寻找增广路,回溯到源点且无法继续,DFS结束
重复以上过程直到BFS分层到达不了汇点,结束。
Dinic算法《北京大学ACM暑期课讲义-网络流》讲的挺清楚的
#include <algorithm> #include <cstring> #include <string.h> #include <iostream> #include <list> #include <map> #include <set> #include <stack> #include <queue> #include <string> #include <utility> #include <vector> #include <cstdio> #include <cmath> #define N 40005 using namespace std; int const inf = 0x3f3f3f3f; int const MAX = 505; struct Edge{ int u,v,c; int next; }edge[N]; int cnt;//边数 int head[N]; void addedge(int u,int v,int c) { edge[cnt].u=u; edge[cnt].v=v; edge[cnt].c=c; edge[cnt].next=head[u]; head[u]=cnt++; edge[cnt].u=v; edge[cnt].v=u; edge[cnt].c=0; edge[cnt].next=head[v]; head[v]=cnt++; } int n, m; int dep[MAX]; //分层 int source,sink; //源点,汇点 int bfs()//BFS对残余网络分层 { queue<int> q; while(!q.empty()) q.pop(); memset(dep, -1, sizeof(dep)); dep[source] = 0; //源点层数初始化为0 q.push(source); while(!q.empty()){ int u = q.front(); q.pop(); for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].v; if(edge[i].c> 0 && dep[v] == -1) { dep[v] = dep[u] + 1; q.push(v); } } } return dep[sink] != -1; //BFS分层是否能到达汇点 } int dfs(int u, int delta)//DFS 寻找增广路,一次DFS可以寻找多条增广路 { if(u == sink) //找到增广路 return delta; int flow=0; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].v; if(edge[i].c> 0 && dep[v] == dep[u] + 1){ //dfs从前一层向后一层寻找增广路 int tmp = dfs(v, min(delta-flow, edge[i].c)); // 路径上各边容量相应减少,反向边容量相应增加,总流量增加 edge[i].c -= tmp; edge[i^1].c+= tmp; flow+=tmp; } } if(!flow) dep[u]=-1*inf; return flow; } int dinic() { int ans = 0, tmp; while(bfs()){ while(1){ tmp = dfs(1, inf); if(tmp == 0) break; ans += tmp; } } return ans; } int main() { while(~scanf("%d %d", &n, &m)){ cnt=0; memset(head,-1,sizeof(head)); int u, v, c; while(m--){ scanf("%d %d %d", &u, &v, &c); addedge(u,v,c); } source=1,sink=n; printf("%d ", dinic()); } return 0; }
四、SAP 算法
基础思路还是残余网络分层,寻找增广路。和Dinic思路类似。
不过SAP分层只需要反向BFS一次。
关键在于Gap优化,当前弧优化。
Gap优化:
gap[i]表示dep[x]=i节点的个数。
如果一次重标号时,出现gap[i]=0,即出现断层,则源点到汇点之间出现断路,到达不了,结束算法。
当前弧优化:
对于每个点保存“当前弧”。
当前弧初始化是邻接表的第一条弧,即head[i],查找边的过程中找到一条允许弧,允许弧设为当前弧。
搜索边的过程从当前弧开始搜,因为可以保证每个点当前弧之前的边都不是允许弧。
代码参考:http://blog.csdn.net/sprintfwater/article/details/7913181
#include <algorithm> #include <cstring> #include <string.h> #include <iostream> #include <list> #include <map> #include <set> #include <queue> #include <string> #include <utility> #include <vector> #include <cstdio> #include <stdio.h> #include <cmath> #define LL long long #define N 40005 using namespace std; const int maxn=505; const int inf=0x7fffffff; struct Edge{ int u,v,c; int next; }edge[N]; int cnt; int head[N]; void addedge(int u,int v,int c) { edge[cnt].u=u; edge[cnt].v=v; edge[cnt].c=c; edge[cnt].next=head[u]; head[u]=cnt++; edge[cnt].u=v; edge[cnt].v=u; edge[cnt].c=0; edge[cnt].next=head[v]; head[v]=cnt++; } int m,n; int source,sink; //源点,汇点 int gap[maxn]; //gap优化 int dep[maxn]; //层数 int cur[maxn]; //当前弧优化 int path[maxn]; //用一个栈储存增广路路径 void rev_bfs() //对残余网络逆向分层 { memset(dep,-1,sizeof(dep)); memset(gap,0,sizeof(gap)); queue<int>q; dep[sink]=0; //汇点sink的深度为0 gap[0]=1; // 层数为0的点有1个 q.push(sink); while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u];i!=-1;i=edge[i].next) { int v=edge[i].v; if(edge[i^1].c>0&&dep[v]==-1) { q.push(v); dep[v]=dep[u]+1; gap[dep[v]]++; } } } } int SAP() { rev_bfs(); //只需要bfs分层一次,之后的层数更新不用重新bfs // for(int i=1;i<=n;i++) cout<<dep[i]<<endl; memcpy(cur, head,sizeof(cur)); //当前弧初始化是邻接表的第一条弧,即head[i] int maxflow = 0; int u=source; int top=0; int i; while (dep[source] < n) //最大的层数只会是n,如果大于等于n说明中间已经断层了 { if (u==sink) //找到了一条增广路,则沿着增广路修改流量 { int delta=inf; int flag=n; //flag记录增广路上容量最小的边 for (i=0; i!=top; i++){ if (delta>edge[path[i]].c) { delta=edge[path[i]].c; flag=i; } } for (i=0;i!=top;i++) // 路径上各边容量相应减少,反向边容量相应增加,总流量增加 { edge[path[i]].c-=delta; edge[path[i]^1].c+=delta; } maxflow += delta; top = flag; //回溯到流量恰好变为0的最上层节点,继续寻找增广路 u = edge[path[top]].u; } for (i = cur[u]; i != -1; i = edge[i].next) { int v=edge[i].v; if (edge[i].c>0 && dep[u]==dep[v]+1) break; } if (i!=-1) //找到一条允许弧 { cur[u]=i; //允许弧设为当前弧 path[top++]=i; u=edge[i].v; } else //找不到允许弧,重新分层,再寻找增广路 { //对u节点层数进行修改 if (--gap[dep[u]] == 0) break;// gap优化,如果出现断层,结束算法 int mind = n+1; for (i = head[u]; i != -1; i = edge[i].next) //寻找可以增广的最小层数 { if (edge[i].c>0 && mind>dep[edge[i].v]) { mind=dep[edge[i].v]; cur[u]=i; //允许弧设为当前弧 } } dep[u]=mind+1; //更新层数 gap[dep[u]]++; u=(u==source)? u : edge[path[--top]].u; //回溯 } } return maxflow; } int main() { while(~scanf("%d%d",&n,&m)) { int u,v,w; cnt=0; memset(head,-1,sizeof(head)); for(int i=0;i<m;i++) { scanf("%d%d%d",&u,&v,&w); addedge(u,v,w); } source=1,sink=n; printf("%d ",SAP()); } return 0; }