「对比型数据」和「分布型数据」的可视化
1.学习目的
- 了解数据之间的对比关系,可以通过哪些「标记+视觉通道」映射,从而来表现差异;
- 熟练掌握表示数据对比关系的图形类型,以及这些图形的适用场景、异同;
- 熟悉描述性统计的相关内容,掌握分布型数据可视化的常用图表和适用场景;
- 实践:给定2个数据集,选择合适的图表并进行可视化呈现,实现工具不限;
2前言
- 「对比型数据」:对比两组或两组以上数据的差异。
- 「分布型数据」:研究数据分布的集中趋势、离散程度、偏态和峰度等。
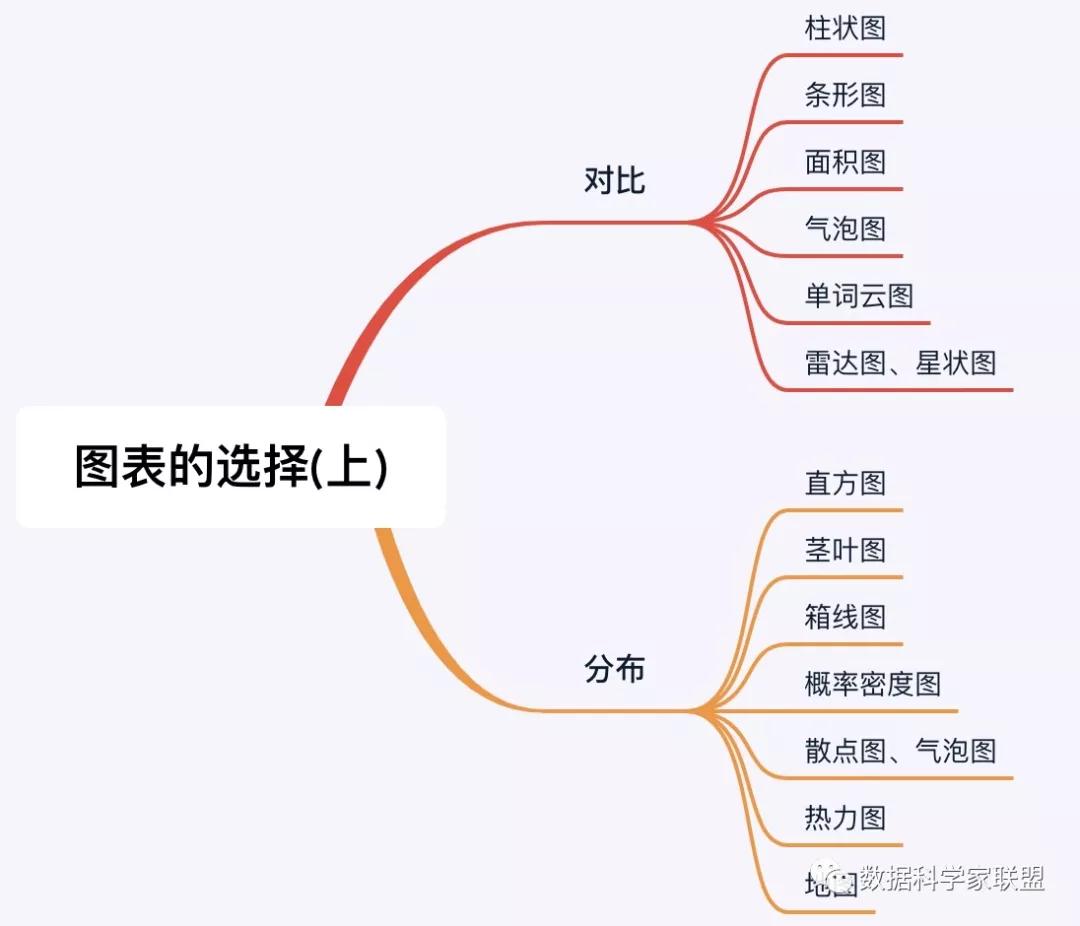
3.对比型数据可视化
一般来说,对比多组数据之间的差异,我们是通过不同的标记和视觉通道体现出来的.
- 高度差异/宽度差异:柱状图、条形图。
- 面积差异:面积图、气泡图。
- 字号差异:单词云图。
- 形状差异:星状图。
3.1 柱状图
柱状图可以使离散时间数据可视化的方式之一,系列值的数据类型是时间.
柱状图除了可以用于离散时间数据的可视化,更多的是用于比较不同分类数据的可视化,且柱状图的数据条数,最好不要超过12条。
以下根据数据类别的个数和可视化的目的,细化柱状图的图表选择:
- 单一柱状图:适合单一类别的数据比对,也适合表示离散型时序数据的趋势。
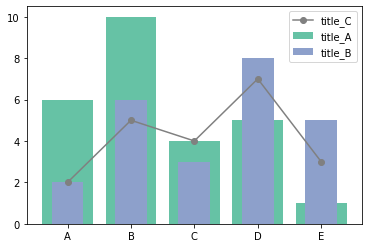
- 重叠型柱状图:适合两个类别的数据对比,半透明柱形条,代表某项指标的「目标值」,内部偏窄且不透明的柱形条表示某项指标的「实际完成情况」。通常会搭配折线图使用,折线图则表示目标完成率。
- 并列柱状图:适合两个或三个数据类别的对比,若数据类别超出3个,不建议使用并列柱状图。
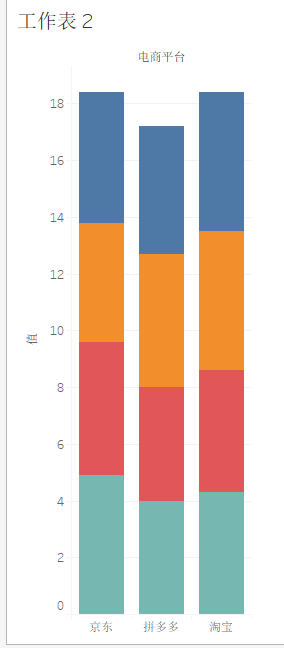
- 堆叠柱状图:适合既要对比总体的数据,又要对比总体各构成项的数据,但是总体各构成项一般不要大于5个,若大于5个,可按占总体的比例进行归类,展示TOP5的分类,剩下则归为「其他」。

3.2 条形图
条形图,可以视为是柱状图的一种变体,在大部分情况下,是可以互换的。那么在哪些情况下,条形图能比柱状图更好的展示数据呢?
- 条形图,相比柱状图而言,可以展示更多的数据条数,一般不要超过30条。
- 若分类项的文本过长时,柱状图的文本需要进行旋转才能不重叠,不利于阅读,而条形图就就没有这个缺点。

3.3 面积图
面积图,是折线图的一种延伸,其实就是折线图和折线图投影到X轴的直线所围成的面积。
按照对比方式的不同,面积图可以分为:「重叠对比型面积图」和「堆砌对比型面积图」,两者的区别如下。
- 重叠对比型:所有系列的面积基线都是X轴,系列之间有重叠和覆盖的关系。
- 堆砌对比型:只有底层系列的面积基线和X轴重合,其他系列都是堆砌在它们下面一组的数据上面。
面积图用来做什么?
面积图,一般也是用于趋势分析中。
当需要分析各个系列,随时间的变化趋势时,此时使用「重叠对比型面积图」比较合适;当既需要分析整体随时间的变化趋势,又要了解整体的各构成项随时间的变化趋势时,使用「堆砌对比型面积图」比较合适。
因为数据里没有时间,这里就不放上去了.
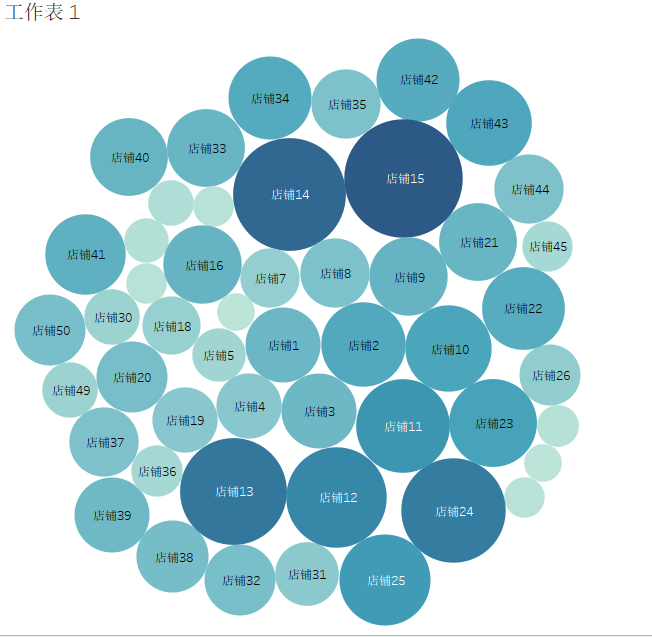
3.4 气泡图
气泡图,和散点图的区别是,气泡图一般是用于三维数据的可视化,而散点图是用于二维数据的可视化。
在散点图中,圆点的面积是相同的,主要是通过圆点在坐标轴中的坐标点(X,Y)确定的位置,来映射数据。
而气泡图,是通过气泡的面积大小来对比数据的图形方式,它除了可以反映散点图中坐标点X、Y的相关关系,还有一个维度的数据可以映射到气泡的面积大小上,因此「气泡图」可以在二维平面展示三维信息的数据。
当只有一个系列时,只需要一种气泡图只需要一种颜色即可。当有多个系列时,不同系列之间可以用颜色来区别。

3.5 单词云图
单词云图,主要是用于网络文本中词频数据的可视化,如关键词搜索,文章高频词,热点事件关键词等。
单词云图,是通过单词的字号大小来反映词频的大小,字号越大,词频越高。通常,为了达到贴合主体的特征,以及视觉美观的目的,用户可以自定义单词云的配色方案、背景形状等设计层面的个性化。
图
通过单词云图,用户可以快速找出网站搜索的高频词汇、了解文章的主旨、get到热点事件的关键信息。但是要注意一点,单次云图只适合表示一组文本数据的对比,不适合多个类别的文本数据之间的比较。

3.6 雷达图/星状图
当需要对比一个主体、或多个主体本身,在不同维度上的特征时,雷达图和星状图是不错的选择。
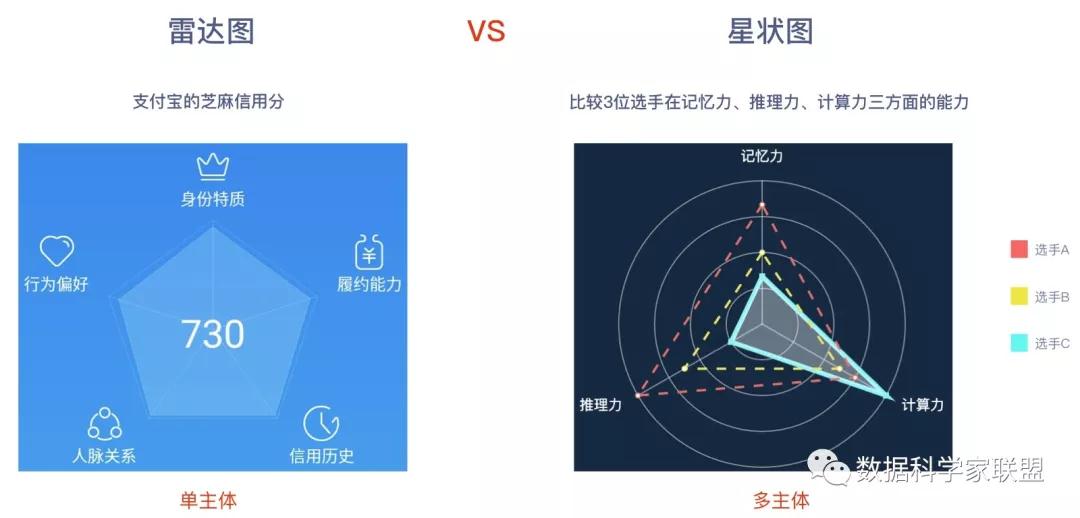
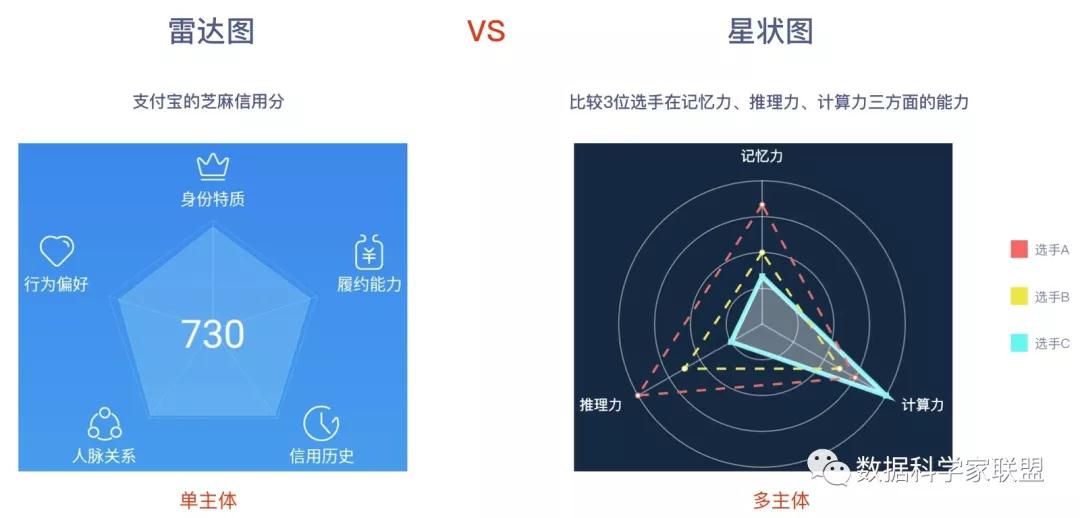
雷达图和星状图的区别是:
- 雷达图是一体多维的数据,即可视化的对象是一个主体,只是这个主体具有多个维度上的数据特征。对比的是,同一个主体,在不同维度上的数值,可以看出主体在不同维度上的偏向。
- 星状图是多体多维的数据,即可视化的对象是多个主体,且多个主体维度相同,且单个主体具有多个维度上的数据特征。对比的是,多个主体,在同一维度上的数值,可以看出不同主体之间的差异和侧重点。
简单理解就是,雷达图可以视为是星状图中的一行记录。而且,一般情况下,会给予不同维度上的数值一定的权重,从而算出各个主体的综合得分,我们的芝麻信用分就是这么来的。
4.分布型数据可视化
补充:统计学第1篇-描述性统计
4.1 直方图
直方图有频数直方图和频率直方图.都是展示离散型分布数据的情况.
绘制直方图的步骤:
绘制直方图,有如下几步:
- 首先,要对数据进行分组,然后统计每个分组内数据元的频数和频率。
- 其次,在平面直角坐标系中,横轴标出每个组数据的下限和上限,即上图中的a和b。
- 最后,纵轴表示频数或频率,每个矩形的高代表对应的频数或频率,即上图中的h。
若纵轴表示的是频数,则是「频数直方图」;若纵轴展示的是「频率」,则为「频率直方图」,如上图所示。
「频数分布直方图」中,频数乘以组距得出每个分组的数量,可以看出频数分布直方图是用面积来表示频数的,和柱状图(条形图)是用长方形的高度(宽度)表示数量是有本质性区别的。
4.2 茎叶图
茎叶图一般适合数据为整数的数据的可视化.
举例,图.
4.3 箱线图
在描述性统计中,有涉及到分位数相关的知识,其中比较常用的是四分位数,即一组数据中的下四分位数Q1、中位数、上四分位数Q3.
一组数据中的四分位数,加上这组数据的最大值、最小值,这5个特征值,就可以绘制一个箱线图。
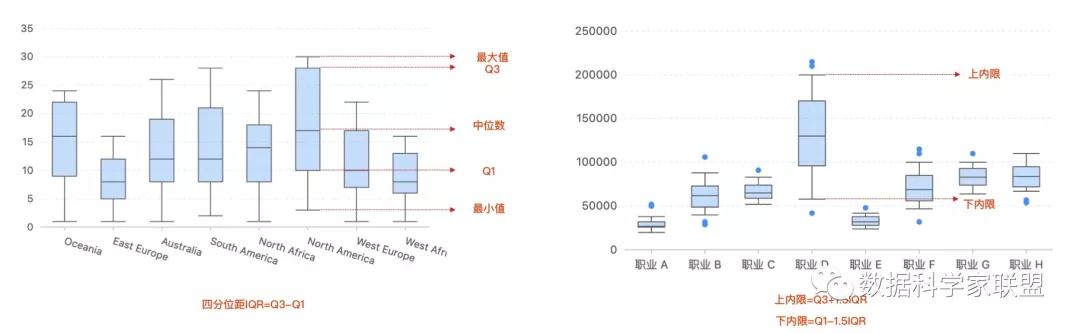
箱线图释义:
- 箱子的中间一条线,是数据的中位数,代表了样本数据的平均水平。
- 箱子的上下限,分别是数据的上四分位数Q3和下四分位数Q1,这代表箱体部分包含了数据集中50%的数据,因此,箱子的宽度(四分位距=Q3-Q1)在一定程度上反映了数据的离散程度。
- 在箱子的上方和下方,又各有一条线,有时候代表着最大最小值,有时候代表的是上下内限。如果有点位于内限之外,理解成“异常值”就好。
箱线图常用场景:
(1)对比多组数据的分布情况。
(2)检测数据中的异常值或离群点。
股市中很多的...
4.4 概率密度图
用于描述连续型随机变量其分布规律.
在数学中,连续型随机变量的概率密度函数是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数,简单理解就是,连续型随机变量取值某个确定数值的概率,即为纵切直线与概率密度函数交点的纵坐标的值。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分,也就是区间的上下限与概率密度曲线围成的面积。通过图形化的方式,我们可以清楚的看到随机变量分布的对称性情况,以及随机变量取值是集中还是分散,这些可以通过偏态系数和峰度系数来度量。
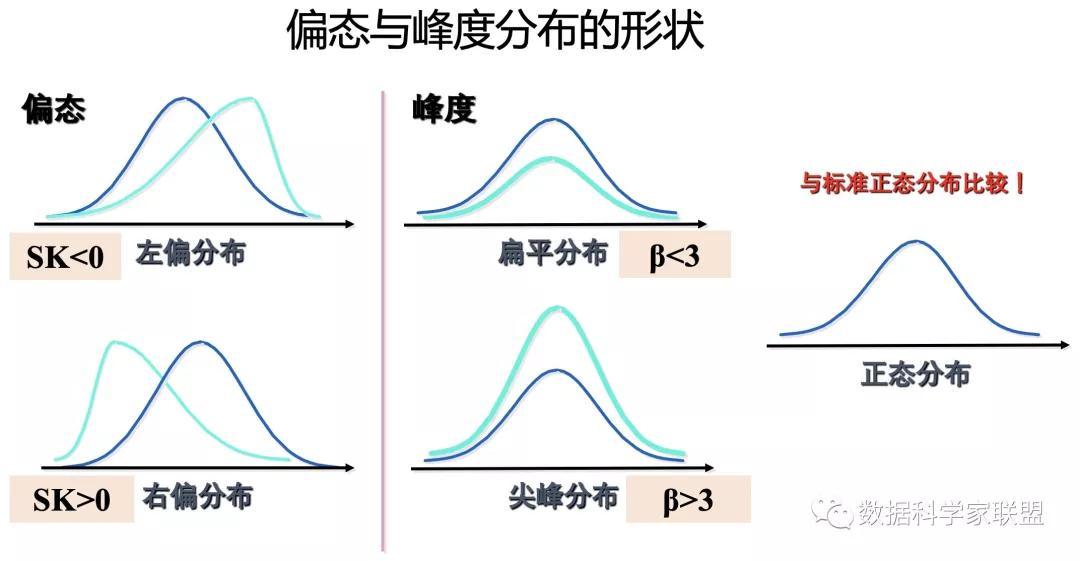
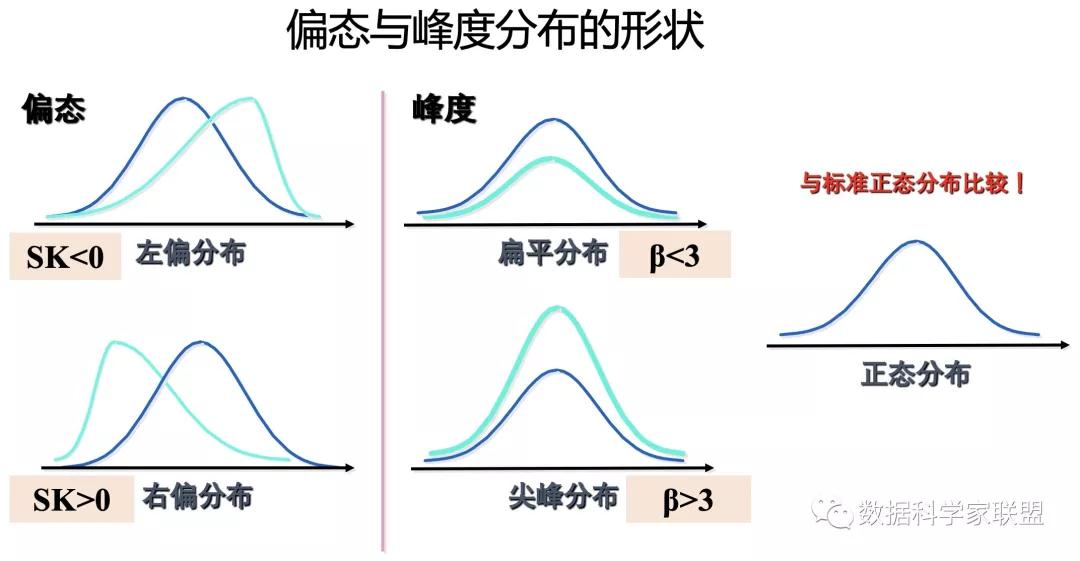
4.5 散点图/气泡图
参上.
散点图和气泡图的区别:
- 散点图,一般是用于研究两个变量之间的相关关系,可以是一个类别数据,也可以是多类别数据,但是都是二维的数组(x,y)。
- 气泡图,除了具体散点图的功能以外,还可以用气泡的面积来映射第三个维度的数据,对应的数据形式是(x,y,z),同样可以用于多组或多类别数据的比较。
4.6 热力图
热力图,是通过密度函数进行可视化,用于表示地图中点的密度的热图。现阶段,热力图在地图、网页分析、业务数据分析等其他领域也有较为广泛的应用。
- 热力地图:比如我们日常使用的导航APP,通过热力图来表示各个路况的拥挤程度,颜色越深表示人员越多,对应路段也就越拥挤,有了热力图可以很直观的看到区域内的人群流量,方便驾车人士进行路线规划。
- 网页热力分析:常见的网页热力图,有按鼠标点击位置的热力图、按鼠标移动轨迹的热力图、按内容点击的热力图。还有一种是获取用户眼球在屏幕上的移动轨迹热力图,不过这种因为涉及到用户隐私,获取数据的难度很大。通过网页热力分析,可以直观清楚地看到页面上每一个区域的访客兴趣焦点,从而为营销推广、用户体验优化提供依据。
- 业务数据分析:带有地理信息属性的数据、或者离散时间属性的数据,也可以使用热力图来进行数据展示。
4.7 地图
当数据带有地理型信息属性时,首选的可视化图表为地图。按照展示的数据空间划分,地图可以分为二维平面地图和三维立体地图。
比如我们常用的导航软件、天气预报、降水量、台风移动路线等都和地理信息相挂钩,这些数据一般也是在地图上进行呈现,给人以直观的视觉体验。
5.总结
无论是要对比数据,还是研究数据的分布情况,都需要根据数据的类型、数据的特征来确定可视化的最佳方式。
根据数据之间的关系、分析目的、数据特征,来选择和确定相应的图表类型,这个是可视化过程中需要牢牢把握的要点。图表的目的,是为了更直观、准确的呈现数据背后的信息和知识,不同数据关系应该选择什么图表都是有套路的可循的。
但是,如果只是为了使用某个觉得高大上的图表,而不管数据的特征是否适用,则是舍本逐末的做法,最终的可视化效果也必定是不理想的。
6.作业
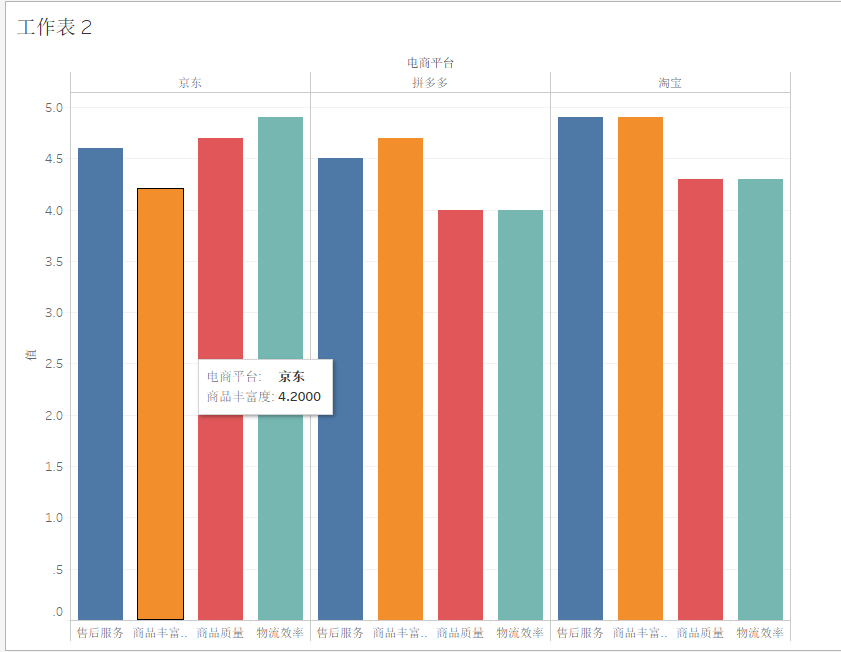
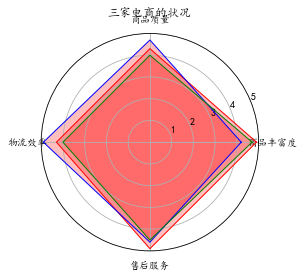
6.1 电商
明显用雷达图.这里没法把多系列的情况标记出来,因此效果大打折扣,哪位同学会请教教我.谢谢!
6.2 公司店铺月度收入,成本和综合评分
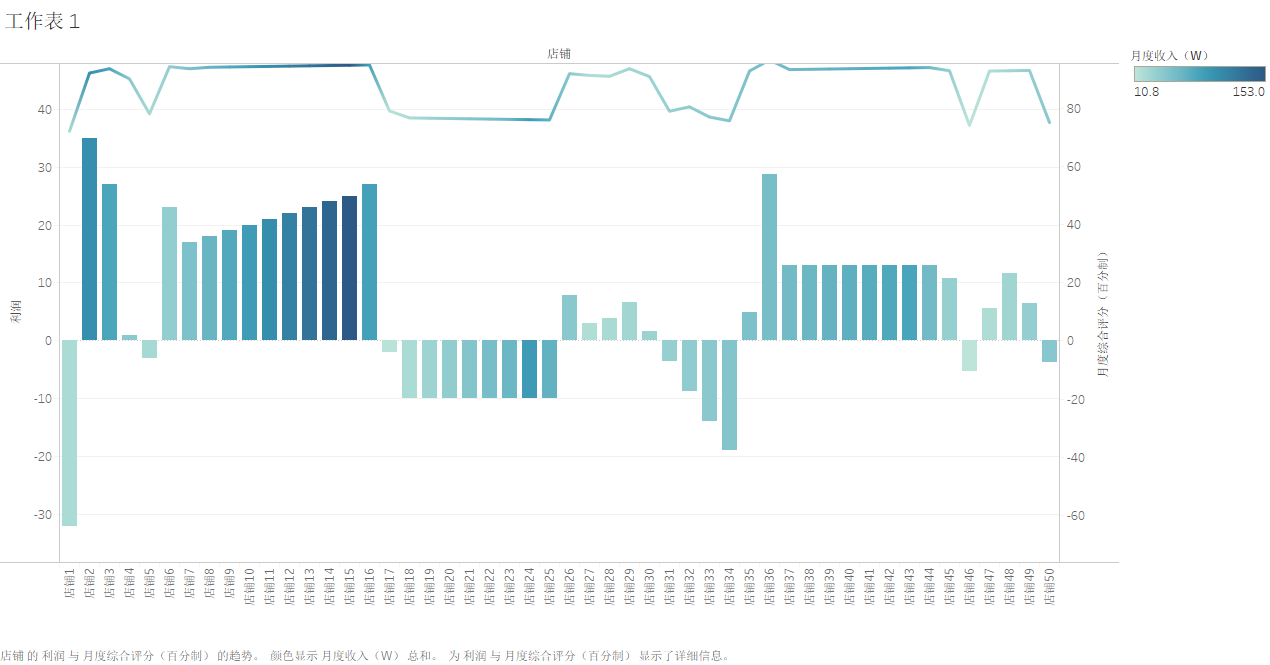
用tableau做,简单明了.

参考链接:
木东居士---如何优雅地选择数据图表:对比型和分布型数据图表
Tableau技巧(30):巧妙实现 双柱图 和 折线图 的组合图表