排序方法:插入、选择、交换、归并、分配排序
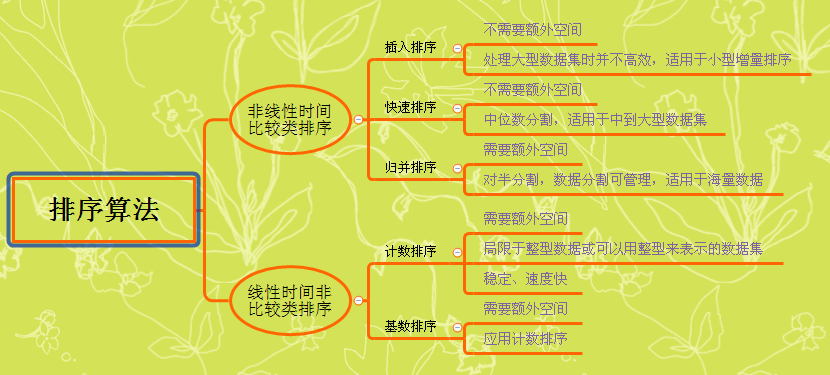
插入排序
直接插入排序
流程图:
代码实现:
void InsertSort(int *a,int len){
for(int i=1;i<len;i++){
int j=i-1;
//需要插入的数据
int temp=a[i];
//当插入的数据小于前面的数据时
while(temp<a[j]&&j>=0){
//将插入的数据的前面的数据向后移动
a[j+1]=a[j];
j--;
}
//插入数据
a[++j]=temp;
}
}
特点:数据有序程度越高,越有效
适应场景:小规模数据或者基本有序时十分高效。
希尔排序
流程图:
代码实现:
void shellSort(int *a,int len){
//gap是分组步长,temp是哨兵
int i,j,k,temp,gap;
for(gap=len/2;gap>=1;gap/=2){
//以gap为间隔分组
for(i=0;i<gap;i++){
//每一组做插入排序
for(j=i+gap;j<length;j=j+gap){
//如果当前元素比这一组中的前一个元素要小
if(array[j]<array[j-gap]){
//记录当前这个更小的元素 temp
temp = array[j]; //哨兵
k = j - gap;
//把这一组中之前所有比temp小的元素都往后挪一个位置
while(k>=0 && array[k]>temp){
array[k + gap] = array[k];
k = k - gap;
}
//把挪出来的空位,放入temp
array[k + gap] = temp;
}
}
}
}
}
交换排序
冒泡排序
代码实现:
void bubbleSort(int a[], int n) { //下面是函数bubbleSort的程序
//定义三个整型变量
int i,j,temp;
//用一个嵌套循环来遍历一遍每一对相邻元素 (所以冒泡函数慢嘛,时间复杂度高)
for (j=0;j<n-1;j++){
for (i=0;i<n-1-j;i++) {
if(a[i]>a[i+1]) { //从大到小排就把左边的">"改为"<" !!!
temp=a[i]; //a[i]与a[i+1](即a[i]后面那个) 交换
a[i]=a[i+1]; //基本的交换原理"c=a;a=b;b=c"
a[i+1]=temp;
}
}
}
}
快速排序(双向指针)
流程图:8

代码实现:
void quicksort(int left, int right) {
int i, j, t, temp;
if(left > right)
return;
temp = a[left]; //temp中存的就是基准数
i = left;
j = right;
while(i != j) { //顺序很重要,要先从右边开始找
while(a[j] >= temp && i < j)
j--;
while(a[i] <= temp && i < j)//再找右边的
i++;
if(i < j)//交换两个数在数组中的位置
{
t = a[i];
a[i] = a[j];
a[j] = t;
}
}
//最终将基准数归位
a[left] = a[i];
a[i] = temp;
quicksort(left, i-1);//继续处理左边的,这里是一个递归的过程
quicksort(i+1, right);//继续处理右边的 ,这里是一个递归的过程
}
选择排序
直接选择排序
流程图:
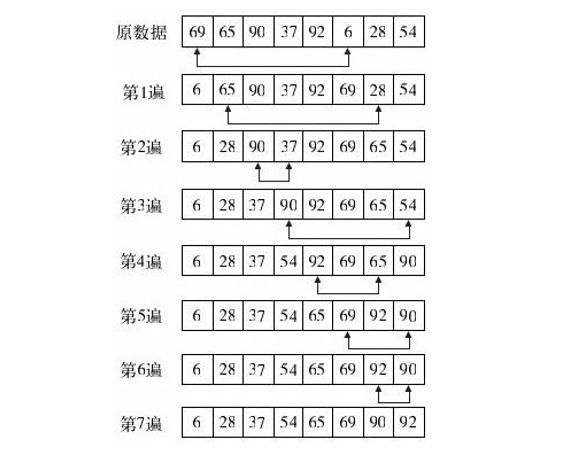
代码实现:
// 选择排序:相邻两个元素进行比较,把大的元素的下标记录下来,一轮完整的比较之后,若最大值的下标不是len-i,则两个元素交换位置
void selectSort(int arr[],int len) {
for(int i=0; i<len; i++) { // 总共要找len-1次最大值,每次找最大值的区间 [0,len-i]
int index_nmax = 0;
for(int j=1; j<len-i; j++) { // 因为假设了0下标就是最大值,所以循环可以从1开始
if(arr[j] > arr[index_nmax]){
index_nmax = j;
}
}
if(index_nmax != len-i-1) {// 避免无意义的位置交换
int tmp = arr[index_nmax];
arr[index_nmax] = arr[len-i-1];
arr[len-i-1] = tmp;
}
}
}
时间复杂度:O((n^2)) 空间复杂度:O(1)
堆排序(大顶堆 、小顶堆 )
利用完全二叉树的结构来维护的一维数组
创建最大堆 :

堆排序(每次取最大值与叶子节点互换移除掉最大元素) :

归并排序
先分后归(先拆分为一个个有序的子序列,再将一个个有序子序列进行归并操作最后合并为一个有序的序列)
流程图:

复杂度
| 算法 | 最好情况 | 平均情况 | 最坏情况 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
分配排序
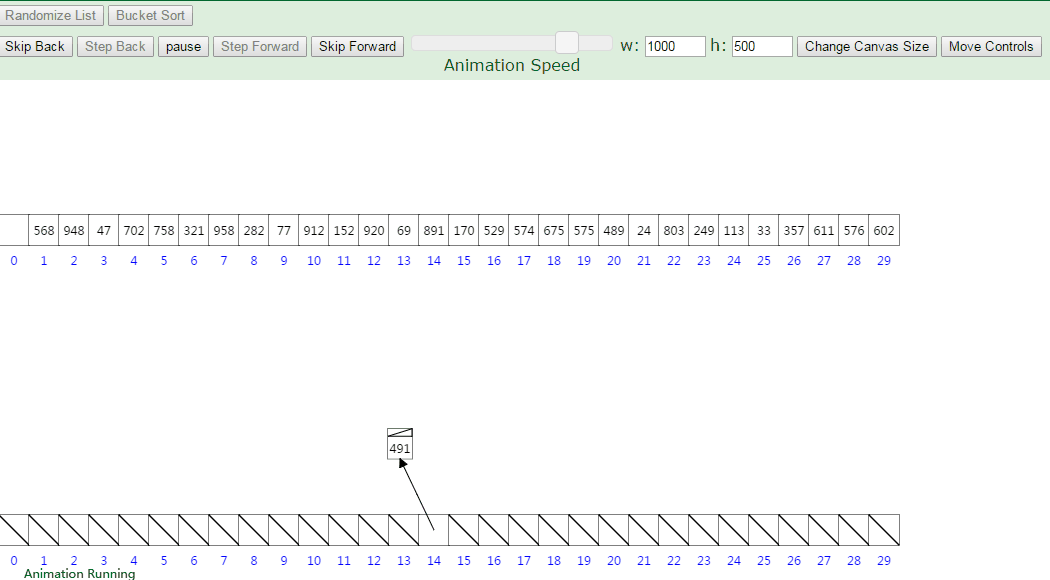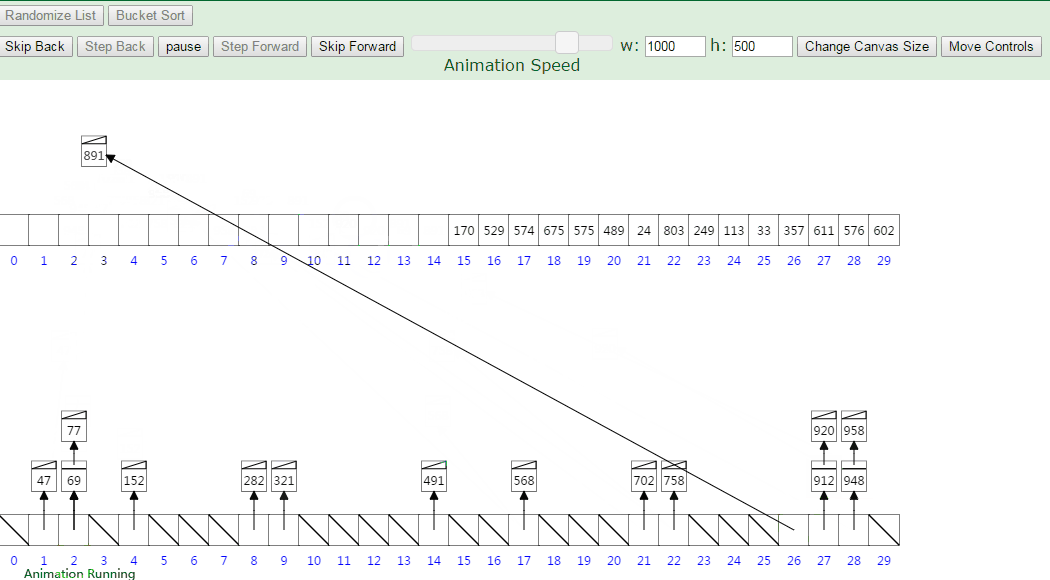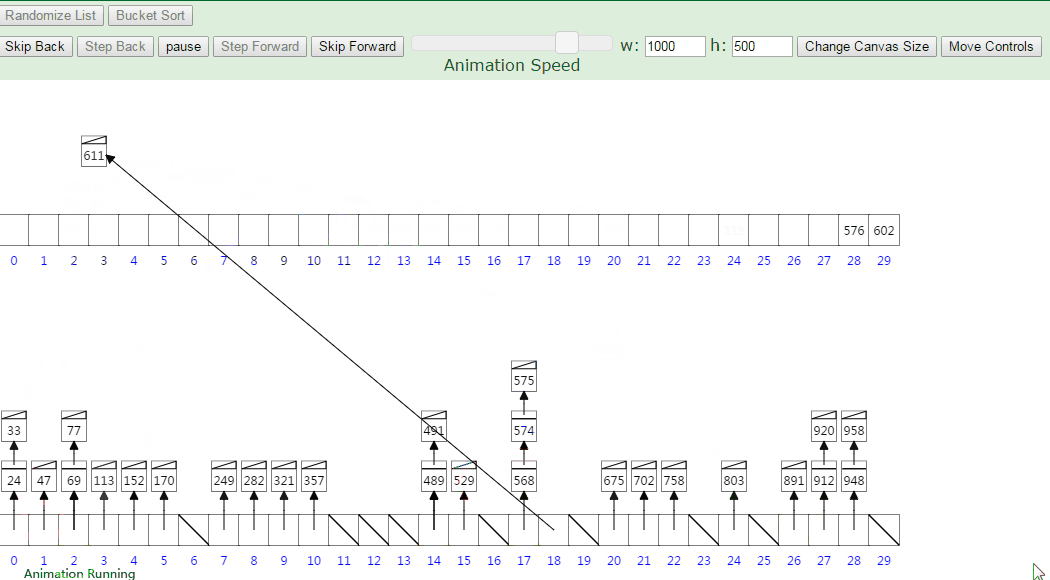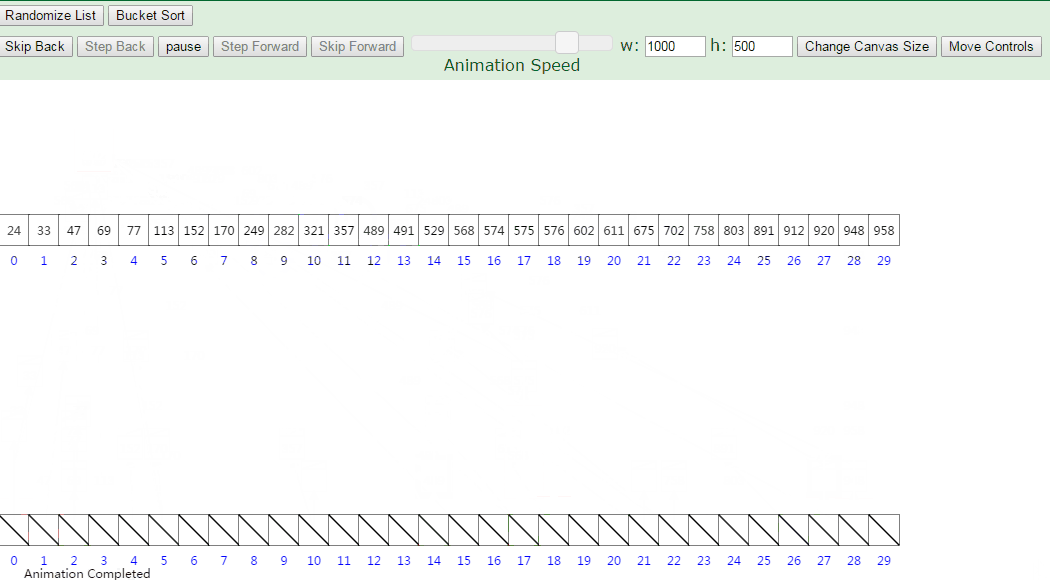
箱排序(桶排序)
流程图:
基数排序(分配和收集 )
(1)假设有欲排数据序列如下所示:
73 22 93 43 55 14 28 65 39 81
首先根据个位数的数值,在遍历数据时将它们各自分配到编号0至9的桶(个位数值与桶号一一对应)中。
分配结果(逻辑想象)如下图所示:
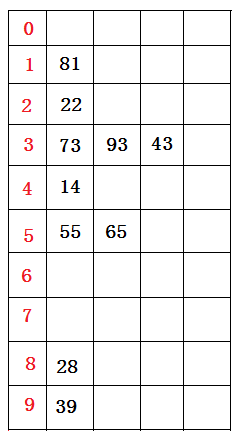
分配结束后。接下来将所有桶中所盛数据按照桶号由小到大(桶中由顶至底)依次重新收集串起来,得到如下仍然无序的数据序列:
81 22 73 93 43 14 55 65 28 39
接着,再进行一次分配,这次根据十位数值来分配(原理同上),分配结果(逻辑想象)如下图所示:
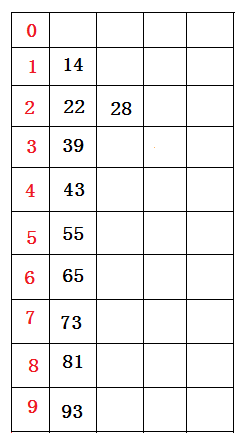
分配结束后。接下来再将所有桶中所盛的数据(原理同上)依次重新收集串接起来,得到如下的数据序列:
14 22 28 39 43 55 65 73 81 93
内部排序的方法比较
时间复杂度
(1)直接插入、直接选择、冒泡排序算法的时间复杂度为O((n^2))
(2)快速、归并、堆排序算法的时间复杂度为O((nlog_{2}n))
(3)希尔排序算法的时间复杂度很难计算:O(n(log_{2}n))或O((n^{1.25}))
(4)基数排序算法的时间复杂度为O(d * (rd+n)),其中rd是基数,d是关键字的位数,n是元素个数。
稳定性
(1)直接插入、冒泡、归并和基数排序算法的稳定的。
(2)直接选择、希尔、快速和堆排序是不稳定的。
辅助空间
(1)直接插入、直接选择、冒泡、希尔和堆排序算法需要辅助空间为O(1).
(2)快速排序算法需要辅助空间为O((log_{2}n))
(3)归并排序算法需要辅助空间为O(n)
(4)基数排序算法需要辅助空间为O(n+rd)