本博客所有内容是原创，未经书面许可，严禁任何形式的转载
http://blog.csdn.net/u010255642
回归分析（英语：Regression Analysis）是一种统计学上分析数据的方法，目的在于了解两个或多个变量间是否相关、相关方向与强度，并建立数学模型以便观察特定变量来预测研究者感兴趣的变量。
回归分析是建立因变量
（或称依变量，反应变量）与自变量
（或称独变量，解释变量）之间关系的模型。简单线性回归使用一个自变量，复回归使用超过一个自变量（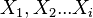
）。
简单的单变量线性回归python实现
#!/usr/bin/env python
# -*- coding: utf-8 -*-
#最小二乘法，单变量线性回归
#麦好myhaspl@qq.com
#http://blog.csdn.net/u010255642/
import matplotlib.pyplot as plt
x =[1,2,3,3,6,12,11]
y =[3,5,8,5,12,26,20]
average_x=float(sum(x))//len(x)
average_y=float(sum(y))/len(y)
x_sub=map((lambda x:x-average_x),x)
y_sub=map((lambda x:x-average_y),y)
x_sub_pow2=map((lambda x:x**2),x_sub)
y_sub_pow2=map((lambda x:x**2),y_sub)
x_y=map((lambda x,y:x*y),x_sub,y_sub)
a=float(sum(x_y))/sum(x_sub_pow2)
b=average_y-a*average_x
plt.xlabel('X')
plt.ylabel('Y')
plt.plot(x, y, '*')
plt.plot([0,15],[0*a+b,15*a+b])
plt.grid()
plt.title("{0}*x+{1}".format(a,b))
plt.show()
