AC自动机真神奇,其实说白了就是在trie树上进行kmp模式匹配,不过刚接触确实有些难度,有些思想确实有些难以理解,所以学习的时候最好亲自手动模拟整个算法的全过程,那我就来写篇blog总结一下。
首先我们需要明白AC自动机是用来干什么的,首先我们知道kmp算法是用来解决单模式串匹配问题的,那么如果模式串不止一个,我们该怎么办呢?没错,AC自动机。我们可以把所有的模式串建立一棵字典树,然后在字典树上进行自我匹配建立next数组,最后利用next数组与主串进行匹配。
建立trie树没有什么问题,最难的地方估计是建立next数组的过程,那我就来手动模拟一下。
假设模式串为:AAAA ABA BBA BBB
主串为:AAAABBABABABB
首先我们建立字典树:
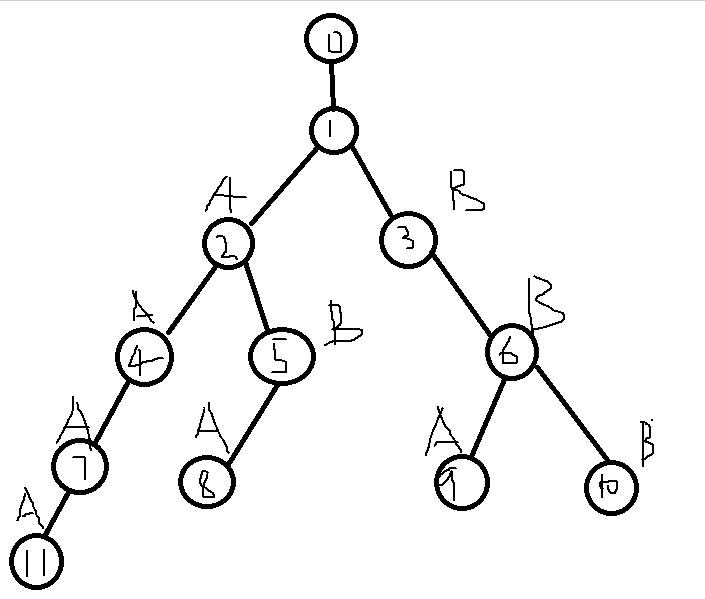
不过AC自动机里的字典树和普通的trie有所不同,这里的trie定义了一个0号虚结点,并且0号结点的所有出边都连向一号点,也就是说我们可以理解为1号结点代表的所有的字符集,然后我们将一号点的next指向0号点。
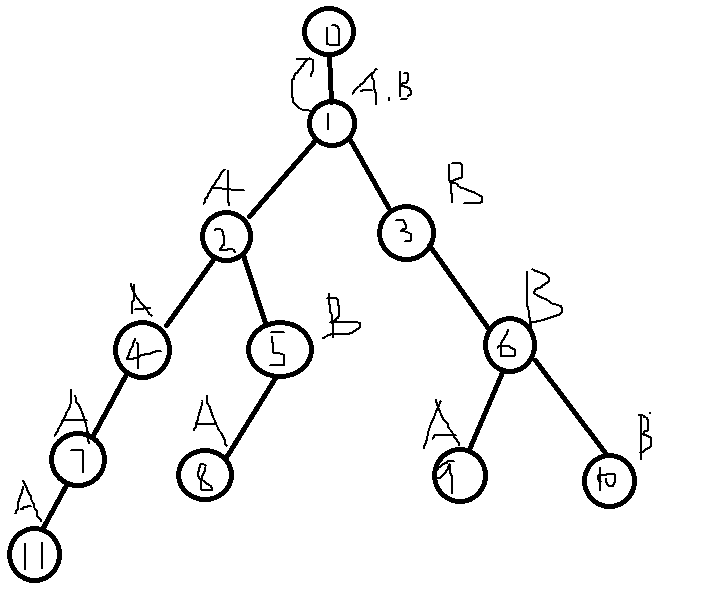
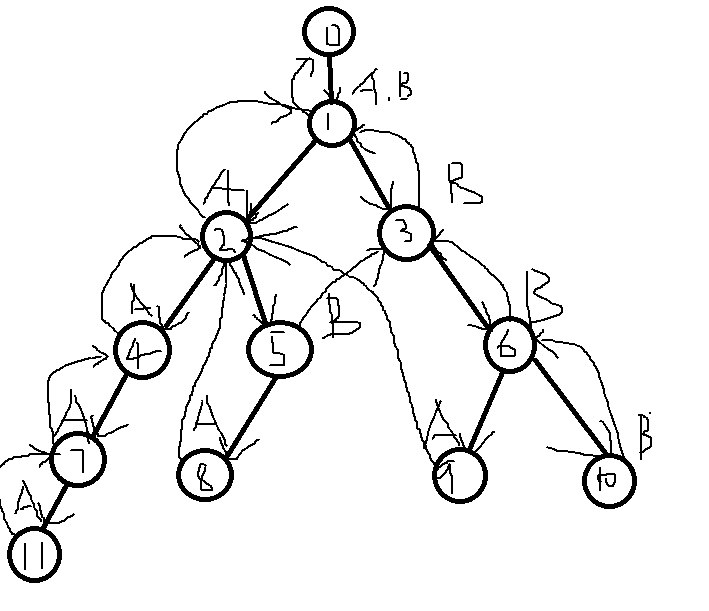
对于2号结点,我们有f[2]=1(其中f[i]表示i结点的父结点)那么我们就看一下1号点的next指向的0号点是否含有A这个儿子。显然1号结点就是这样的结点,所以2号点的next连向1。

同样的我们对于三号点也进行同样的操作,由于一号点的next是0,而0有B这样的儿子,所以把3的next连向1。

对于其余的结点我们也进行一样的操作:
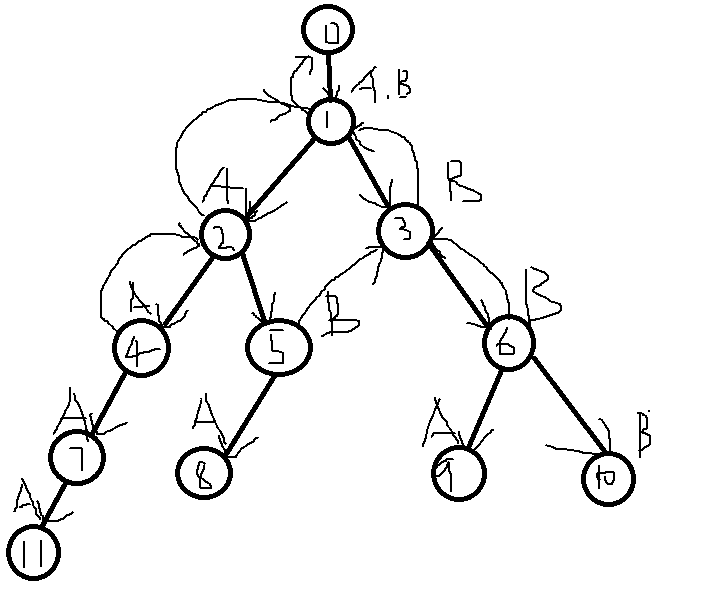
但是对于8号点,它的父亲是5号点,5号点的next为3号点,然而三号点没有A这个儿子结点,那我们就继续查询3号点的next 1号点,一号点有A这个儿子,所以把8号点的next指向2号点。
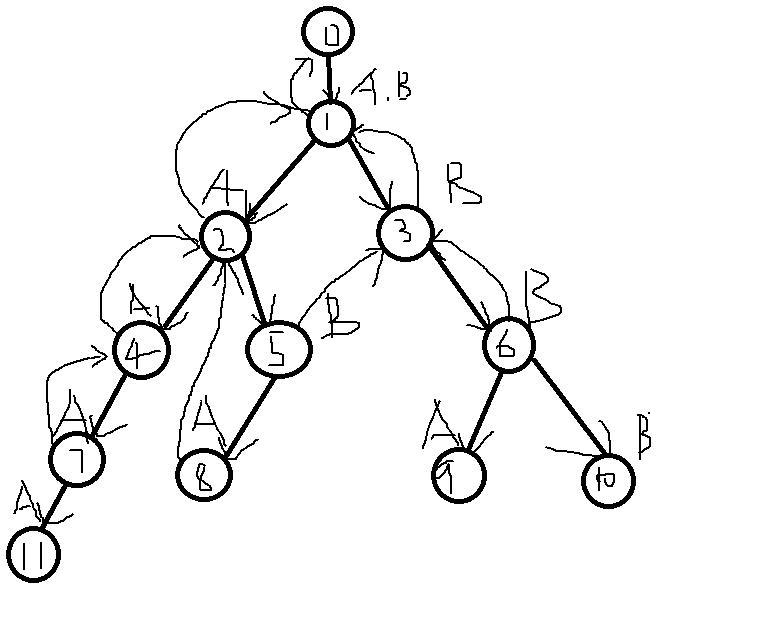
然后我们就可以建立整棵trie树的next数组了。
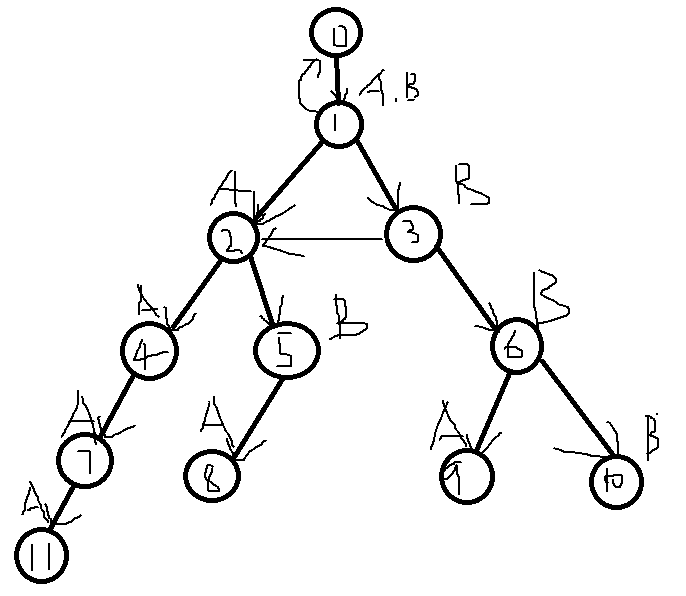
这里有一个问题,我们在询问8号点时,重复跳了几次next这样便使得时间复杂度超过我们期望的O(n),所以我们需要进行一些神奇的操作。

我们在询问三号结点A这个儿子的时候,由于它不存在,一般情况我们就会continue,然后继续询问他的其它儿子,但是我们在询问9号点时,再一次访问了不存在的3号点的A这个儿子,而我们又会继续访问3号点的next所指的结点的A这个儿子,也就是说3号点的A这个儿子在整个操作中完全没有作用但是我们还会重复访问,所以我们就直接把3号点的A儿子直接定义为2号点,也就是next[3]:1的A儿子。这样我们在询问8号点的时候就可以直接将next[9]赋值为9的父结点的next结点的A这个儿子,也就是2号点。这样我们就是实现了O(n)的复杂度来建立next数组。(刚刚接触可能不是很理解,自己多画图模拟就明白了)
建立起next数组后,我们就可以直接让主串在trie树上跑,然后就可以愉快的dp了。

1 void trie(char *s) 2 { 3 int len=strlen(s),u=1; 4 for(int i=0;i<len;i++) 5 { 6 int c=s[i]-'a'; 7 if(!tree[u][c]) 8 { 9 tree[u][c]=++tot; 10 } 11 u=tree[u][c]; 12 } 13 bo[u]++;//记录每个模式串结尾的位置 14 }

1 void bfs() 2 { 3 for(int i=0;i<=25;i++) 4 tree[0][i]=1;//把0的所有出边都设为1 5 next[1]=0;q.push(1);//把1的next记为0,1号点入队 6 while(q.size()) 7 { 8 int u=q.front(); 9 q.pop(); 10 for(int i=0;i<=25;i++) 11 { 12 if(!tree[u][i]) 13 tree[u][i]=tree[next[u]][i];//这里就是上文所述的优化 如果u没有i这个儿子, 14 //那就把next[u]的i这个儿子当做u的i这个儿子 15 else 16 { 17 q.push(tree[u][i]); 18 int v=next[u]; 19 next[tree[u][i]]=tree[v][i]; 20 } 21 } 22 } 23 }

1 void find(char *s) 2 { 3 int u=1,len=strlen(s),k; 4 for(int i=0;i<len;i++) 5 { 6 int c=s[i]-'a'; 7 u=tree[u][c]; 8 } 9 }
接下来是一道模板题:

1 #include<iostream> 2 #include<string> 3 #include<cstdio> 4 #include<cmath> 5 #include<cstring> 6 #include<map> 7 #include<algorithm> 8 #include<stack> 9 #include<queue> 10 #include<vector> 11 #define maxn 1000005 12 using namespace std; 13 14 inline int read() 15 { 16 int x=1,res=0; 17 char c=getchar(); 18 while(c<'0'||c>'9') 19 { 20 if(c=='-') 21 x=-1; 22 c=getchar(); 23 } 24 while(c>='0'&&c<='9') 25 { 26 res=res*10+(c-'0'); 27 c=getchar(); 28 } 29 return res*x; 30 } 31 32 int n,tot=1,ans; 33 char a[maxn]; 34 int tree[maxn][26],next[maxn],bo[maxn]; 35 queue<int>q; 36 37 void trie(char *s) 38 { 39 int len=strlen(s),u=1; 40 for(int i=0;i<len;i++) 41 { 42 int c=s[i]-'a'; 43 if(!tree[u][c]) 44 { 45 tree[u][c]=++tot; 46 } 47 u=tree[u][c]; 48 } 49 bo[u]++; 50 } 51 52 void bfs() 53 { 54 for(int i=0;i<=25;i++) 55 tree[0][i]=1; 56 next[1]=0;q.push(1); 57 while(q.size()) 58 { 59 int u=q.front(); 60 q.pop(); 61 for(int i=0;i<=25;i++) 62 { 63 if(!tree[u][i]) 64 tree[u][i]=tree[next[u]][i]; 65 else 66 { 67 q.push(tree[u][i]); 68 int v=next[u]; 69 next[tree[u][i]]=tree[v][i]; 70 } 71 } 72 } 73 } 74 75 void find(char *s) 76 { 77 int u=1,len=strlen(s),k; 78 for(int i=0;i<len;i++) 79 { 80 int c=s[i]-'a'; 81 k=tree[u][c]; 82 while(k>1&&bo[k]!=-1) 83 { 84 ans+=bo[k]; 85 bo[k]=-1; 86 k=next[k]; 87 } 88 u=tree[u][c]; 89 } 90 } 91 92 int main() 93 { 94 n=read(); 95 for(int i=1;i<=n;i++) 96 { 97 scanf("%s",a); 98 trie(a); 99 } 100 bfs(); 101 scanf("%s",a); 102 find(a); 103 cout<<ans; 104 return 0; 105 }
这还是一道模板题:

1 #include<iostream> 2 #include<string> 3 #include<cstdio> 4 #include<cmath> 5 #include<cstring> 6 #include<map> 7 #include<algorithm> 8 #include<stack> 9 #include<queue> 10 #include<vector> 11 #define maxn 1000005 12 using namespace std; 13 14 struct tr 15 { 16 int next; 17 int vis[26]; 18 int end; 19 int num; 20 }tree[20000]; 21 22 inline int read() 23 { 24 int x=1,res=0; 25 char c=getchar(); 26 while(c<'0'||c>'9') 27 { 28 if(c=='-') 29 x=-1; 30 c=getchar(); 31 } 32 while(c>='0'&&c<='9') 33 { 34 res=res*10+(c-'0'); 35 c=getchar(); 36 } 37 return res*x; 38 } 39 40 int n,tot,ans; 41 char b[155][75]; 42 char a[maxn]; 43 int f[20000]; 44 queue<int>q; 45 46 void trie(char *s,int num) 47 { 48 int len=strlen(s),u=1; 49 for(int i=0;i<len;i++) 50 { 51 int c=s[i]-'a'; 52 if(!tree[u].vis[c]) 53 { 54 tree[u].vis[c]=++tot; 55 } 56 u=tree[u].vis[c]; 57 } 58 tree[u].num=num; 59 } 60 61 void bfs() 62 { 63 for(int i=0;i<=25;i++) 64 tree[0].vis[i]=1; 65 tree[1].next=0;q.push(1); 66 while(q.size()) 67 { 68 int u=q.front(); 69 q.pop(); 70 for(int i=0;i<=25;i++) 71 { 72 if(!tree[u].vis[i]) 73 tree[u].vis[i]=tree[tree[u].next].vis[i]; 74 else 75 { 76 q.push(tree[u].vis[i]); 77 int v=tree[u].next; 78 tree[tree[u].vis[i]].next=tree[v].vis[i]; 79 } 80 } 81 } 82 } 83 84 void find(char *s) 85 { 86 int len=strlen(s),u=1,k; 87 for(int i=0;i<len;i++) 88 { 89 int c=s[i]-'a'; 90 k=tree[u].vis[c]; 91 while(k>1) 92 { 93 f[tree[k].num]++; 94 k=tree[k].next; 95 } 96 u=tree[u].vis[c]; 97 } 98 } 99 100 int main() 101 { 102 while(1) 103 { 104 n=read(); 105 if(n==0) break; 106 memset(tree,0,sizeof(tree)); 107 memset(f,0,sizeof(f)); 108 tot=1;ans=0; 109 for(int i=1;i<=n;i++) 110 { 111 scanf("%s",b[i]); 112 trie(b[i],i); 113 } 114 bfs(); 115 scanf("%s",a); 116 find(a); 117 for(int i=1;i<=n;i++) 118 { 119 ans=max(ans,f[i]); 120 } 121 cout<<ans<<endl; 122 for(int i=1;i<=n;i++) 123 { 124 if(f[i]==ans) 125 printf("%s ",b[i]); 126 } 127 } 128 return 0; 129 }
