线段树优化建边用来处理点与区间和区间与区间之间的连边问题,比如说点u向[2,6]区间内的所有点连一条边,如果一个一个连显然非常麻烦,若是将区间[2,6]像线段树一样拆成log段,那么就可以加快建边速度了。如下图:
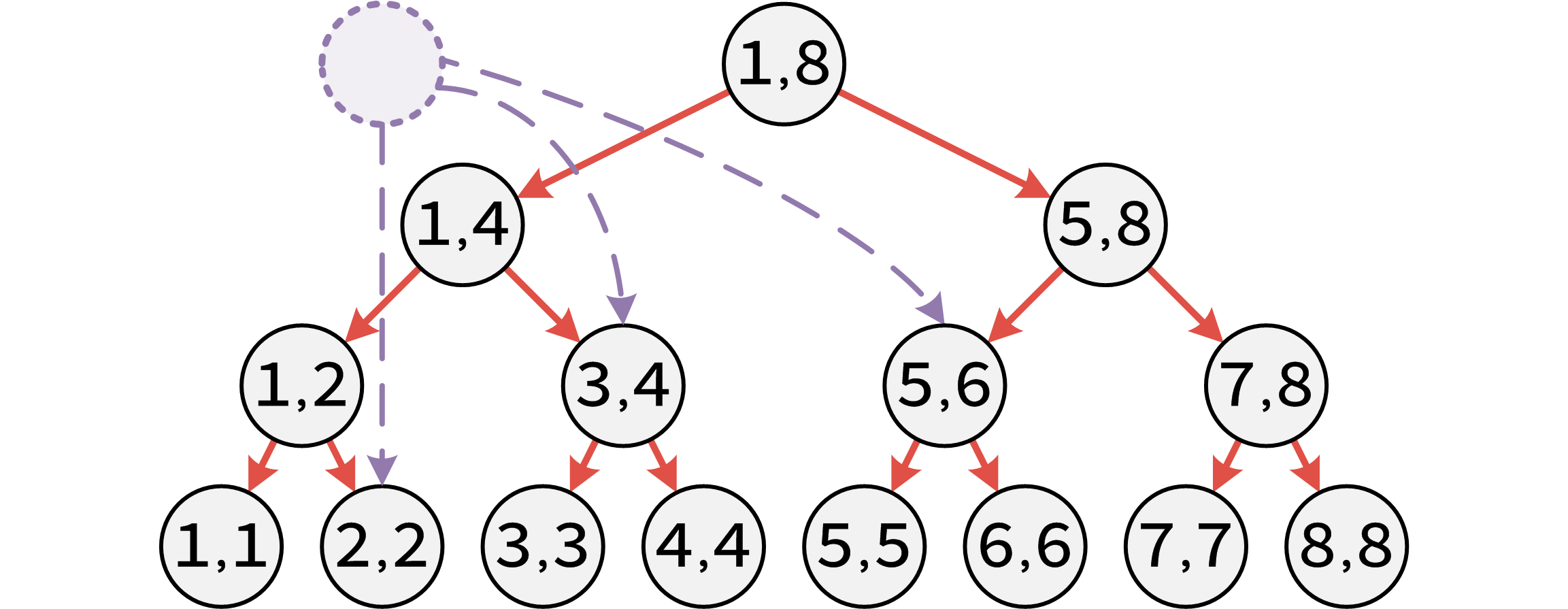
线段树优化建边和线段树的代码差不多,关键就是如何对结点进行编号,首先,为了方便我们要把叶子结点从1到n编号,然后从n+1开始对其他结点依次编号。

1 void build(int &k,int l,int r) 2 { 3 if(l==r) 4 { 5 k=l; 6 return; 7 } 8 k=++cnt;//这里的cnt初值为n。 9 int mid=(l+r)>>1; 10 build(lc[k],l,mid); 11 build(rc[k],mid+1,r); 12 add(k,lc[k],0); 13 add(k,rc[k],0); 14 }
u向[L,R]区间内的所有点连一条边,这和线段树的查找十分类似:

1 void modify(int k,int l,int r,int x,int y,int a,int val)//a向[x,y]中加一条边 2 { 3 if(x<=l&&r<=y) 4 { 5 add(a,k,val); 6 return; 7 } 8 int mid=(l+r)>>1; 9 if(x<=mid) modify(lc[k],l,mid,x,y,a,val); 10 if(mid+1<=y) modify(rc[k],mid+1,r,x,y,a,val); 11 }
这样我们就完成线段树的优化建边了。值得注意的是,线段树内部的结点之间要建边权为0的边。另外如果是[L,R]向一个点连边,那其实也是同样的建树,只不过在线段树上是由子结点向父结点连边:

1 void build2(int &k,int l,int r) 2 { 3 if(l==r) 4 { 5 k=l; 6 return; 7 } 8 k=++cnt;int mid=(l+r)>>1; 9 build2(lc[k],l,mid); 10 build2(rc[k],mid+1,r); 11 add(lc[k],k,0);//这里改为子结点向父结点连边 12 add(rc[k],k,0); 13 } 14 15 void modify2(int k,int l,int r,int x,int y,int a,int val) 16 { 17 if(x<=l&&r<=y) 18 { 19 add(k,a,val);//这里改为子结点向父结点连边 20 return; 21 } 22 int mid=(l+r)>>1; 23 if(x<=mid) modify2(lc[k],l,mid,x,y,a,val); 24 if(mid+1<=y) modify2(rc[k],mid+1,r,x,y,a,val); 25 }
十分easy的线段树优化建边,然后再求一个单源最短路,记得开long long。tips:记得一定要算好空间!

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<string> 5 #include<cmath> 6 #include<queue> 7 #define maxn 10000005 8 #define M 1000005 9 using namespace std; 10 11 int read() 12 { 13 int x=1,res=0; 14 char c=getchar(); 15 while(c<'0'||c>'9') 16 { 17 if(c=='-') 18 x=-1; 19 c=getchar(); 20 } 21 while(c>='0'&&c<='9') 22 { 23 res=res*10+(c-'0'); 24 c=getchar(); 25 } 26 return x*res; 27 } 28 29 struct node{long long d,v;}; 30 struct edge 31 { 32 int next,to,dis; 33 }g[maxn]; 34 priority_queue<node>t; 35 bool operator<(node a,node b){return a.d>b.d;} 36 int n,q,s,e,aa,bb,cc,dd,num,cnt,root1,root2; 37 int last[M],lc[M],rc[M],vis[M]; 38 long long d[M]; 39 40 41 void add(int from,int to,int dis) 42 { 43 g[++num].next=last[from]; 44 g[num].to=to; 45 g[num].dis=dis; 46 last[from]=num; 47 } 48 49 void build1(int &k,int l,int r) 50 { 51 if(l==r) 52 { 53 k=l; 54 return; 55 } 56 k=++cnt;int mid=(l+r)>>1; 57 build1(lc[k],l,mid); 58 build1(rc[k],mid+1,r); 59 add(k,lc[k],0); 60 add(k,rc[k],0); 61 } 62 63 void build2(int &k,int l,int r) 64 { 65 if(l==r) 66 { 67 k=l; 68 return; 69 } 70 k=++cnt;int mid=(l+r)>>1; 71 build2(lc[k],l,mid); 72 build2(rc[k],mid+1,r); 73 add(lc[k],k,0);//这里改为子结点向父结点连边 74 add(rc[k],k,0); 75 } 76 77 void modify1(int k,int l,int r,int x,int y,int a,int val) 78 { 79 if(x<=l&&r<=y) 80 { 81 add(a,k,val); 82 return; 83 } 84 int mid=(l+r)>>1; 85 if(x<=mid) modify1(lc[k],l,mid,x,y,a,val); 86 if(mid+1<=y) modify1(rc[k],mid+1,r,x,y,a,val); 87 } 88 89 void modify2(int k,int l,int r,int x,int y,int a,int val) 90 { 91 if(x<=l&&r<=y) 92 { 93 add(k,a,val);//这里改为子结点向父结点连边 94 return; 95 } 96 int mid=(l+r)>>1; 97 if(x<=mid) modify2(lc[k],l,mid,x,y,a,val); 98 if(mid+1<=y) modify2(rc[k],mid+1,r,x,y,a,val); 99 } 100 101 void dj() 102 { 103 memset(d,127,sizeof(d)); 104 d[s]=0;t.push((node){0,s}); 105 while(t.size()) 106 { 107 int u=t.top().v;t.pop(); 108 if(vis[u]) continue; 109 vis[u]=1; 110 for(int i=last[u];i;i=g[i].next) 111 { 112 int v=g[i].to; 113 if(d[v]>d[u]+g[i].dis) 114 { 115 d[v]=d[u]+g[i].dis; 116 t.push((node){d[v],v}); 117 } 118 } 119 } 120 } 121 122 int main() 123 { 124 n=read();q=read();s=read();cnt=n; 125 build1(root1,1,n); 126 build2(root2,1,n); 127 for(int i=1;i<=q;i++) 128 { 129 e=read(); 130 if(e==1) 131 { 132 aa=read();bb=read();cc=read(); 133 add(aa,bb,cc); 134 } 135 if(e==2) 136 { 137 aa=read();bb=read();cc=read();dd=read(); 138 modify1(root1,1,n,bb,cc,aa,dd); 139 } 140 if(e==3) 141 { 142 aa=read();bb=read();cc=read();dd=read(); 143 modify2(root2,1,n,bb,cc,aa,dd); 144 } 145 } 146 dj(); 147 for(int i=1;i<=n;i++) 148 { 149 if(d[i]>=1e18) printf("-1 "); 150 else printf("%lld ",d[i]); 151 } 152 return 0; 153 }
P3588 [POI2015]PUS
大于关系可以看做是一条边,由较大的数指向较小的数。对于每一个询问,我们考虑让这k个位置上的数与区间内其他的位置两两连有向边。这样一来,问题就转化到图上了。
我们把数列建成一棵线段树,然后对于每个操作区间,它会被k个点割成最多k+1个子区间,对于每个区间,可以化成线段树上的最多log(n)个已知区间,这样我们就需要从已知的k个点向其余的log(n)个点上连边,我们可以新建一个点p,然后k个结点向p连边,p再向其余的点连边,时间复杂度O(klogn),然后拓扑排序判断即可。

1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cstring> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #define maxn 10000005 9 #define M 1000005 10 using namespace std; 11 12 int read() 13 { 14 int x=1,res=0; 15 char c=getchar(); 16 while(c<'0'||c>'9') 17 { 18 if(c=='-') 19 x=-1; 20 c=getchar(); 21 } 22 while(c>='0'&&c<='9') 23 { 24 res=res*10+(c-'0'); 25 c=getchar(); 26 } 27 return x*res; 28 } 29 30 struct edge 31 { 32 int next,to,dis; 33 }g[maxn]; 34 queue<int>q; 35 int n,s,m,root,num,cnt,l,r,k,x,aa,pd; 36 int a[M],last[M],lc[M],rc[M],de[M],dp[M],vis[M]; 37 38 void add(int from,int to,int dis) 39 { 40 g[++num].next=last[from]; 41 g[num].to=to; 42 g[num].dis=dis; 43 last[from]=num; 44 de[to]++; 45 } 46 47 void build(int &k,int l,int r) 48 { 49 if(l==r) 50 { 51 k=l; 52 return; 53 } 54 k=++cnt;//这里的cnt初值为n。 55 int mid=(l+r)>>1; 56 build(lc[k],l,mid); 57 build(rc[k],mid+1,r); 58 add(k,lc[k],0); 59 add(k,rc[k],0); 60 } 61 62 void modify(int k,int l,int r,int x,int y,int a,int val)//a向[x,y]中加一条边 63 { 64 if(x<=l&&r<=y) 65 { 66 add(a,k,val); 67 return; 68 } 69 int mid=(l+r)>>1; 70 if(x<=mid) modify(lc[k],l,mid,x,y,a,val); 71 if(mid+1<=y) modify(rc[k],mid+1,r,x,y,a,val); 72 } 73 74 void topo() 75 { 76 for(int i=1;i<=cnt;i++) 77 { 78 dp[i]=1e9; 79 if(de[i]==0) 80 { 81 q.push(i); 82 if(!a[i]) dp[i]=1e9; 83 else dp[i]=a[i]; 84 } 85 } 86 while(q.size()) 87 { 88 int u=q.front();q.pop();vis[u]=1; 89 for(int i=last[u];i;i=g[i].next) 90 { 91 int v=g[i].to; 92 de[v]--; 93 if(de[v]==0) q.push(v); 94 if(a[v]) 95 { 96 if(a[v]>dp[u]-g[i].dis){pd=1;return;} 97 dp[v]=a[v]; 98 } 99 if(!a[v]) 100 { 101 dp[v]=min(dp[v],dp[u]-g[i].dis); 102 if(dp[v]<=0) {pd=1;return;} 103 } 104 } 105 } 106 for(int i=1;i<=cnt;i++) 107 { 108 if(!vis[i]) pd=1; 109 } 110 } 111 112 int main() 113 { 114 n=read();s=read();m=read();cnt=n; 115 build(root,1,n); 116 for(int i=1;i<=s;i++) 117 { 118 aa=read();a[aa]=read(); 119 } 120 for(int i=1;i<=m;i++) 121 { 122 l=read();r=read();k=read();int pre=l;cnt++; 123 for(int o=1;o<=k;o++) 124 { 125 x=read();add(x,cnt,0); 126 if(pre<=x-1) modify(root,1,n,pre,x-1,cnt,1); 127 pre=x+1; 128 } 129 if(pre<=r) modify(root,1,n,pre,r,cnt,1); 130 } 131 topo(); 132 if(pd) puts("NIE"); 133 else 134 { 135 puts("TAK"); 136 for(int i=1;i<=n;i++) 137 { 138 printf("%d ",dp[i]); 139 } 140 } 141 return 0; 142 }
总结一下,如果我们要从一个点向一段连续的区间上的每一个点都连一条边,那么我们就可以使用线段树优化建边的方法来处理。
