基础实验6-2.6 最短工期 (25分)-拓扑排序

 

 

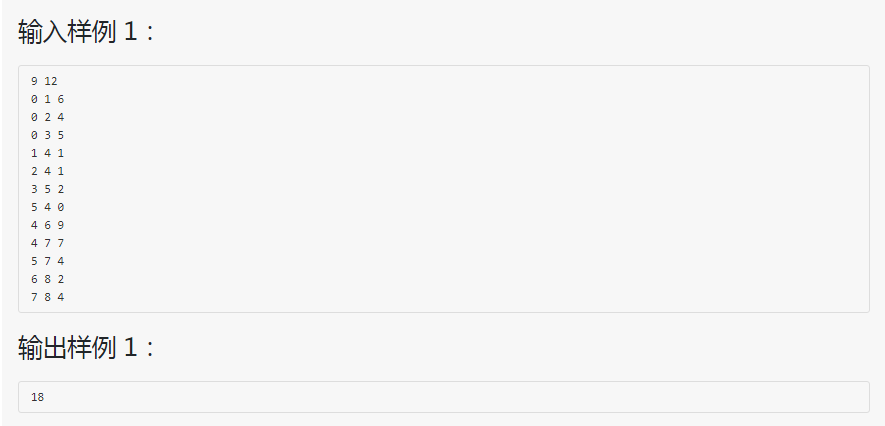
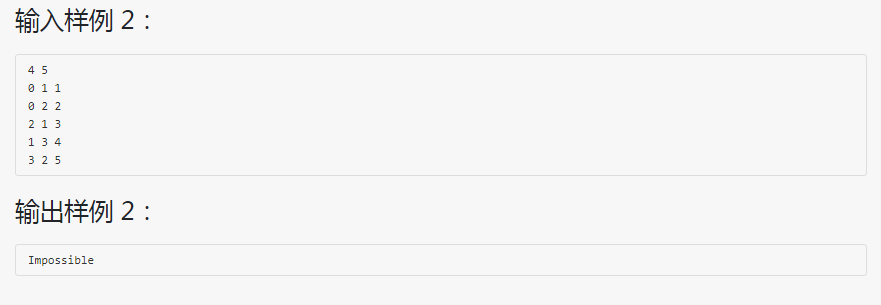
 解题思路：采用拓扑排序思想

#include <stdio.h>
#include <string.h>
#define MaxVex 100
#define INF 0x3f3f3f3f
int G[MaxVex][MaxVex];
int InDegree[MaxVex]= {0};
int time[MaxVex]= {0};
int Nv,Ne;
int ans=0,cnt=0;
int max(int x,int y) {
	return x>y?x:y;
}
void Init() {//图初始化
	memset(G,-1,sizeof(G));
	int i,v1,v2,weight;
	for(i=0; i<Ne; i++) {
		scanf("%d %d %d",&v1,&v2,&weight);
		G[v1][v2]=weight;
		InDegree[v2]++;
	}
}
void Topo() {//拓扑排序
	int i,j;
	while(1) {
		int flag=0;
		for(i=0; i<Nv; i++) {
			if(!InDegree[i]) {//找到入度为0的结点
				InDegree[i]--;
				flag=1;
				cnt++;//统计入度为0的结点个数
				for(j=0; j<Nv; j++) {
					if(G[i][j]!=-1) {
						InDegree[j]--;//度为0的结点所指向结点的入度减1
						time[j]=max(time[j],time[i]+G[i][j]);//计算从i->j所花的最长路径长度
						ans=max(ans,time[j]);//记录所有路径长度中的最大值（多个起点多个终点）
					}
				}
			}
		}
		if(flag==0)
			break;
	}

}

int main() {
	scanf("%d %d",&Nv,&Ne);
	Init();
	Topo();
	if(cnt==Nv)//所有结点最后的和度均为-1，则存在拓扑排序，反之，则不存在拓扑排序
		printf("%d",ans);
	else
		printf("Impossible");

}