HangOver
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10631 Accepted Submission(s):
4537
Problem Description
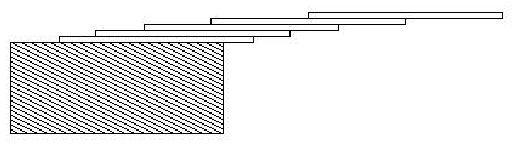
How far can you make a stack of cards overhang a table?
If you have one card, you can create a maximum overhang of half a card length.
(We're assuming that the cards must be perpendicular to the table.) With two
cards you can make the top card overhang the bottom one by half a card length,
and the bottom one overhang the table by a third of a card length, for a total
maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n
cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top
card overhangs the second by 1/2, the second overhangs tha third by 1/3, the
third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table
by 1/(n + 1). This is illustrated in the figure below.
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.
Sample Input
1.00 3.71 0.04 5.19 0.00
Sample Output
1 3 card(s) 2 61 card(s) 3 1 card(s) 4 273 card(s)
Source
//打表找出范围,再遍历;double对应“lf”;
1 #include<stdio.h> 2 double sieve[300]; 3 int main() 4 { 5 int i; double sum=0.0; 6 for(i=1;i<277;i++) 7 { 8 sum+=1.0/(i+1); 9 sieve[i]=sum; 10 } 11 double length; 12 while(~scanf("%lf",&length),length) 13 { 14 for(i=1;i<277;i++) 15 { 16 if(sieve[i]>=length) 17 { 18 printf("%d card(s) ",i); 19 break; 20 } 21 } 22 } 23 return 0; 24 }