线段树优化DP之Monotonicity

题目

P3506 [POI2010]MOT-Monotonicity 2

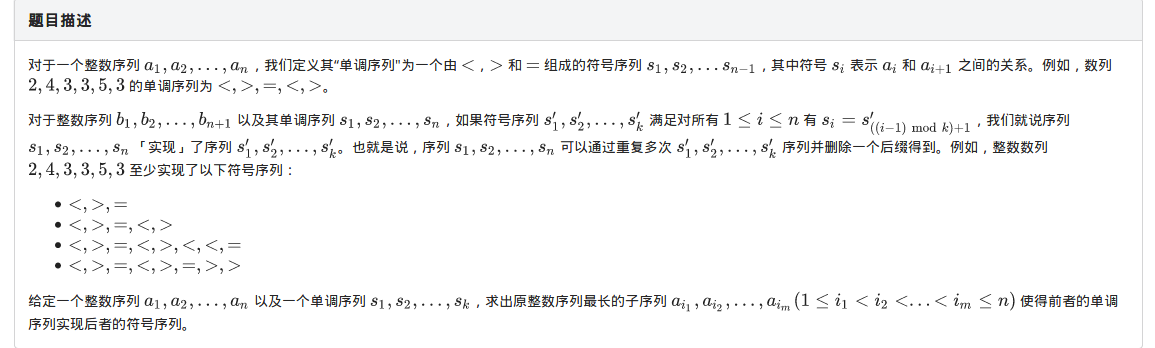
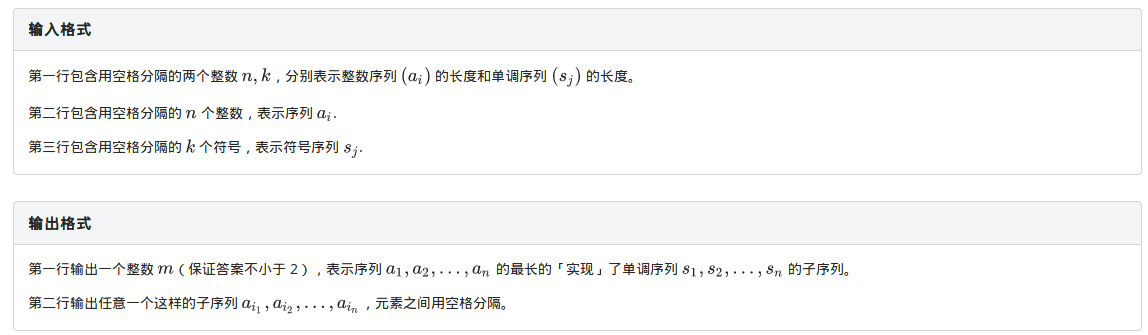
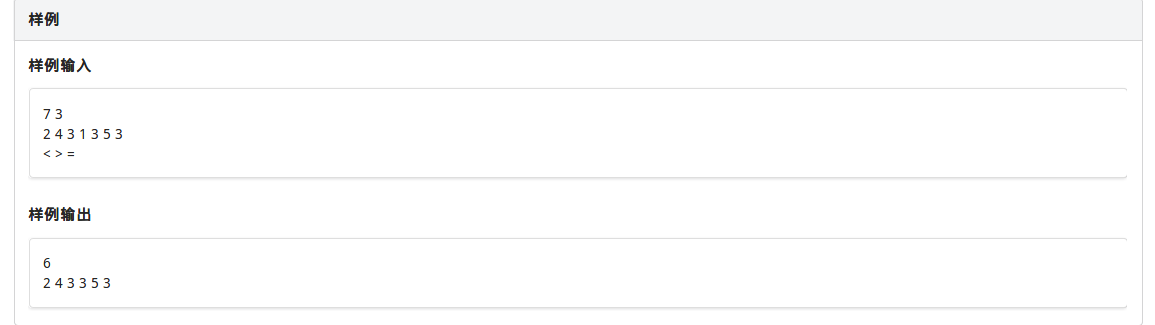
思路

定义f[i]为处理到第i位，所得匹配的最长长度，根据f[i]我们可以求出它后面要跟的符号（可以用符号填满，避免一些取模运算），对于i，我们枚举每一个i前面的j，判断是否合法，那么(n^2)的做法就可以写出来了

#include<bits/stdc++.h>
using namespace std;
const int maxn=20000+10;
int f[maxn],a[maxn];
char op[100+10];
int sta[maxn],top,ans,id;
int path[maxn];
void print(int id){
    if(id==0)return;
    print(path[id]);
    printf("%d ",a[id]);
}
int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1;i<=k;i++){
        scanf(" %c",&op[i]);
    }
    f[1]=ans=id=1;
    for(int i=2;i<=n;i++){
        f[i]=1;
        for(int j=1;j<i;j++){
            char ch=op[(f[j]-1)%k+1];
            if((ch=='>'&&a[j]>a[i])||(ch=='<'&&a[j]<a[i])||(ch=='='&&a[j]==a[i])){
                if(f[i]<f[j]+1){
                    f[i]=f[j]+1;
                    path[i]=j;
                }
            }
        }
    }
    for(int i=1;i<=n;i++){
        if(ans<f[i]){
            ans=f[i];
            id=i;
        }
    }
    printf("%d
",ans);
    print(id);
}

不过根据这道题的数据，(n^2)显然是过不了的，那么我们就考虑优化，所以就有了下面的线段树优化做法

• 维护三棵线段树（貌似两棵也可以），分别维护后面该接 =（root1为根），<（root2为根）, >（root3为根） 的位置
• insert 根据当前的f[i]求出下一个符号该接什么，然后放到相应的线段树里面
  --->后面接”=“, insert(root1,1,1e6,i,f[i]);
  --->后面接“<”, insert(root2,1,1e6,i,f[i]);
  --->后面接“>”, insert(root3,1,1e6,i,f[i]);
• query 分别在三棵线段树中找一个符合情况的最大f[j]（这里就是优化所在，在查找最优j时变成了(log)级别），因为要记录路径，所以我们返回值为位置
  --->在等于的树中取f值最大对应的位置 query(root1,1,1e6,a[i],a[i]);
  --->在小于的树中取f值最大对应的位置 query(root2,1,1e6,1,a[i]-1);
  --->在大于的树中取f值最大对应的位置 query(root3,1,1e6,a[i]+1,1e6);
  对于树上的每一个节点，我们维护tree[i]（f值），pos[i] (在数组中对应的位置)，ls[i] (左儿子)，rs[i] (右儿子),线段树开值域应该比较好维护。

附上代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 10;
int f[maxn * 21], a[maxn];
int nodecnt, root1, root2, root3, ans, id, poss;
int path[maxn], ls[maxn * 21], rs[maxn * 21], tree[maxn * 21], pos[maxn * 21];
char op[maxn];
inline int read() {
    int s = 0, w = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            w = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
    return s * w;
}

void print(int id) {
    if (id == 0)
        return;
    print(path[id]);
    printf("%d ", a[id]);
}
void up(int rt) {
    if (tree[ls[rt]] < tree[rs[rt]]) {
        tree[rt] = tree[rs[rt]];
        pos[rt] = pos[rs[rt]];
    } else {
        tree[rt] = tree[ls[rt]];
        pos[rt] = pos[ls[rt]];
    }
}
void insert(int &rt, int l, int r, int val, int p) {
    if (rt == 0)
        rt = ++nodecnt;
    if (l == r) {
        if (tree[rt] < val) {
            pos[rt] = p;
            tree[rt] = val;
        }
        return;
    }
    int mid = (l + r) >> 1;
    if (a[p] <= mid)
        insert(ls[rt], l, mid, val, p);
    else
        insert(rs[rt], mid + 1, r, val, p);
    up(rt);
    return;
}
int query(int rt, int l, int r, int s, int t) {
    if (l >= s && r <= t)
        return pos[rt];
    if (s > t || !rt)
        return 0;
    int mid = (l + r) >> 1;
    int ans = 0, poss = 0;
    if (s <= mid) {
        int lpos = query(ls[rt], l, mid, s, t);
        if (ans < f[lpos]) {
            ans = f[lpos];
            poss = lpos;
        }
    }
    if (t > mid) {
        int rpos = query(rs[rt], mid + 1, r, s, t);
        if (ans < f[rpos]) {
            ans = f[rpos];
            poss = rpos;
        }
    }
    return poss;
}
int main() {
    int n, k;
    n = read(), k = read();
    for (int i = 1; i <= n; ++i) a[i] = read(), f[i] = 1;
    for (int i = 1; i <= k; ++i) scanf(" %c", &op[i]);
    for (int i = k + 1; i < n; ++i) op[i] = op[(i - 1) % k + 1];
    for (int i = 1, poss; i <= n; ++i) {
        poss = query(root1, 1, 1e6, a[i], a[i]);
	if (f[i] < f[poss] + 1) {
            f[i] = f[poss] + 1;
            path[i] = poss;
        }
        poss = query(root2, 1, 1e6, 1, a[i] - 1);
        if (f[i] < f[poss] + 1) {
            f[i] = f[poss] + 1;
            path[i] = poss;
        }
        poss = query(root3, 1, 1e6, a[i] + 1, 1e6);
        if (f[i] < f[poss] + 1) {
            f[i] = f[poss] + 1;
            path[i] = poss;
        }
        if (ans < f[i]) {
            ans = f[i];
            id = i;
        }
        if (op[f[i]] == '=')
            insert(root1, 1, 1e6, f[i], i);
        else if (op[f[i]] == '<')
            insert(root2, 1, 1e6, f[i], i);
        else if (op[f[i]] == '>')
            insert(root3, 1, 1e6, f[i], i);
    }
    printf("%d
", ans);
    print(id);
    return 0;
}