一、pLSA模型
1、朴素贝叶斯的分析
(1)可以胜任许多文本分类问题。
(2)无法解决语料中一词多义和多词一义的问题——它更像是词法分析,而非语义分析。
(3)如果使用词向量作为文档的特征,一词多义和多词一义会造成计算文档间相似度的不准确性。
(4)可以通过增加“主题”的方式,一定程度的解决上述
问题:一个词可能被映射到多个主题中(一词多义),多个词可能被映射到某个主题的概率很高(多词一义)
2.pLSA模型
基于概率统计的pLSA模型(probabilistic latentsemantic analysis, 概率隐语义分析),增加了主题模型,
形成简单的贝叶斯网络,可以使用EM算法学习模型参数。

(1)D代表文档,Z代表主题(隐含类别),W代表单词;P(d i )表示文档d i 的出现概率, P(z k |d i )表示文档
d i 中主题z k 的出现概率, P(w j |z k )表示给定主题z k 出现单词w j 的概率。
(2)每个主题在所有词项上服从多项分布,每个文档在所有主题上服从多项分布。
(3)整个文档的生成过程是这样的: 以P(d i )的概率选中文档d i ; 以P(z k |d i )的概率选中主题z k ;
以P(w j |z k )的概率产生一个单词w j观察数据为(d i ,w j )对,主题z k 是隐含变量。 (d i ,w j )的联合分布为
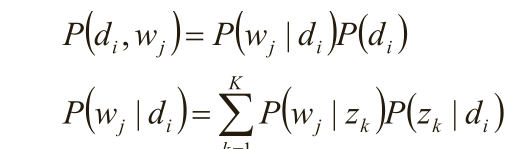
而 对应了两组多项分布,而计算每个文档的主题分布,就是该模型的任务目标。
(4)极大似然估计:w j 在d i 中出现的次数n(di,wj)
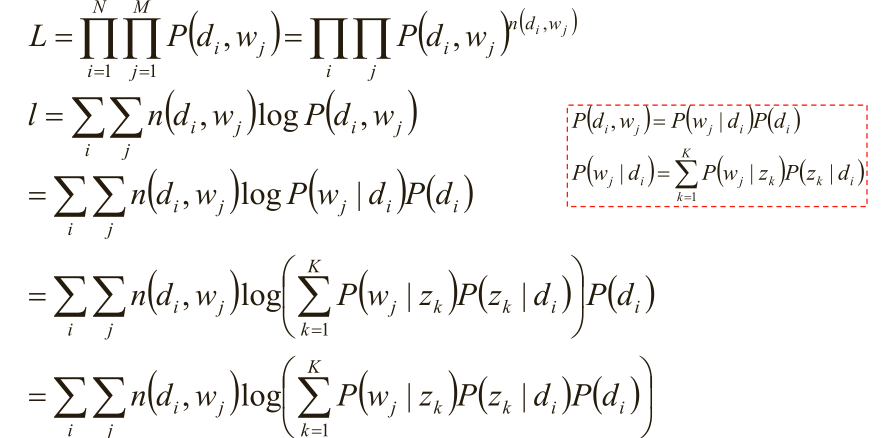
(5)使用逐次逼近的办法:
假定P(z k |d i )、P(w j |z k )已知,求隐含变量z k 的后验概率;
在(d i ,w j ,z k )已知的前提下,求关于参数P(z k |d i )、P(w j |z k )的似然函数期望的极大值,
得到最优解P(z k |d i )、P(w j |z k ) ,带入上一步,从而循环迭代;
隐含变量z k 的后验概率;
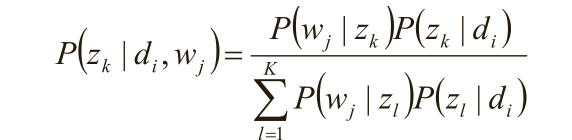
在(d i ,w j ,z k )已知的前提下,求关于参数P(z k |d i )、P(w j |z k ) 的似然函数期望的极大值,得到最优
解P(z k |d i )、P(w j |z k ) ,带入上一步,从而循环迭代;
(6)分析似然函数期望
在(d i ,w j ,z k )已知的前提. 在(d i ,w j ,z k )已知的前提下,求关于参数P(z k |d i )、P(w j |z k ) 的似
然函数期望的极大值,得到最优解P(z k |d i )、P(w j |z k ) ,带入上一步,从而循环迭代
分析似然函数期望:
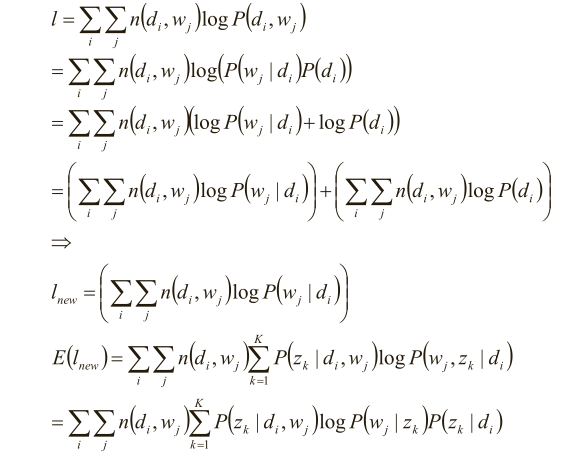
(7)完成目标函数的建立
关于参数P(z k |d i )、P(w j |z k ) 的函数E,并且,带有概率加和为1的约束条件:
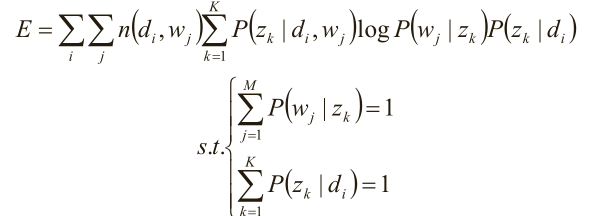
显然,这是只有等式约束的求极值问题,使用Lagrange乘子法解决。
求驻点:
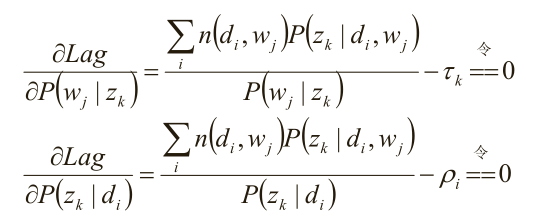
分析第一个等式
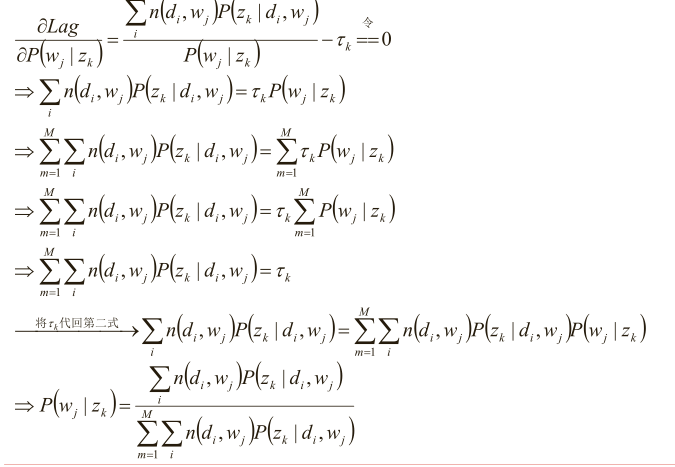
同理分析第二个等式
最后就是下面两步的迭代了,也是实现算法的主要步骤了
求极值时的解——M-Step:
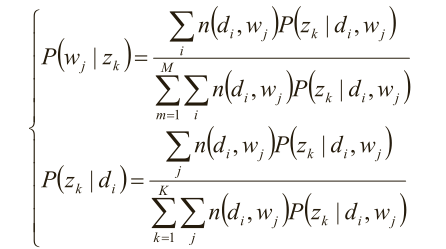
别忘了E-step::

(8)pLSA的总结
1)pLSA应用于信息检索、过滤、自然语言处理等领域,pLSA考虑到词分布和主题分布,使用EM算法来学习参数。
2) 虽然推导略显复杂,但最终公式简洁清晰,很符合直观理解,需用心琢磨;此外,推导过程使用了EM算法,也
是学习EM算法的重要素材。
二、LDA
(1)共轭先验分布
1)由于x为给定样本,P(x)有时被称为“证据”,仅仅是归一化因子,如果不关心P(θ|x)的具体值,只考察θ取何值时
后验概率P(θ|x)最大,则可将分母省去。
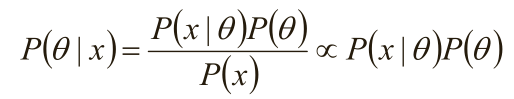
在贝叶斯概率理论中,如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律,那么,先验分布和后验分布被叫做共
轭分布,同时,先验分布叫做似然函数的共轭先验分布。
2)共轭先验分布的实践意义
似然函数P(x|θ)表示以先验θ为参数的概率分布,可以直接求得。 先验分布P(θ)是θ的分布率,可根据先验知识获得。
方案:选取似然函数P(x|θ)的共轭先验作为P(θ)的分布,这样,P(x|θ)乘以P(θ) (然后归一化)得到的P(θ|x)的形式和P(θ)的形式一样。
(2)Dirichlet分布
1) Dirichlet分布的定义:

2)Dirichlet分布分析
α是参数向量,共K个;定义在x 1 ,x 2 …x K-1 维上:x 1 +x 2 +…+x K-1 +x K =1,x 1 ,x 2 …x K-1 >0,
定义在(K-1)维的单纯形上,其他区域的概率密度为0
3)对称Dirichlet分布

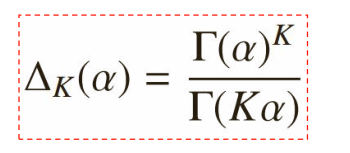
α=1时,退化为均匀分布;
当α>1时, p 1 =p 2 =…=p k 的概率增大
当α<1时, p i =1,p 非i =0的概率增大
(3)LDA的解释
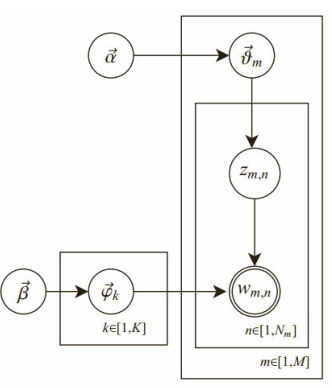
1)共有m篇文章,一共涉及了K个主题;每篇文章(长度为N m )都有各自的主题分布,主题分布是多项分布,该多
项分布的参数服从Dirichlet分布,该Dirichlet分布的参数为α;
每个主题都有各自的词分布,词分布为多项分布,该多项分布的参数服从Dirichlet分布,该Dirichlet分布的参数为 β。
对于某篇文章中的第n个词,首先从该文章的主题分布中采样一个主题,然后在这
个主题对应的词分布中采样一个词。不断重复这个随机生成过程,直到m篇文章全部完成上述过程。
2)参数的学习
给定一个文档集合,w mn 是可以观察到的已知变量,α和β是根据经验给定的先验参数,其他的变量z mn 、θ、φ都
是未知的隐含变量,需要根据观察到的变量来学习估计的。根据LDA的图模型,可以写出所有变量的联合分布:
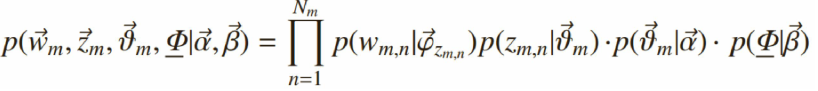
3)似然概率
一个词w mn 初始化为一个词t的概率是:
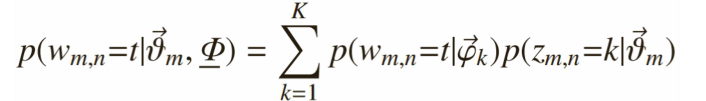
每个文档中出现主题k的概率乘以主题k下出现词t的概率,然后枚举所有主题求和得到。整个文档集合的似然函数为:
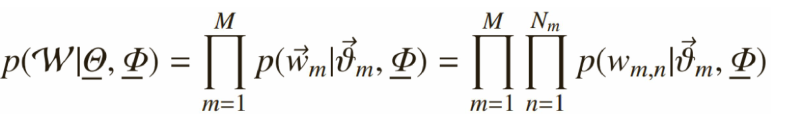
4)Gibbs Sampling
a.Gibbs Sampling算法的运行方式是每次选取概率向量的一个维度,给定其他维度的变量值采样当前维度的值。不断迭代,直到收敛输出待估计的参数。
b.初始时随机给文本中的每个词分配主题z (0) ,然后统计每个主题z下出现词t的数量以及每个文档m下出现主题z的数量,
每一轮计算p(z i |z -i ,d,w),即排除当前词的主题分布:根据其他所有词的主题分布估计当前词分配各个主题的概率。
c.当得到当前词属于所有主题z的概率分布后,根据这个概率分布为该词采样一个新的主题。
d.用同样的方法更新下一个词的主题,直到发现每个文档的主题分布θ i 和每个主题的词分布φ j 收敛,算法停止,
输出待估计的参数θ和φ,同时每个单词的主题z mn 也可同时得出。
e.实际应用中会设置最大迭代次数。每一次计算p(zi|z -i ,d,w)的公式称为Gibbs updating rule。