BSOJ 4490 避难向导

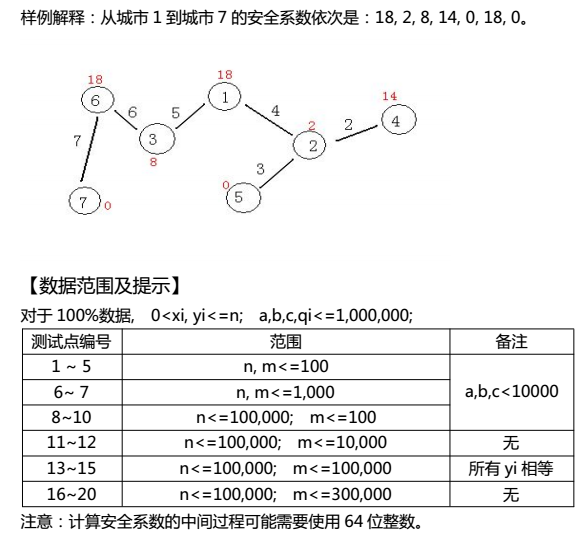
题目大意：树上的每一个节点都有一个d[i]，定义为离最远节点的距离，还有一个s[i]=(d[i]+a)×b%c，再m次询问，每次询问给定(x,y,q)，要求求出(x,y)路径上距x最近的一个点，且满足当前点的s[i]≥q。

emm...这一看就是两道题强行拼起来的，先求出s[i]，然后在处理路径上的询问。

显然对于任意点，距离它最远的点一定是直径的两个端点之一，可以用两次DFS把直径的两端求出来，再把两个距离取个max就行了，算完d[i]后就可以算出s[i]啦。

一看到路径上的询问，我就想起了树剖，但冷静后再想想，这是一道静态问题！直接树上倍增乱搞就行了。

我的思路是这样的：

p[i][j]表示i的第2^k个祖先，g[i][j]表示i到它的第2^k个祖先中s[i]的最大值(不包含i本身)

对于任意一条路径，都可以从LCA(x,y)中拆开(如图)

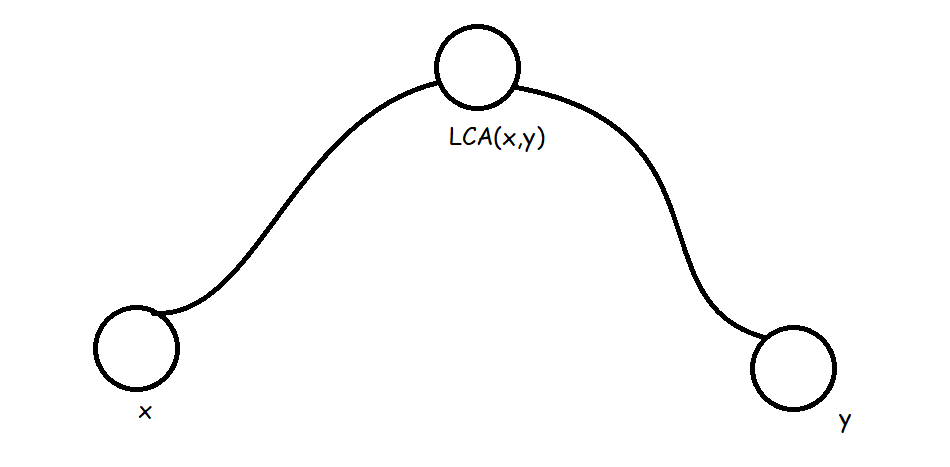
分为两段(x,LCA(x,y))，(LCA(x,y),y)讨论

在(x,LCA(x,y))上时，设Ask(x,k,q)为x到2^k祖先中第一个s[i]≥q的i(不含x)，通过二分的思想：

Ask(x,k,q)=-1  (g[i][k]<q)

Ask(x,k,q)=p[x][0]  (g[i][0]≥q && k=0)

Ask(x,k,q)=Ask(x,k-1,q) 

Ask(x,k,q)=Ask(p[x][k-1],k-1,q)  (Ask(x,k-1,q)=-1)

有了Ask函数之后，再用二进制拆分(x,LCA(x,y))这条链，若找到第一个答案则直接输出，因为在从x往上爬的途中遇到的第一个答案一定是最近的。

在(LCA(x,y),y)上时，同样地，设Ask(x,k,q)为x到2^k祖先中第一个s[i]≥q的i(不含x)：

Ask(x,k,q)=-1  (g[i][k]<q)

Ask(x,k,q)=p[x][0]  (g[i][0]≥q && k=0)

Ask(x,k,q)=Ask(p[x][k-1],k-1,q)

Ask(x,k,q)=Ask(x,k-1,q)  (Ask(p[x][k-1],k-1,q)=-1)

为什么我们的顺序颠倒了，因为在从y往上爬的途中，答案一定是越靠近LCA(x,y)越优的。而且找到第一个答案不能直接输出，因为我们并不知道后面的区间中是否存在答案，如果有的话当前答案完全可以被替代。

最后的询问区间应该长这样

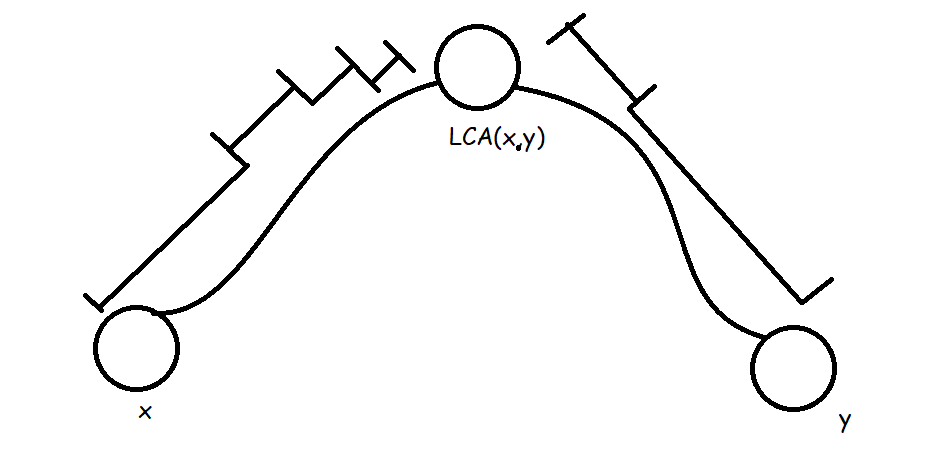
注意：因为g[i][j]是不含i的，所以要在一头一尾加上x和y的特判。

#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define int long long
inline int read() {
    char ch;
    bool bj=0;
    while(!isdigit(ch=getchar()))
        bj|=(ch=='-');
    int res=ch^(3<<4);
    while(isdigit(ch=getchar()))
        res=(res<<1)+(res<<3)+(ch^(3<<4));
    return bj?-res:res;
}
void printnum(int x) {
    if(x>9)printnum(x/10);
    putchar(x%10+'0');
}
inline void print(int x,char ch) {
    if(x<0) {
        putchar('-');
        x=-x;
    }
    printnum(x);
    putchar(ch);
}
const int MAXN=1e5+5;
int n,m,A,B,C,p[MAXN][30],cnt,h[MAXN],g[MAXN][30],log_2[MAXN],dep[MAXN];
int d1[MAXN],d2[MAXN],s[MAXN];
struct Edge {
    int to,nxt,v;
} w[MAXN<<1];
inline void AddEdge(int x,int y,int z) {
    w[++cnt].to=y;
    w[cnt].nxt=h[x];
    w[cnt].v=z;
    h[x]=cnt;
}
void DFS(int x,int fa,int d[],int depth) {
    d[x]=depth;
    for(int i=h[x]; i; i=w[i].nxt) {
        int v=w[i].to;
        if(v==fa)continue;
        DFS(v,x,d,depth+w[i].v);
    }
}
void DFS1(int x,int fa,int depth) {
    p[x][0]=fa;
    g[x][0]=s[fa];
    dep[x]=depth;
    for(int i=h[x]; i; i=w[i].nxt) {
        int v=w[i].to;
        if(v==fa)continue;
        DFS1(v,x,depth+1);
    }
}
inline void Init() {//预处理出d[i]和s[i] 
    int st,ed,maxn=-INF;
    DFS(1,0,d1,0);//从任意节点开始DFS 
    for(int i=1; i<=n; i++)
        if(maxn<d1[i]) {
            maxn=d1[i];
            st=i;//找到直径一端 
        }
    DFS(st,0,d1,0);//从一端DFS
    maxn=-INF;
    for(int i=1; i<=n; i++)
        if(maxn<d1[i]) {
            maxn=d1[i];
            ed=i;//找到直径另一端
        }
    DFS(ed,0,d2,0);//从另一端DFS
    for(int i=1; i<=n; i++) {
        d1[i]=max(d1[i],d2[i]);//取max 
        s[i]=(d1[i]+A)*B%C;
    }
}
inline void ST() {//倍增预处理 
    for(int j=1; j<=log_2[n]; j++)
        for(int i=1; i<=n; i++)
            if(p[i][j-1]) {
                p[i][j]=p[p[i][j-1]][j-1];
                g[i][j]=max(g[i][j-1],g[p[i][j-1]][j-1]);
            }
}
inline int LCA(int x,int y) {//倍增LCA 
    if(dep[x]<dep[y])swap(x,y);
    for(int i=log_2[dep[x]]; ~i; i--)
        if(dep[x]-(1<<i)>=dep[y])x=p[x][i];
    if(x==y)return x;
    for(int i=log_2[dep[x]]; ~i; i--)
        if(p[x][i]&&p[y][i]&&p[x][i]!=p[y][i]) {
            x=p[x][i];
            y=p[y][i];
        }
    return p[x][0];
}
inline int Askx(int x,int k,int q) {//左链的Ask函数，与定义一样 
    if(!k)return g[x][k]>=q?p[x][0]:-1;
    if(g[x][k]>=q) {
        int tmp=Askx(x,k-1,q);
        return tmp!=-1?tmp:Askx(p[x][k-1],k-1,q);
    }
    return -1;
}
inline int Asky(int x,int k,int q) {//同上 
    if(!k)return g[x][k]>=q?p[x][0]:-1;
    if(g[x][k]>=q) {
        int tmp=Asky(p[x][k-1],k-1,q);
        return tmp!=-1?tmp:Asky(x,k-1,q);
    }
    return -1;
}
signed main() {
    n=read();
    m=read();
    A=read();
    B=read();
    C=read();
    for(int i=2; i<=n; i++)log_2[i]=log_2[i>>1]+1;
    int x,y,z;
    for(int i=1; i<n; i++) {
        x=read();
        y=read();
        z=read();
        AddEdge(x,y,z);
        AddEdge(y,x,z);
    }
    Init();
    DFS1(1,0,1);
    ST();
    while(m--) {
        x=read();
        y=read();
        z=read();
        if(s[x]>=z) {//特判x 
            print(x,'
');
            continue;
        }
        int u=LCA(x,y),ans=-1,tmpy=y;
        for(int i=log_2[dep[x]]; ~i; i--)
            if(dep[x]-(1<<i)>=dep[u]) {//二进制拆分 
                ans=Askx(x,i,z);
                if(ans!=-1) {//有答案直接输出 
                    print(ans,'
');
                    break;
                }
                x=p[x][i];
            }
        if(ans!=-1)continue;
        for(int i=log_2[dep[y]]; ~i; i--)
            if(dep[y]-(1<<i)>=dep[u]) {//二进制拆分 
                int r=Asky(y,i,z);
                if(ans==-1||(r!=-1&&dep[r]<dep[ans]))ans=r;//有答案不能直接输出，换成更新当前答案 
                y=p[y][i];
            }
        if(ans==-1)print(s[tmpy]>=z?tmpy:-1,'
');
        else print(ans,'
');
    }
    return 0;
}

时间复杂度：预处理O(nlog n)+单次询问O(log²n)