本文LDA指线性判别模型,并非自然语言处理中的主题模型LDA。
1.LDA简介
LDA在模式识别领域(比如人脸识别等图形图像识别领域)中有非常广泛的应用。LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。如下图

从直观上可以看出,右图要比左图的投影效果好,因为右图的黑色数据和蓝色数据各个较为集中,且类别之间的距离明显。左图实际上是PCA的思想,没有用到类别信息,投影后的方差最大,但分类边界处数据混杂。以上就是LDA的主要思想了,当然在实际应用中,我们的数据是多个类别的,我们的原始数据一般也是超过二维的,投影后的也一般不是直线,而是一个低维的超平面。
LDA除了可以用于降维以外,还可以用于分类。一个常见的LDA分类基本思想是假设各个类别的样本数据符合高斯分布,这样利用LDA进行投影后,可以利用极大似然估计计算各个类别投影数据的均值和方差,进而得到该类别高斯分布的概率密度函数。当一个新的样本到来后,我们可以将它投影,然后将投影后的样本特征分别带入各个类别的高斯分布概率密度函数,计算它属于这个类别的概率,最大的概率对应的类别即为预测类别。(不过LDA似乎很少应用于分类)
2.LDA降维与PCA区别
相同点:
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布。
不同点:
1)LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
从下图形象的看出,在左图数据分布下LDA比PCA降维较优,右图数据分布下,PCA比LDA较优。
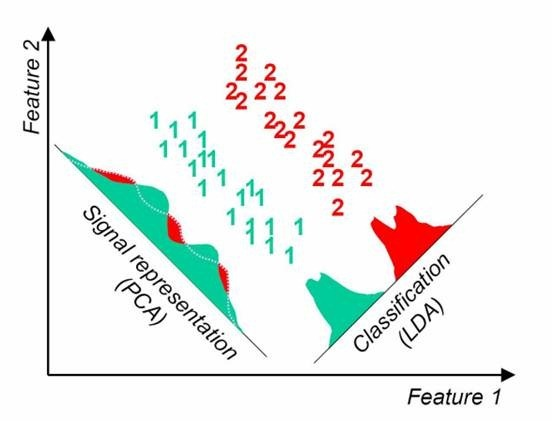
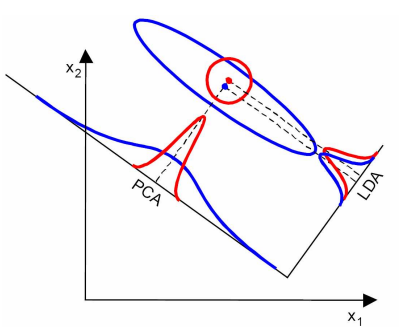
3.LinearDiscriminantAnalysis参数 class sklearn.discriminant_analysis.LinearDiscriminantAnalysis(solver='svd', shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001)
solver:str,求解算法,
取值可以为:
svd:使用奇异值分解求解,不用计算协方差矩阵,适用于特征数量很大的情形,无法使用参数收缩(shrinkage)lsqr:最小平方QR分解,可以结合shrinkage使用eigen:特征值分解,可以结合shrinkage使用
shrinkage:str or float,是否使用参数收缩
取值可以为:priors:array,用于LDA中贝叶斯规则的先验概率,当为None时,每个类priors为该类样本占总样本的比例;当为自定义值时,如果概率之和不为1,会按照自定义值进行归一化None:不适用参数收缩auto:str,使用Ledoit-Wolf lemma浮点数:自定义收缩比例
components:int,需要保留的特征个数,小于等于n-1store_covariance:是否计算每个类的协方差矩阵,0.19版本删除
LinearDiscriminantAnalysis类的fit方法
fit()方法里根据不同的solver调用的方法均为LinearDiscriminantAnalysis的类方法
fit()返回值:
self:LinearDiscriminantAnalysis实例对象
属性Attributes:
covariances_:每个类的协方差矩阵, shape = [n_features, n_features]means_:类均值,shape = [n_classes, n_features]priors_:归一化的先验概率rotations_:LDA分析得到的主轴,shape [n_features, n_component]scalings_:数组列表,每个高斯分布的方差σ
参考:
https://www.cnblogs.com/pinard/p/6244265.html ;
https://blog.csdn.net/qsczse943062710/article/details/75977118