今日学习内容(“显式表达法”更新在Lecture10_几何1(介绍)_GAMES101 课堂笔记中):

第一部分:曲线(Curves)
曲线在建筑设计、动画中三维建模场景中被广泛应用,以及字体中也被广泛应用,因此无论字体多么大,均不会出现锯齿现象。

一、贝塞尔曲线(Bézier Curves)
通过一条多项式曲线,近似表示其控制点。其中,d次曲线,需要 (d+1) 个样本点。
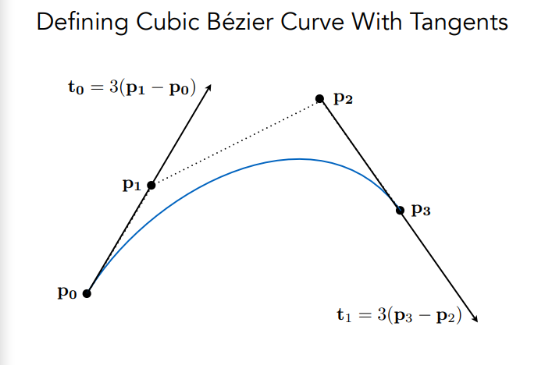
( 一 )de Casteljau算法
de Casteljau算法是比较简单且通用的方法来计算和细分曲线的方法。他通过一系列线性插值计算沿任意次数的贝塞尔曲线的位置。
- de Casteljau原理:
给出任何一个 t ( t 规范到0~1范围内),即可找出 t 时的点的位置。

上图过程解释:
(1)在 (b_0) 与 (b_1) 中找到 (b_0^1)(从起始点 (b_0)开始 t 位置处为(b_0^1)),另外 (b_1) 与 (b_2) 中找到 (b_1^1) (从终止点 (b_2)开始 (1-t) 位置处为(b_1^1))
(2)在 (b_0^1) 与 (b_1^1) 中找到 (b_0^2)(从起始点 (b_0^1)开始 t 位置处为(b_0^2));直到只剩一个点 (b_0^2),因此过程结束。
(3)在 t 从0~1变化过程中,通过上诉递归过程即可画出贝塞尔曲线。
- de Casteljau 过程:
de Casteljau算法首先用直线连接所有相邻的点,然后再直线上找到满足比例 (u) 的点,得到 (n-1) 个点的集合。接着连接这些点,再次按照上述过程对直线进行线性插值,得到 (n-2) 个点的集合。重复这个过程,直到只有一个点。如下图所示:
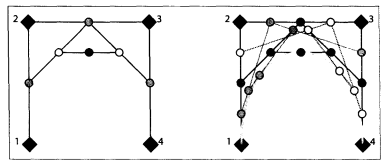
最后拟合曲线结果

递归过程:
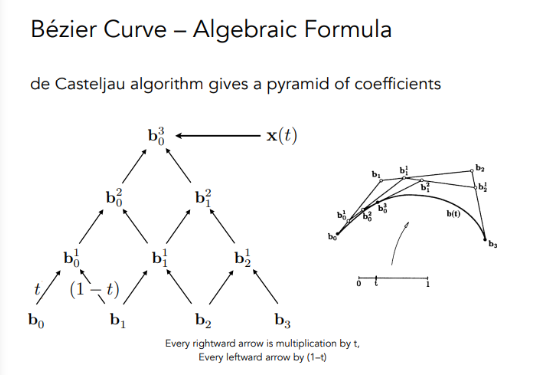
- 贝塞尔曲线通用代式:

-
举例:

-
伯恩斯坦多项式(Bernstein Polynomials)
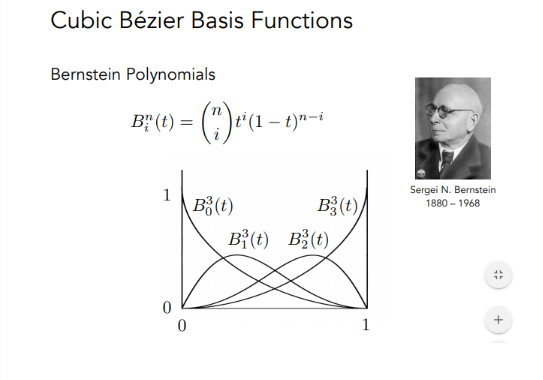
( 二 )贝塞尔曲线性质
其中,强调内容:
-
仿射变换性质:
原始曲线的贝塞尔曲线进行仿射 = 原始曲线的仿射变换曲线的贝塞尔曲线
-
凸包性质:
凸包是指能够包围一系列曲线形体的最小凸多边形。(就好比一个橡皮筋刚好包围多边形)。
该性质是画出的贝尔塞曲线一定在凸包内。

( 三 )分段贝塞尔曲线(Piecewise Bézier Curves)
下图所示的就是分段贝塞尔曲线,由红色的点依次组成的线段拼接而成。
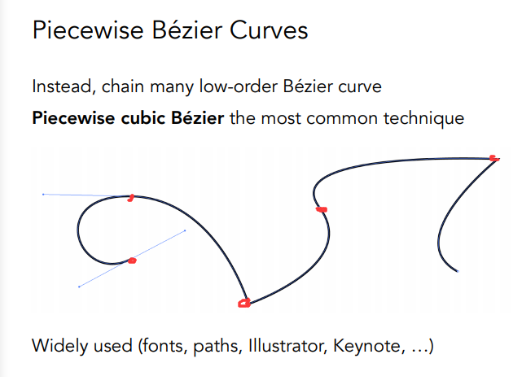
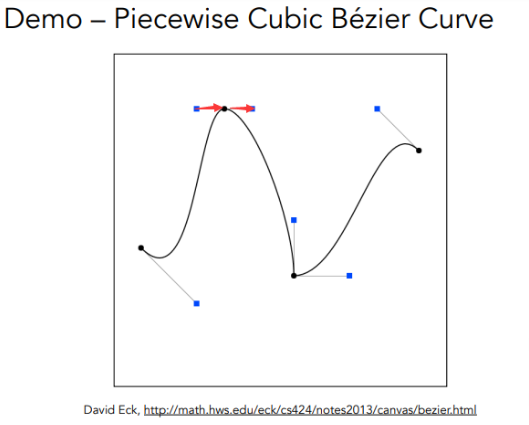
若要使得分段贝塞尔曲线的拼接处光滑(切线光滑),那么要求一阶导数连续(大小、方向均相同),通俗理解是同一个黑色切点的另外两个蓝色点共线、等距。
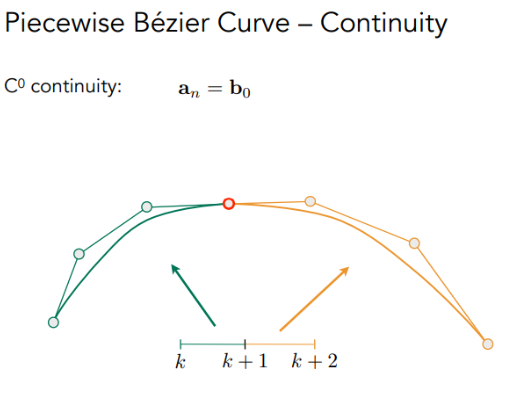
- (C^0连续):(a_n = b_0), 前一段终止点 = 后一段起始点。
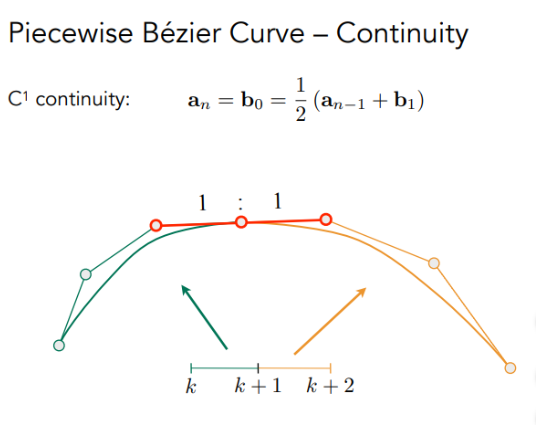
- (C^1)连续:(a_n = b_0 = frac{1}{2}left(a_{n-1} + b_1 ight)),1:1等距相等。
二、样条曲线
所谓样条曲线(Spline Curves)是指给定一组控制点而得到一条曲线,曲线的大致形状由这些点予以控制,一般可分为插值样条和逼近样条两种,插值样条通常用于数字化绘图或动画的设计,逼近样条一般用来构造物体的表面。
B 样条曲线(B-splines)是一种比较常用的样条曲线。连续性的 d 次多项式曲线对 n 个控制点集合进行拟合。
贝塞尔基函数用作权重。B-样条基函数也一样;但更复杂。但是它有两条贝塞尔基函数所没有的特性,即:
(1)定义域被节点细分(subdivided);
(2) 基函数不是在整个区间非零。
实际上,每个B样条基函数在附近一个子区间非零,因此,B-样条基函数相当“局部”。
第二部分:曲面(Surface)

通俗理解:通过对控制点构建贝塞尔曲线,再对贝塞尔曲线上的点求贝塞尔曲线,横竖求解后,即可得到一个平面。
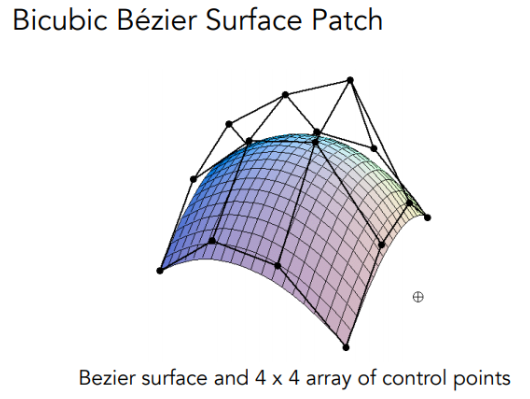
过程可视化:
