P2822 组合数问题

P2822 组合数问题

题目描述

组合数 C_n^mCnm​ 表示的是从 nn 个物品中选出 mm 个物品的方案数。举个例子，从 (1,2,3)(1,2,3) 三个物品中选择两个物品可以有 (1,2),(1,3),(2,3)(1,2),(1,3),(2,3) 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 C_n^mCnm​ 的一般公式：

C_n^m=frac{n!}{m!(n-m)!}Cnm​=m!(n−m)!n!​

其中 n!=1 imes2 imescdots imes nn!=1×2×⋯×n ；特别地，定义 0!=10!=1 。

小葱想知道如果给定 n,mn,m 和 kk ，对于所有的 0leq ileq n,0leq jleq min left ( i, m ight )0≤i≤n,0≤j≤min(i,m) 有多少对 (i,j)(i,j) 满足 C_i^jCij​ 是 kk 的倍数。

输入输出格式

输入格式：

第一行有两个整数 t,kt,k ，其中 tt 代表该测试点总共有多少组测试数据， kk 的意义见问题描述。

接下来 tt 行每行两个整数 n,mn,m ，其中 n,mn,m 的意义见问题描述。

输出格式：

共 tt 行，每行一个整数代表所有的 0leq ileq n,0leq jleq min left ( i, m ight )0≤i≤n,0≤j≤min(i,m) 中有多少对 (i,j)(i,j) 满足 C_i^jCij​ 是 kk 的倍数。

输入输出样例

输入样例#1： 复制

1 2
3 3

输出样例#1： 复制

1

输入样例#2： 复制

2 5
4 5
6 7

输出样例#2： 复制

0
7

说明

【样例1说明】

在所有可能的情况中，只有 C_2^1 = 2C21​=2 是2的倍数。

组合数公式：C(n,k) = C(n-1,k) + C(n-1,k-1)

杨辉三角求组合数代码：

void com(){
    C[0][0]=1;//初始化 
    for(int i=1;i<=n;i++) C[i][0]=1,C[i][i]=1;//边界条件
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; 
        }
    }
}

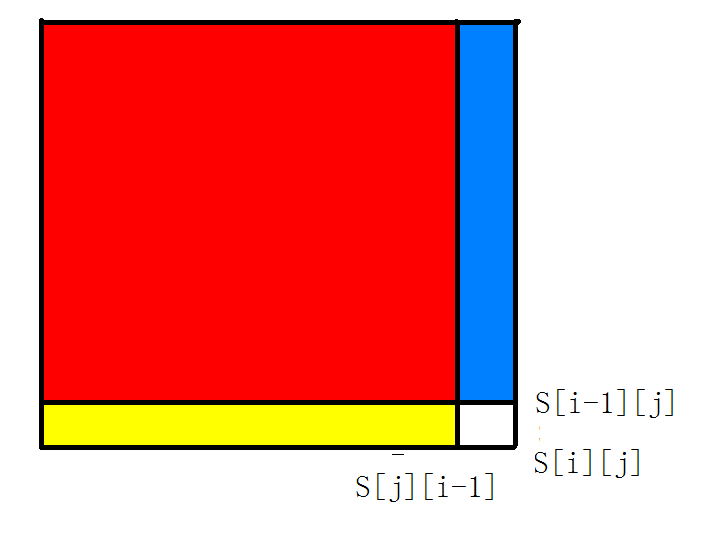
二维前缀和：S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1];

一张图告诉你为何这么做

思路：杨辉三角求组合数，二维前缀和统计答案

#include<iostream>
#include<cstdio>

#define N 5005
using namespace std;

int n,m,C[N][N],S[N][N],k,t;

void com(){
    C[0][0]=1;//初始化 
    n=2000;
    for(int i=1;i<=n;i++) C[i][0]=1,C[i][i]=1;//边界条件
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%k; 
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1];
            if(C[i][j]==0) ++S[i][j];
        }S[i][i+1]=S[i][i];
    }
}

int main()
{
    scanf("%d%d",&t,&k);
    com();
    for(int i=1;i<=t;i++){
        scanf("%d%d",&n,&m);
        if(m>n) m=n;
        printf("%d
",S[n][m]);
    }
    return 0;
}