算法（Algorithms）第4版 练习 1.3.11

主要思路：

这个和Dijkstrad的双栈算法不太一样，后缀的计算只需要一个栈即可。

用一个栈来存数字栈即可。

遇到数字，压栈。

遇到运算法，从栈中弹出相应的数字，用该运算法计算得到结果。

再次压入栈中。

最终从栈中弹出最终运算结果。

方法实现：

//1.3.11
//only support +-*/ operator
package com.qiusongde;

import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;

public class EvaluatePostfix {

    public static void main(String[] args) {
        Stack<Double> vals = new Stack<Double>();
        
        while(!StdIn.isEmpty()) {
            
            String s = StdIn.readString();
            
            if(s.equals("+")) {
                double v = vals.pop();//second operand
                v = vals.pop() + v;
                vals.push(v);
            }
            else if(s.equals("-")) {
                double v = vals.pop();//second operand
                v = vals.pop() - v;
                vals.push(v);
            }
            else if(s.equals("*")) {
                double v = vals.pop();//second operand
                v = vals.pop() * v;
                vals.push(v);
            }
            else if(s.equals("/")) {
                double v = vals.pop();//second operand
                v = vals.pop() / v;
                vals.push(v);
            }
            else {
                vals.push(Double.parseDouble(s));
            }
            
        }
        
        StdOut.println(vals.pop());
        
    }

}

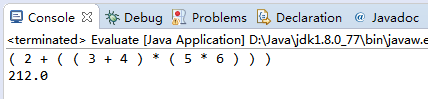
测试1：( 2 + ( ( 3 + 4 ) * ( 5 * 6 ) ) )

用Evaluate计算的结果：

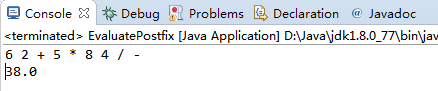
用InfixToPostfix转换结果：

 

用EvaluatePostfix计算的结果：

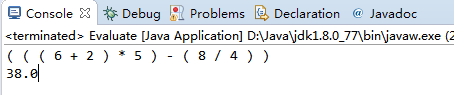
测试2：( ( ( 6 + 2 ) * 5 ) - ( 8 / 4 ) )

 用Evaluate计算的结果：

 

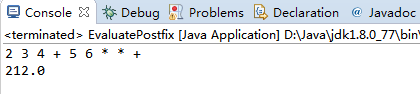
用InfixToPostfix转换结果：

用EvaluatePostfix计算的结果：