Clustering 聚类
Unsupervised learning introduction
supervised learning
在一个典型的监督学习中,我们有一个有标签的训练集,目标是找到能够区分正样本和负样本的决策边界。监督学习中,我们有一系列的标签,需要拟合一个假设函数。
Unsupervised learning
与此不同的是,在无监督学习中,我们的数据没有附带任何标签。我们需要将无标签的训练数据输入到一个算法中,然后告诉这个算法,快去为我们找出这个数据的内在结构。给定数据,我们可能需要某种算法帮助我们寻找一种结构(如将数据分为两组,分开的点集称为簇)。一个能够将这些点集进行分类的算法,就被称为聚类算法,这也是将要介绍的第一个无监督学习算法。
Applications of clustering
- Market segmentation 市场分割(在数据库中存去了许多客户的信息,希望将他们分为不同的客户群,以便于对不同类型客户分别销售产品或提供更适合的服务)
- Social network analysis 社交网络分析(谁经常和谁聊天、谁经常和谁发邮件……由此找到关系密切的人群)
- Organize computing clusters 组织计算机集群或更好管理数据中心(如果知道数据中心哪些计算机经常协作工作,就可以重新分配资源、布局网络,由此优化数据中心、数据通信)
- Astrinomical data analysis 了解星系的行成
K-means algorithm
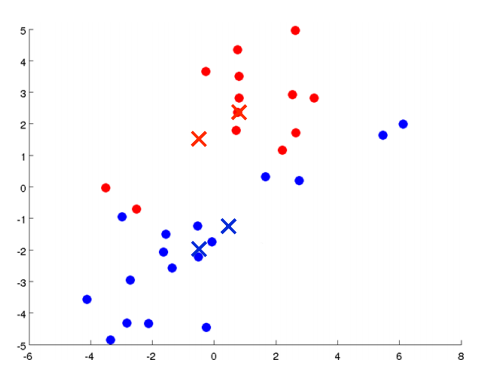
K均值算法最好用图来表达。如下图所示,有一些没加标签的数据,想将这些数据分成两个簇。
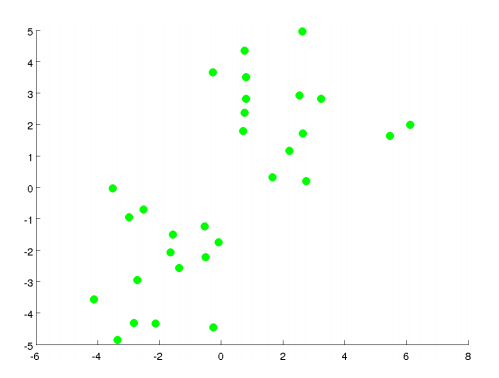
K均值算法是一个迭代算法,它要做两件事:第一是簇分配,第二是移动聚类中心。具体执行K均值算法的过程是这样的:
-
随机选择两个点,这两个点叫做聚类中心。(选两个点是代表希望聚出两个类)

-
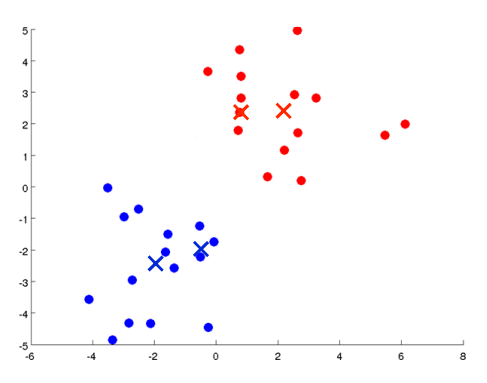
进行簇分配:遍历所有样本,然后依据每一个点是更接近红色的中心还是蓝色的中心来将每个数据点分配到两个不同的聚类中心。(也可看做染色)
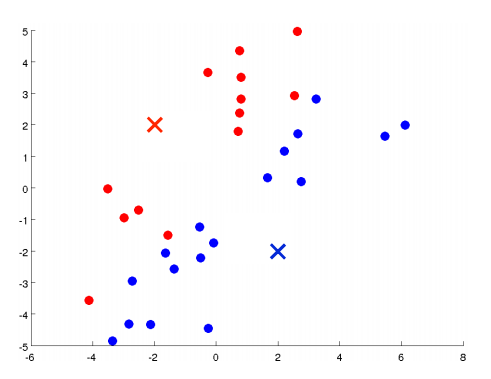
-
移动聚类中心:将两个聚类中心移动到和它一样颜色的那对点的均值处。(均值处是指同一个颜色的所有点平均下来的位置)
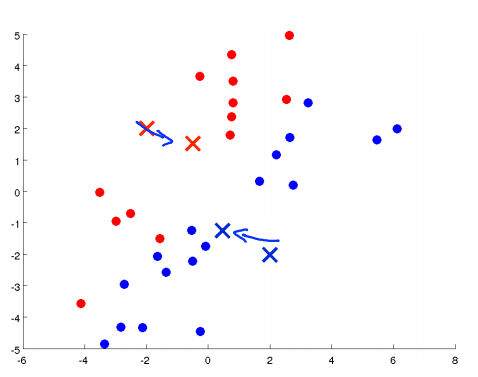
-
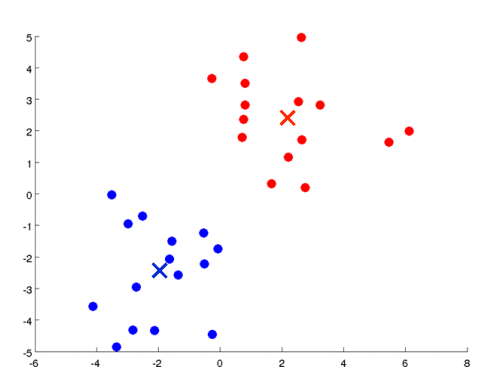
进入下一个簇分配,重复2、3步骤,直到聚类中心不再改变(收敛)。

Input:
- K (number of clusters) 参数K,聚类的数目
- Training set ({x^{(1)},x^{(2)},...,x^{(m)} }) 只有(x)没有(y)的训练集。
(x^{(i)} in R^n) (drop (x_0 = 1) convention) (x^{(i)})是一个(n)维向量
Algorithm
Randomly initialize (K) cluster centroids (mu_1),(mu_2),(dots),(mu_K in R^n)
Repeat {
for (i = 1) to (m)
(c^{(i)}) := index (from (1) to (K)) of cluster centroid closest to (x^{(i)})
for (k = 1) to (K)
(mu_k) := average (mean) of points assigned to cluster (k)
}
K-means for non-separated clusters
应对没有很好分开的簇,如下图所示的例子。
Optimization objective
K-means optimization objective K均值的最优化目标
我们对(c^{(i)})和(u_i)两个变量进行追踪。
-
(c^{(i)}) = index of cluster (1,2,...,K) to which example (x^{(i)}) is currently assigned. 当前样本(x^{(i)})所归属的那个簇的索引或序号
-
(mu_k) = cluster centroid (k) ((mu_k in R^n)). 第(k)个簇的聚类中心
-
(mu_{c^{(i)}}) = cluster centroid of cluster to which example (x^{(i)}) has been assigned. (x^{(i)})所属的簇的聚类中心
最优化目标:找到最小的(c^{(i)})和(u_i),最小化(J(c^{(1)},dots,c^{(m)},mu_1,dots,mu_k) = frac{1}{m}sum_{i=1}^m||x^{(i)}-mu_{c^{(i)}}||^2)
Random initialization
如何避开局部最优化来构建K均值聚类方法。
Should have (K lt m). Randomly pick (K) training examples. Set (u_1,dots,u_K) equal to these (K) examples.
简单粗暴:随机挑选(K)个训练样本设为样本中心。
显然通过这种方法会由于局部最优解的原因,得到不一样的结果,如下所示。

解决方法:多次尝试,选取最优结果。
伪代码:
For (i = 1) to (100) {
Randomly initialize K-means.
Run K-means. Get (c^{(1)},dots,c^{(m)},u_1,dots,u_K).
Compute cost function (distortion) (J(c^{(1)},dots,c^{(m)},mu_1,dots,mu_k))
}
Pick clustering that gave lowest cost (J(c^{(1)},dots,c^{(m)},mu_1,dots,mu_k)).
注:通常情况下,(K)越小,结果稳定性越差,需要多次求解保留最优解。
Choosing the number of clusters
如何选择(K)的值?目前还没有一个好的方法或者能够自动完成这件事的算法,最常用的方法仍然是通过看可视化图或者通过查看聚类算法的输出结果或其它一些东西来手动决定聚类的类别数量。
What is the right value of K?
选择(K)的值很困难的一个原因在于,通常在数据集中有多少个聚类是不容易区分的。下图所示的例子中,有的人可能会看到两个聚类,有的人会看到四个聚类。
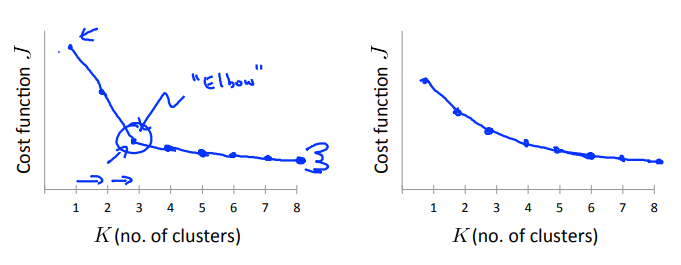
Elbow method: 肘部法则:选取“肘点”
画出失真函数随着(K)的变化情况图:
- 左边的图就明显看出一个“肘点”,在“肘点”左侧,下降的很快,右侧下降的缓慢,此时选取“肘部”的点是正确的。
- 右边的图看不明显的“肘点”,此时无法使用此方法。
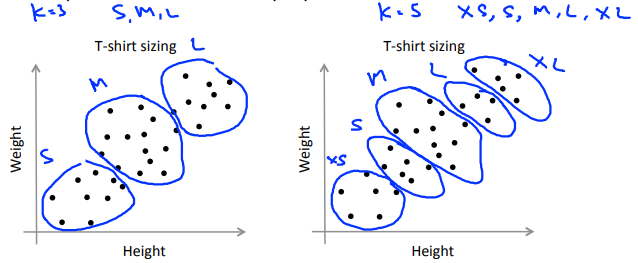
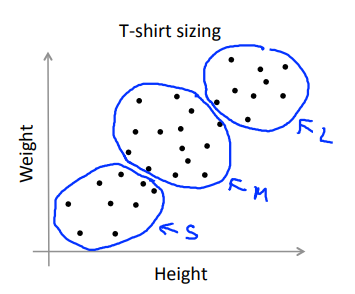
Sometimes, you're running K-means to get clusters to use for some later/downstream purpose. Evaluate K-means based on a metric for how well it performs for that later purpose.
通常人们运行K均值聚类方法时为了得到一些聚类,用于后续操作。也许是用来做市场分割(如上面的T恤尺寸的例子),也许是用来使电脑的聚类变得更好……其中有的会给你一个评估标准,通常,更好的方式是决定聚类的数量,来看不同的聚类数值能为后续目的提供多好的结果。
以T恤尺寸为例,我们尝试决定是否需要3种T恤尺寸。分别算出(K = 3)和(K = 5)的情况,根据实际市场需求决定选取哪种。