二分图的基础定义

二分图又称作二部图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集（A,B），并且图中每条边（i,j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G是一个二分图。
定义

  简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。

辨析

区分二分图，关键是看点集是否能分成两个独立的点集。

 定义
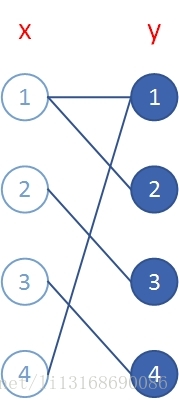
  二分图也称二部图，是图论里的一种特殊模型，也是一种特殊的网络流。其最大的特点在于，可以将图里的顶点分为两个集合，且集合内的点没有直接关联，如下图所示。

理论判断

如果某个图为二分图，那么它至少有两个顶点，且其所有回路的长度均为偶数，任何无回路的的图均是二分图。

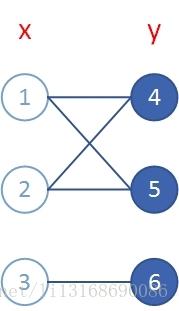
图2

  见图2所示，其存在回路。如：1-4-2-5-1，长度为4，偶数。任意一种都为偶数，证明略。如果在1和2之前添一条边，那就不是二分图了，如图3。 

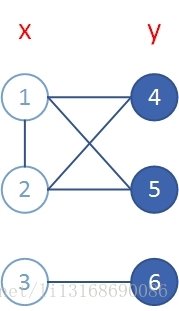
图3

  添了1--2的边后，回路就存在了1--4--2--1，长度为3，奇数，所以图3就不是二分图。

 在绘图时，我发现了一个有趣的现象，当时认为其判定定理有错，后来发现，其实是自己的看法错了，跟大家分享一下。先看下图4，你会发现它存在回路，且任意一种都为偶数，但看上去不像是二分图。

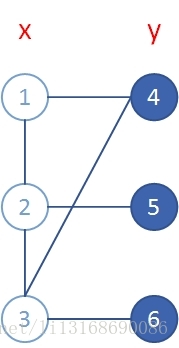
图4

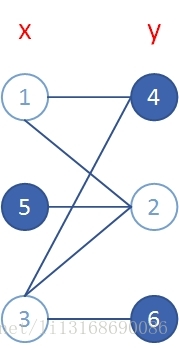
 其实一开始就被这个图给误导了，不用管顶点的颜色，将2和5换个位置，就可以看出来了，见图5。

图5

  如上图所示，将1、5、3分1个集合，4、2、6为1个集合，就是一个二分图。

代码判定

  这里将选用正常的染色法来讲解，

  判断二分图的常见方法是染色法：用两种颜色，对所有顶点逐个染色，且相邻顶点染不同的颜色，如果发现相邻顶点染了同一种颜色，就认为此图不为二分图。 当所有顶点都被染色，且没有发现同色的相邻顶点，就退出。下面有道例题，可以参考一下：

描述 
二部图又叫二分图，我们不是求它的二分图最大匹配，也不是完美匹配，也不是多重匹配，而是证明一个图是不是二部图。证明二部图可以用着色来解决，即我们可以用两种颜色去涂一个图，使的任意相连的两个顶点颜色不相同，切任意两个结点之间最多一条边。为了简化问题，我们每次都从0节点开始涂色 
输入 
输入： 
多组数据 
第一行一个整数 n(n<=200) 表示 n个节点 
第二行一个整数m 表示 条边 
随后 m行 两个整数 u , v 表示 一条边 
输出 
如果是二部图输出 BICOLORABLE.否则输出 NOT BICOLORABLE. 
样例输入 
3 
3 
0 1 
1 2 
2 0 
3 
2 
0 1 
0 2 
样例输出 
NOT BICOLORABLE. 
BICOLORABLE.

邻接矩阵式

#include <iostream>
#include <algorithm>
#include <string.h>
#include <stdio.h>
#include <math.h>
using namespace std;
const int N = 505;
int m,n;
int color[N];
int edge[N][N];
 
bool dfs(int v, int c){
    color[v] = c;    //将当前顶点涂色
    for(int i = 0; i < n; i++){    //遍历所有相邻顶点，即连着的点
        if(edge[v][i] == 1){    //如果顶点存在
            if(color[i] == c)    //如果颜色重复，就返回false
                return false;
            if(color[i] == 0 && !dfs(i,-c))    //如果还未涂色，就染上相反的颜色-c,并dfs这个顶点，进入下一层
                return false;   //返回false
        }
    }
    return true;   //如果所有顶点涂完色，并且没有出现同色的相邻顶点，就返回true
}
 
void solve(){
    for(int i = 0; i < n; i++){
        if(color[i] == 0){
            if(!dfs(i, 1)){
                printf("NOT BICOLORABLE.
");
                return;
            }
        }
    }
    printf("BICOLORABLE.
");
}
 
int main(){
    int u,v;
    while(cin >> n >> m){
        memset(color, 0, sizeof(color));
        memset(edge, 0, sizeof(edge));
        for(int i = 0; i < m; i++){
            cin >> u >> v;    //因为是无向图，所以要往两个方向添加边
            edge[u][v] = 1;    //正着添加
            edge[v][u] = 1;    //反着添加
        }
        solve();
    }
    return 0;
}

领接表式

#include <iostream>
#include <vector>
#include <algorithm>
#include <string.h>
#include <stdio.h>
#include <math.h>
using namespace std;
const int N = 505;
int m,n;
int color[N];
vector<int> node[N];
 
bool dfs(int v, int c){
    color[v] = c;   //为当前顶点上色
    for(int i = 0; i < node[v].size(); i++){    //遍历所有与之连接的顶点，即相邻顶点
       if(color[node[v][i]] == c)   //如果相邻的顶点同色，就返回false
           return false;
        if(color[node[v][i]] == 0 && !dfs(node[v][i], -c))  //如果相邻顶点未染色，就将其染为相反颜色即-c，并继续dfs
           return false;    //返回false
    }
    return true;   //直到所有顶点都被染色，且没出现相邻同色顶点，就返回true
}
 
void solve(){
    for(int i = 0; i < n; i++){     //遍历所有顶点
        if(color[i] == 0){  //如果未染色，就进入深搜
            if(!dfs(i, 1)){
                printf("NOT BICOLORABLE.
");   //如果返回false值，就不是二分图
                return; //结束搜索
            }
        }
    }
    printf("BICOLORABLE.
");   //未出现相邻同色，就是二分图
}
 
int main(){
    int u,v;
    while(~scanf("%d %d",&n,&m)){
        memset(node, 0, sizeof(node));
        memset(color, 0, sizeof(color));
        for(int i = 0; i < m; i++){
            cin >> u >> v;  //因为是无向图，所以要双向插入顶点
            node[u].push_back(v);   //在u点后插入v顶点
            node[v].push_back(u);   //在v点后插入u顶点
        }
        solve();
    }
    return 0;
}