这一节主要讲很多方面非常重要的hash table等问题. 由于平时很少用到这些,基本都忘了。。。
怎样快速的在内存中插入、删除、和搜索呢? 这就需要哈希表了
这一节主要知识点是:1 简单的映射表和处理冲突方法 2.哈希函数的选择 3.开放寻址法(高级解决冲突方案)
1 简单的映射表和处理冲突方法
哈希表希望解决的一个典型问题是编译器内部的符号表,它的结构是:
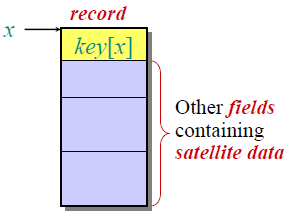
每个记录有一个指针x指向这个记录,key[x]就是这个记录的关键字,然后后面就是一些具体数据。
如果我们想方便得进行增删查操作,这些数据应该如何组织呢?
最简单的方法:直接寻址表
这个方法当键值得范围相对较小的时候还是能够很好工作的。假设key都是从集合U{0,1,..,m-1}中得到的。
则可以建立一个表,T[0.. m-1]
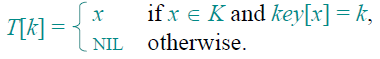
简而言之,这个表就是当k=i时,就将其放在表T中第i个位置。表的其他位置留空就行了:如下图
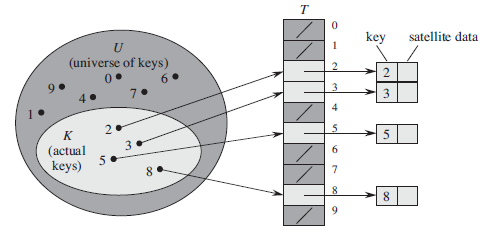
直接寻址法有一个明显的问题,当U的范围很大时,就必须维持一个非常大的表,且实际上用到的可能很少!
而哈希表采用的另一种方法,它通过一个hash函数来映射k值(上面那个方法可以看做identical
mapping的函数)。 但是,这样就会出现不同键映射到相同槽内的方法,那应该怎么处理呢?
这里再给出一个简单方法:通过链表解决
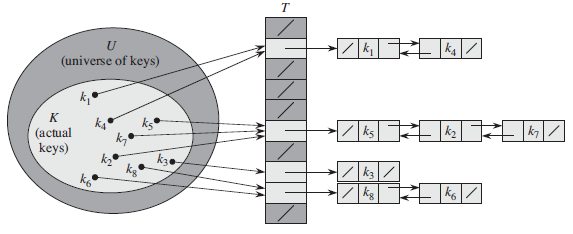
这种方法最差情况就是所有元素都映射到了同一个槽里面,时间就是Θ(n),其实就是建了个链表
下面分析一下平均情况下链表法的性能,顺便引入一些概念:
做假设 哈希函数是简单均匀哈希(simple-uniform hashing),即每个键k 等可能的被hash到表T中的每个槽中,
且与其他键被哈希到什么位置无关
设n是表中key的个数,m是表槽的个数,定义表T的负载因子(load factor):
α = n/m = 平均每个槽中被映射的key的数量
然后给定key后,搜索成功与否的期望时间都是Θ(1+α)
2.哈希函数的选择
怎样选择一个好的hash函数呢?我们期望它具有的性质有下面两点:
- 一个好的hash函数应该能够将keys均匀的映射到表的槽内
- 键值的分布特性应该不影响这种均匀性质
选择的策略主要有两种:除法散列法 乘法散列法
除法散列法: 定义hash函数为 h(k) = k mod m
这种方法也有很多需要注意的: 不要选有很小除数的m. 比如如果选m是个偶数,假设所有的键值都是偶数的情况下,
那么所有的映射结果都只会在偶数槽呢,非常浪费,也违背了上面好的hash函数属性的第二条
另一个极端例子:假设m=2r,就是因子全都是最小的除数。如果k=1011000111011010,r-6,那么映射的结果
就是k的最后6位,这甚至都没有利用k的全部信息
所以这个方法中选择m的原则就是m选为质数且不能太接近2或者10的幂次
乘法散列法:设m=2r, 计算机是w-bit 长的字,然后定义哈希函数是
h(k) = (A*k mod 2w) rsh (w-r)
其中A是一个在(2w-1, 2w)范围内的奇数。
我们来分析这个哈希函数(A*k mod 2w)这一部分就是将乘法得到的结果只取一个字长 ,然后再
rsh w-r位,就刚好只保留了最大是m的结果,可以很好的映射到表中.
假设m=2^3, 字长w是7-bit ,考虑那个乘法过程:
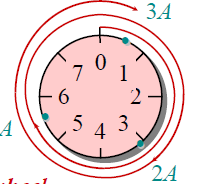
这就像一个幸运大转轮一样,将A转k圈,得到最后的一个结果:
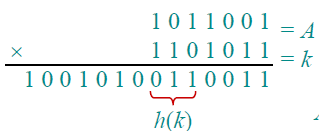
3.开放寻址法
所谓开放寻址法就是没有任何元素时存储在哈希表之外的。 那个当冲突发生时,开放寻址法通过一个探查(Probe)策略不断寻找表中的空槽
探查策略主要包括两种:线性探查 双哈希探查
线性探查使用的哈希函数时:
h(k,i) = (h(k,0)+i)mod m
简单来说,就是原始哈希函数如果映射到一个已经有元素的位置,就直接探查下一个,知道找到空槽。
但是这种方法会出现primary clustering: 某一块会被依次填满,导致映射到那一块时探查时间很长
双哈希探查的哈希函数是:
h(k,i) = (h1(k)+ i*h2(k))mod m
即使用两个哈希函数,当第一次哈希出现冲突时,使用第二个哈希函数做探查,直到找到空槽。
这种方法一般效果很好,但是h2(k)必须和m互质
下面对开放寻址法进行分析:
首先我们假设均匀哈希: 每个key的探查序列等可能的是m!种排列中的任意一种
定理:给定一个开放寻址的哈希表,负载因子α=n/m<1, 则不成功搜索时期望的探查次数最多是1/(1-α)
Proof: 第一次探查是有的,然后发生冲突的概率是n/m,发生冲突后就需要第二次探查了,第二次探查的
概率是(n-1)/(m-1),如此重复下去。
而我们知道n-i/m-1 < n/m =α ,所以我们有 探查的期望次数是:
1+n/m(1+n-1/m-1(1+n-2/m-2(....(1+1/n-m+1)...))
≤ 1+ α(1+α(1+α(...(1+α)...))
≤1+α2+α3+....
=( sum_{i=0}^{INF} alpha^i )
=1/1-α
因为α是常数,则寻址次数也就是一个常数了。但要注意所谓的常数,比如表示半满的,则期望探查此时就是
1/(1-0.5)=2 。 当90%满时,期望探查次数就是1/(1-0.9)=10