关系型数据库的工作原理(一)

本文从"数据库是如何处理一个 SQL 查询的？"这一基本数据库操作来讨论关系数据库的工作原理。

cost based optimization（基于成本的优化）

为了解成本，需要了解一下复杂度的概念，具体考虑时间复杂度，一般用O表示，对应某个算法（查询），对于其随着数据量的增加复杂度增加趋势，而非具体值，O给出了一个很好的描述。时间复杂度一般用最坏时间复杂度表示，除此还有算法内存复杂度，算法I/O复杂度。

归并排序：

归并排序是诸多排序算法中的一种，理解归并排序有助于之后的查询优化以及meger join连接。

归并(merge):

Fig.1

归并排序的大概过程如图1所示：把两个长度为4(N/2)的已排序数组组合成一个有序的长度为8(N)的数组，总计算次数为8(N)，即将两个长度为N/2的数组遍历次数。整个算法可以分为两步：

1. 分解：把整个大数组分解为多个小数组；
2. 排序：几个小数组被（按顺序） 合并起来（使用 merge）构成大数组。

分解：

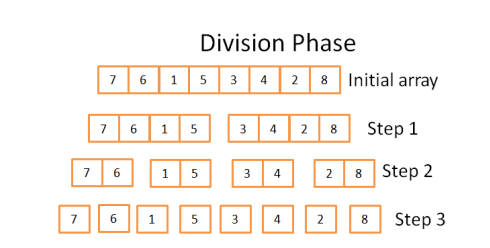
Fig.2

如图2，将N维数组逐层分解为一元数组，分解次数为log(N)。

排序

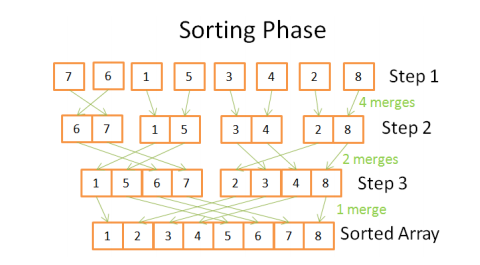
Fig.3

从图3可知，merge的次数与分解的次数是一致的，每次merge对数组元素排序的次数是相同的（N，这里是8）：

Step1: 4次merge，每次对2个元素排序，共4*2次运算。

Step1: 2次merge，每次对4个元素排序，共2*4次运算。

Step1: 1次merge，每次对8个元素排序，共1*8次运算。

故排序的总运算次数为N*log(N)。

算法伪代码：

array mergeSort(array a)

   if(length(a)==1)

      return a[0];

   end if

   //recursive calls

   [left_array right_array] := split_into_2_equally_sized_arrays(a);

   array new_left_array := mergeSort(left_array);

   array new_right_array := mergeSort(right_array);

   //merging the 2 small ordered arrays into a big one

   array result := merge(new_left_array,new_right_array);

   return result;

归并排序的扩展：

1. 在merge 时可以不必创建新数组，而是直接修改原数组，以减少内存，in_place算法即如此。
2. 只对内存中正在处理的数据进行加载从而降低内存和磁盘占用，该类算法为external sorting。
3. 把归并过程在多个进程/线程/服务器上执行，这便是hadoop关键步骤。

    

三种重要的数据结构：

数组

数据库中的表可以理解为数组，如图4：

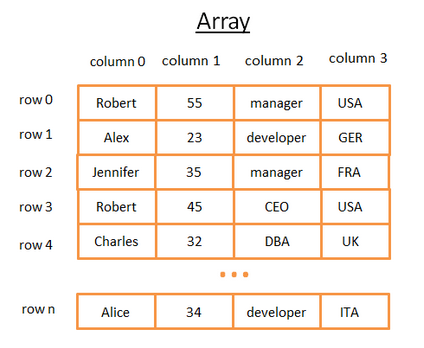
Fig.4

每行代表一个对象；

每列代表一个对象属性，每个属性有一个固定类型(integer, string…)；

二维数组较好的抽象出了数据的存储，但是当对数据进行过滤尤其是有多个过滤条件时，难度非常大，所以用数组抽象数据是不可取的。

树（二叉树/B树）

二叉树是一种特殊树结构，满足一下特点：

左子树在整个对应分支最小，右子树在整个对应分支最大。如图5：

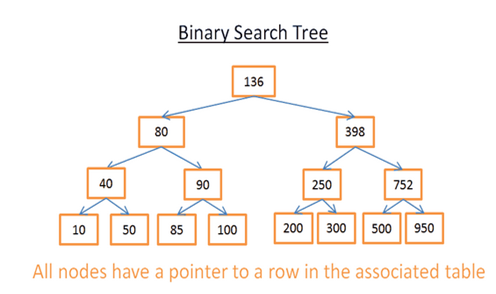
                                 　　　　　　　　　　　　　　　　　　Fig.5        

这是一个简单的B树，共15个节点，如要找40，从根节点136开始，136>40，故查询根节点的左子树80，80>40，再查80的左子树，此时40=40。

对应具体问题，如图4，假设查询某位员工国籍(即column3字段)是UK的，可将国籍作为树节点进行搜索，找到节点值为UK，即可找到UK值所在的行，查询该表中的行，得到其他信息。

B树只需要log(N)次运算，可作为较好的索引搜索，节点存储值的类型可以是多种类型，只要有相应类型的对比函数，就可以进行一次或多次查询过滤。

B+树

B树较好的解决了等值过滤问题，但当出现范围过滤时，就有较大麻烦，比如当要过滤图5中两个值之间数值时，复杂度达N，且为获取整个值不得不加载整个树，增加了I/O。B+树只在最后一层节点才存储数据，其他节点只做路由功能，如图6.

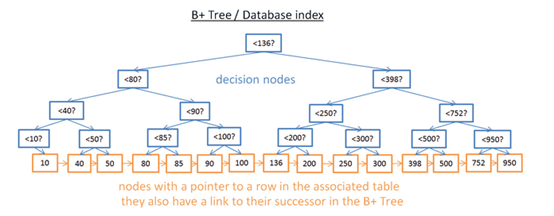
Fig.6

可以看到B+树的每个叶子节点都指向其后续节点，因此当查询t->(M-t)范围内的数据时，复杂度为M+Log(N)，相比B树N，当N很大时，B+树显然速度更快，且因不用遍历整棵树所以I/O很小。

Hash表

哈希表是一种通过元素的key快速查询到数据元素的数据结构，当数据库做查询操作时，通过哈希表更快。哈希表一般有几个部分：

1. 给个元素定义一个key值
2. 定义一个哈希函数，hash函数通过key找到元素位置(bucket)。
3. 定义key值比较函数，通过key值比较函数，在找到的bucket查找对应的值。

                                    　　　　　　　　　　　　Fig.7

如图7，共10个bucket，哈希函数是modulo，比如此时要找59，通过hash函数找到bucket9，然后在bucket9中通过key值对比函数，59!=99，经过7次运算逐值对比发现没有59.

经上列可知，查询复杂度与hash函数相关，hash的值越多(bucket越多)，bucket含有的值越少(key值深度越小)，复杂度越低，但空间占用越大，hash值越小，则相反。如果哈希函数选择得足够好，那么查询的时间复杂度可以是 O(1)。

Hash与数组：

哈希表可以只将部分bucket存入内存（比如常用），其他的Bucket存入磁盘，而数组不得不分配一块连续内存空间，尤其当数组很大时，极困难。

 

----------------------

文章为How does a relational database work笔记，参考其中文翻译Franklin Yang。