关系数据库的工作原理（五）

本篇主要是上篇查询优化例子。

查询优化举例

连接5张表（persons, mobiles, mails, addresses, bank_accounts），获取个人全部信息。

SELECT * from PERSON, MOBILES, MAILS,ADRESSES, BANK_ACCOUNTS
WHERE
PERSON.PERSON_ID = MOBILES.PERSON_ID
AND PERSON.PERSON_ID = MAILS.PERSON_ID
AND PERSON.PERSON_ID = ADRESSES.PERSON_ID
AND PERSON.PERSON_ID = BANK_ACCOUNTS.PERSON_ID

作为查询优化必须解决一下两个问题:

　　1. What kind of join should I use for each join?

　　　　有3种join，且还应考虑是否有索引或者有几个索引，什么类型索引，条件不同，选择的join都会不同。

　　2. What order should I choose to compute the join?

　　　　以下是对四张表的可能的三种连接的顺序情况：

　　　　

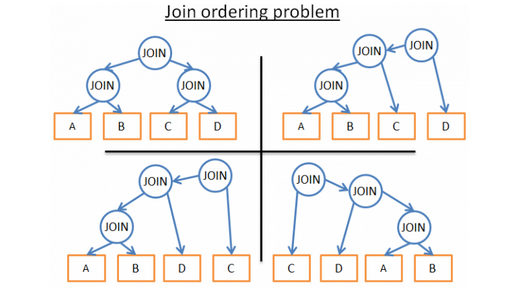
　　　　　　　　　　　　Fig. 14

　　　　 1.暴力寻找

　　　　利用数据库的统计信息，计算每一种查询计划的成本，选择最好的那个计划。但一共有多少种计划呢？对于一种给定顺序的连接，join有三种，那么有3⁴ 种查询计划。而连接顺序本身有(2*4)!/(4+1)!种可能性，则这个查询大概有3⁴ * (2*4)!/(4+1)! 种查询计划。

　　　　2. 利用一些智能规则，（从上面这么多）选取查询计划。查询优化不只是单纯的“找到最优的查询计划”，而是“在有限时间内找到最优的查询计划”。

　　　　多数时候，数据库优化不能找到“最好”的查询计划，而是找到一个“ 还不错” 的。

　　动态规划：

　　对于简单的查询，可以暴力遍历所有查询计划，然后选择一个最优的，对于中型查询，也可以这么做，即动态规划。之所以可以用动态规划，是因为查询中很有查询计划是相似的。

　　　　

　　　　　　　　　　　　Fig. 15

　　从图中可看到，他们都有一个a join b子查询，所以就不需要每次都计算这个子查询的成本，只需计算一次，并将其成本记住，当下次再看到该子查询时直接用即可。其实这就是解决了一个重复计算的问题。使用记忆技术， 所有的查询计划（或者说时间复杂度）不再是(2*N)!/(N+1)!而是3^N。拿我们之前的 4 个表连接的简单例子来说， 所有的查询计划从 336 个减少到 81 个。 如果现在要连接 8 个表（也不算太复杂），意味着所有的查询计划从 57 657 600 减少到 6561。

　　伪代码

procedure findbestplan(S)
if (bestplan[S].cost infinite)
   return bestplan[S]
// else bestplan[S] has not been computed earlier, compute it now
if (S contains only 1 relation)
         set bestplan[S].plan and bestplan[S].cost based on the best way
         of accessing S  /* Using selections on S and indices on S */
     else for each non-empty subset S1 of S such that S1 != S
   P1= findbestplan(S1)
   P2= findbestplan(S - S1)
   A = best algorithm for joining results of P1 and P2
   cost = P1.cost + P2.cost + cost of A
   if cost < bestplan[S].cost
       bestplan[S].cost = cost
      bestplan[S].plan = 『execute P1.plan; execute P2.plan;
                 join results of P1 and P2 using A』
return bestplan[S]

　　对于大型的查询，也可以使用动态规划，但是需要增加附加规则先将明显不好的查询计划去掉：

　　1. 如果分析某一种的查询计划，那其他类型的查询计划就不可以不再考虑，比如只分析left-deep tree，如图16，则只需考虑左上角即可：

　　　　

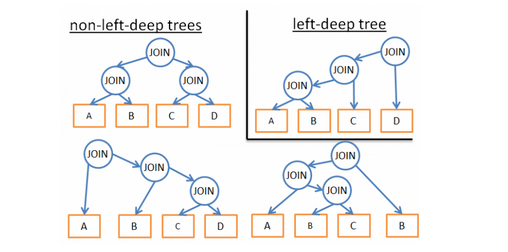
　　　　　　　　　　　　　　　　Fig. 16

　　2.  如果我们再加一个逻辑规则去匹配那些不合适的查询计划然后去掉（比如，“ 如果某个表的某列有索引，而且查询只需要索引列，这样不必尝试 merge join 这个表，而是索引” ） 这样可以显著减少可能查询计划的数量，而且不必担心（因为不大可能） 错失“最好”的查询计划。

　　3. 如果在处理过程逻辑上增加规则（比如，“连接运算符的优先级高于其他运算符”），这样又可以减少一大批（明显不好） 的查询计划。

贪婪算法

    如果对于一个大的查询或者需要一个快速响应（而不需要一个快速查询响应），可以用贪婪算法。

    这个算法的思路是，迭代地使用某一个规则（或者 heuristic，启发）逼近最优的结果。 有了某个规则，贪婪算法可以一步一步地得到最优结果。 这个算法从连接运算符开始处理查询， 然后每一步都使用相同的规则增加一个连接运算符。

    比如，如果我们要在 5 个表（ A， B， C， D 和 E）上做 4 次连接运算。为了简化这个问题， 我们只考虑 nested join 不考虑其他（2 种）连接方式。我们使用“选择成本最低的连接方式”规则：

1. 随机从五张表里选择一个表，比如A
2. 计算其余四张表与A的查询成本（A可以是inner relation或outer relation），比如A JOIN B最低；
3. 分别计算其他三张表与(A JOIN B)查询成本A（(A JOIN B)可以是inner relation或outer relation），比如C JOIN (A JOIN B)最低；
4. 如以上，最后找到以nested join连接的最低成本的连接顺序，比如(((A JOIN B) JOIN C) JOIN D) JOIN E).

　　以上选择了以A为最开始表，再分别以B,C,D,E为开始表，分别计算成本。最后选择一个最低成本的连接方式，即最优查询计划。贪婪算法，如果完整地结合动态规划，时间复杂度大约是 (N*log(N))而不是 (3N)。 如果有一个查询很复杂，需要连接 20次，意味着时间复杂度是 26 而不是 3 486 784 401 那么大。

    贪婪算法是启发式算法类的一种算法，基本思路为保留上一步结果，用于下一步。遗传算法是另一种贪婪算法，在postgres中实现。