谱聚类(Spectral Clustering, SC)在前面的博文中已经详述,是一种基于图论的聚类方法,简单形象且理论基础充分,在社交网络中广泛应用。本文将讲述进一步扩展其应用场景:首先是User-Item协同聚类,即spectral coclustering,之后再详述谱聚类的进一步优化。
1 Spectral Coclustering
1.1 协同聚类(Coclustering)
在数据分析中,聚类是最常见的一种方法,对于一般的聚类算法(kmeans, spectral clustering, gmm等等),聚类结果都类似图1所示,能挖掘出数据之间的类簇规律。
即使对于常见的数据User-Item评分矩阵(常见于各社交平台的数据之中,例如音乐网站的用户-歌曲评分矩阵,新闻网站的用户-新闻评分矩阵,电影网站的用户-电影评分矩阵等等),如表1所示。在聚类分析中,也常常将数据计算成User-User的相似度关系或Item-Item的相似度关系,计算方法诸如应用Jaccard距离,将User或Item分别当成Item或User的特征,再在此基础上计算欧氏距离、cos距离等等。
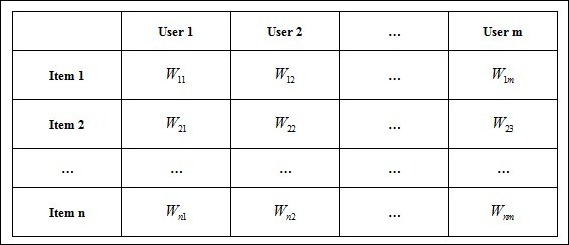
表1 User-Item评分矩阵
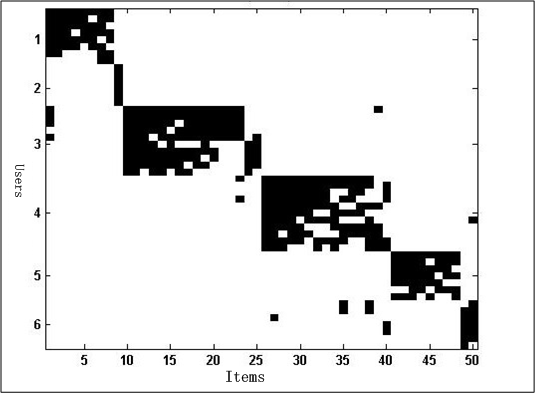
但是如果能聚类成如图2中的coclustering关系,将User和Item同时聚类,将使得数据结果更具意义,即在音乐网站中的用户和歌曲coclustering结果表明,某些用户大都喜欢某类歌曲,同时这类歌曲也大都只被这群用户喜欢着。这样,不管是用于何种场景(例如歌曲推荐),都将带来极大的益处。
1.2 Spectral Coclustering
对于User-Item评分矩阵,这是一个典型的二部图(Bipartite Grap),Item-User矩阵A,假设A为N*M,即N个item和M个user,可展开成:
对于A的二部图,只存在Item与User之间的邻接边,在Item(User)之间不存在邻接边。再用谱聚类原理——将带权无向图划分为两个或两个以上的最优子图,使子图内部尽量相似,而子图间距离尽量距离较远。这样的聚类结果将Cut尽量少的边,分割出User和Item的类,如果类记Ci(U,I)为第i个由特定的User和Item组成的类,由谱聚类原理,Cut掉的Ci边为中的User或Item与其它类Cj(j≠i)的边,且其满足某种最优Cut方法,简单地说,Cut掉的User到其它类Cj(j≠i)的Item的边,可理解为这些User与其它Item相似关系较小;同样Cut掉的Item到其它类Cj(j≠i)的User的边,可理解为这些Item与其它User相似关系较小。这正好满足coclusering的定义。
在谱聚类的基础上,再实现Spectral Coclustering,十分简单, 将E直接当成谱聚类的邻接矩阵即可,至于求Laplacian矩阵、求特征值、计算Kmeans,完成与谱聚类相同。
PS:更多详情,请参见参考文献1。
2 谱聚类的半监督学习
假设有大量新闻需要聚类,但对于其中的部分新闻,编辑已经人工分类好了,例如(Ni1,Ni2, …, Nim),为分类好的第i类,那么对于人工分类好的数据,就相当于聚类中的先验知识(或正则)。
在聚类时,可相应在邻接矩阵E中增加类彼此间邻接边,并使得其邻接权重较大,这样生成的邻接矩阵为E’。这样,再对此邻接矩阵E’做谱聚类,聚类结果将在一定程度上维持人工分类的结果,并达到聚类的目的。
PS:更多详情,请参见参考文献2,不过谱聚类的半监督学习,都有点扯。
参考文献:
1 Inderjit S. Dhillon. Co-clustering documents and words using Bipartite Spectral Graph Partitioning;
2 W Chen. Spectral clustering: A semi-supervised approach;
3 Wen-Yen Chen, Yangqiu Song, Hongjie Bai, Chih-Jen Lin, Edward Y. Chang. Parallel Spectral Clustering in Distributed Systems.
----